01——绪论作业

一.作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述（有理数是其分子、分母均为整数且分母不为零的分数）。
有理数基本运算：

构造有理数T，元素e1,e2分别被赋以分子、分母值
销毁有理数T
用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
有理数T1,T2相加,结果存入有理数T3
有理数T1,T2相减,结果存入有理数T3
有理数T1,T2相乘,结果存入有理数T3
有理数T1,T2相除,结果存入有理数T3

二.实验要求

抽象数据类型名为Rational。
有理数分母不能为负数或者0，类似输入请提示重输入。
数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成，实现用CPP文件完成。Main.cpp文件实现数据输入输出。
数据输入输出格式参考如下：
输入：
1 3 //T1的分子、分母
1 2 //T2的分子、分母
** 输出：**
    5 6  //两个有理数相加
    -1 6  //两个有理数相减
     1 6  //两个有理数相乘
     2 3  //两个有理数相除
程序应对异常输入或者出错必要处理和提示，比如提示：“分数是否需要约分等”。

三.作业内容

1.用ADT抽象数据类型描述有理数抽象数据类型

ADT Rational{

　　数据对象：D={e1,e2|e1,e2均属于ElemType类型}

　　数据关系：R1={<e1,e2>}；R2{<T1,T2>，<T2,T3>};

　　基本操作：

　　　　　　　　int create(int *&R,int e1,int e2);
　　　　　　　　int back(int *R,int &v,int i);
　　　　　　　　int change(int *&R,int v,int i);
　　　　　　　　int destory(int *&R);
　　　　　　　　int add(int v1,int v2,int v3,int v4,int *&R);
　　　　　　　　int subtract(int v1,int v2,int v3,int v4,int *&R);
　　　　　　　　int multiply(int v1,int v2,int v3,int v4,int *&R);
　　　　　　　　int division(int v1,int v2,int v3,int v4,int *&R);

　　}ADT Rational

　　 2.函数说明

1.头文件

2.函数说明

//*****************基本操作函数及说明 ******************
int create(int *&R,int e1,int e2);    
// 操作结果：构造有理数R，分子e1，分母为e2 
int back(int *R,int &v,int i);
// 初始条件：存在有理数T
// 操作结果：用i返回T的分子或者分母值 
int change(int *&R,int v,int i);
// 初始条件：存在有理数T
// 操作结果：改变有理数T的分子或分母值 
int destory(int *&R);
// 销毁有理数T  
int add(int v1,int v2,int v3,int v4,int *&R);
// 操作结果：有理数T1，T2相加，结果存入有理数T3 
int subtract(int v1,int v2,int v3,int v4,int *&R);
// 操作结果：有理数T1，T2相减，结果存入有理数T3 
int multiply(int v1,int v2,int v3,int v4,int *&R);
// 操作结果：有理数T1，T2相乘，结果存入有理数T3 
int division(int v1,int v2,int v3,int v4,int *&R);
// 操作结果：有理数T1，T2相除，结果存入有理数T3 
int reduction(int &v1,int &v2);
// 操作结果：约分函数 
#endif // TRIPLET_H_INCLUDED

3.函数详解

int create(int *&R,int e1,int e2){// 操作结果：构造有理数R，分子e1，分母为e2
    R=new int[2];        //给有理数分配空间存储分子和分母 
    if(!R) exit(-2);    //分配存储空间失败
    R[0]=e1;
    R[1]=e2;
    return 1;
}
int back(int *R,int &v,int i){// 初始条件：存在有理数T
// 操作结果：用i返回T的分子或者分母值 
    if(i<1 || i>2)
        return 0;
    v=R[i-1];
    return 1;
}
int change(int *&R,int v,int i){// 初始条件：存在有理数T
// 操作结果：改变有理数T的分子或分母值 
    if(i<1 || i>2)
        return 0;
    R[i-1]=v;
    return 1;
}
int destory(int *&R){
    free(R);    //释放空间 
    R = NULL;
    return 1;
}
int reduction(int &v1,int &v2){// 操作结果：约分函数 
    int small,s=0;
    if(v1<0){
        v1=-v1;
        s=1;
    }
    if(v1<v2)
        small=v1;
    else 
        small=v2;
    do{                        //找到最小公因数 
        if((v1%small==0)&&(v2%small==0))
            break;
        else
            small--;
    }while(small>=1);
    v1/=small;
    v2/=small;
    if(s==1)
        v1=-v1;
    return 1;
}
int add(int v1,int v2,int v3,int v4)// 操作结果：有理数T1，T2相加，结果存入有理数T3 
{
    int a,b;
    a=v1*v4+v2*v3;
    b=v2*v4;
    if(a==0)
        b=0;
    else
        reduction(a,b);
    cout<<a<<" "<<b<<endl;
}
int subtract(int v1,int v2,int v3,int v4){// 操作结果：有理数T1，T2相减，结果存入有理数T3 
    int a,b;
    a=v1*v4-v2*v3;
    b=v2*v4;
    if(a==0)
        b=0;
    else
        reduction(a,b);
    cout<<a<<" "<<b<<endl;
}
int multiply(int v1,int v2,int v3,int v4)// 操作结果：有理数T1，T2相乘，结果存入有理数T3 
{
    int a,b;
    a=v1*v3;
    b=v2*v4;
    if(a==0)
        b=0;
    else
        reduction(a,b);
    cout<<a<<" "<<b<<endl;
}
int division(int v1,int v2,int v3,int v4)// 操作结果：有理数T1，T2相除，结果存入有理数T3 
{
    int a,b,c=0;
    a=v1*v4;
    b=v2*v3;
    if(a==0)
        b=0;
    
    if(b==0)
        a=0;
    else if(b<0){
        b=-b;
        c=1;
        reduction(a,b);
    }
    else
        reduction(a,b);
    
    if(a<0&&b<0){
        a=-a;
        b=-b;
        c=0;
    }
    
    if(c==0)
    cout<<a<<" "<<b<<endl;
    else
    cout<<-a<<" "<<b<<endl;
}

主函数

int main()
{
    int R1[2],R2[2],R3[2];
    int e,e1,e2;
    int i;    
    int *R=NULL;
    create(R,4,3);
    
    back(R,e,1);
    
    change(R,e,2);
    
    destory(R);
    
    cout<<"输入两个数分别代表R1分子和分母，中间以空格分隔"<<endl;    //在主函数中录入数值 
    do{
        cin>>e1;
        cin>>e2;
        if(e2<=0)
            cout<<"分母不能为负数或者零,请重新输入"<<endl;
        else
            break; 
    }while(1); 
    R1[0]=e1;
    R1[1]=e2;
    reduction(R1[0],R1[1]);
    
    cout<<"输入两个数分别代表R2分子和分母，中间以空格分隔"<<endl;
    do{
        cin>>e1;
        cin>>e2;
        if(e2<=0)
            cout<<"分母不能为负数或者零,请重新输入"<<endl;
        else
            break; 
    }while(1); 
    R2[0]=e1;
    R2[1]=e2;
    reduction(R1[0],R1[1]);
    
    add(R1[0],R1[1],R2[0],R2[1]);
    
    subtract(R1[0],R1[1],R2[0],R2[1]);
    
    multiply(R1[0],R1[1],R2[0],R2[1]);
    
    division(R1[0],R1[1],R2[0],R2[1]);
    
    return 0;
}

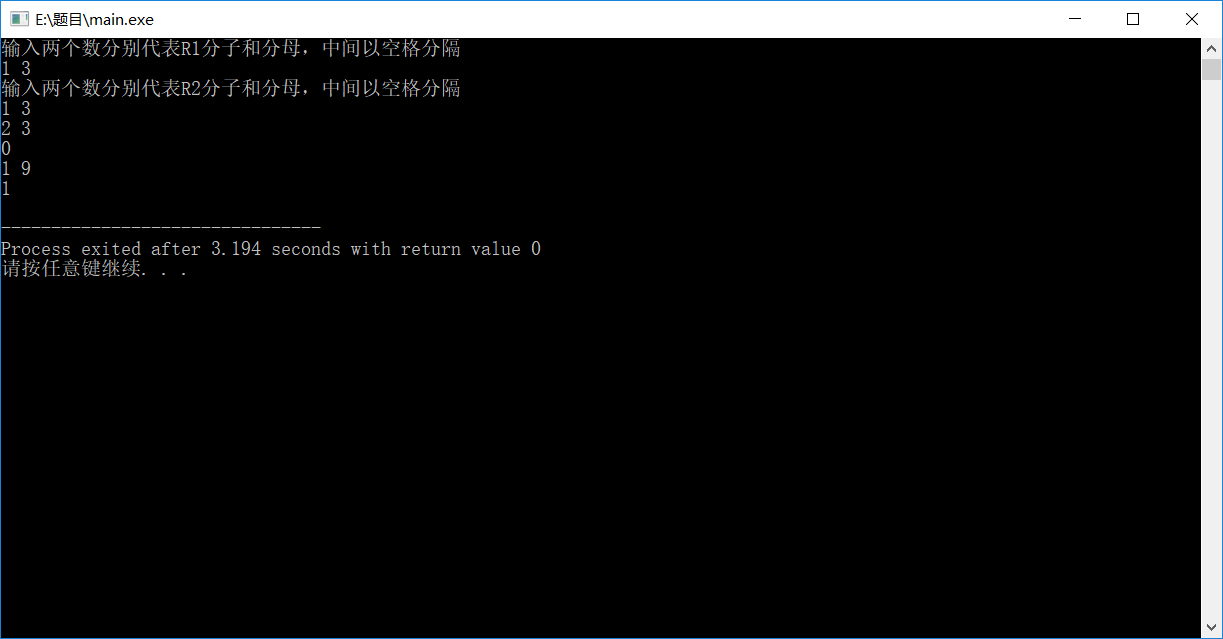
四运行结果

取了两次比较特殊的值

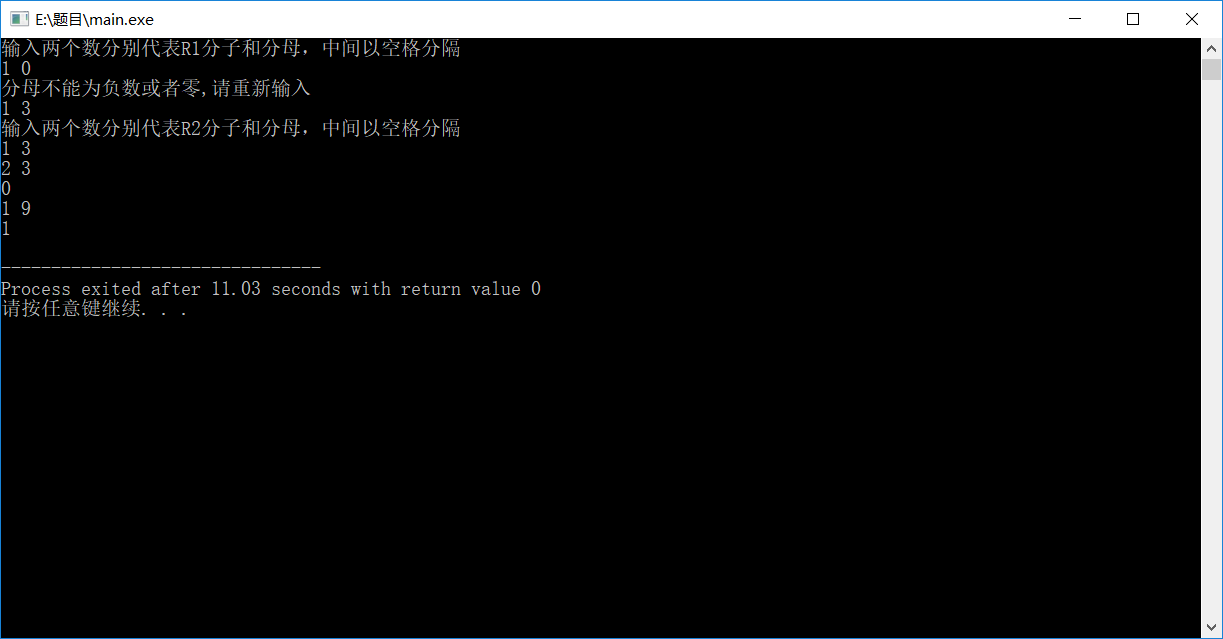
当分母为零时

五总结

　　1.在分数中要注意分子和分母的约分问题

　　2.整数问题也要考虑，结果是否存在负数，抑或是分子分母同时为负时的情况

　　3.在分析代码时要明白作者意图而不是单独对一些细节进行模仿

　　4.既然要申请空间，就不要再申请空间前让系统为其自动分布空间，以防多次申请

posted @ 2018-03-07 00:41 Lumiaa 阅读(175) 评论(1) 编辑收藏举报

刷新页面返回顶部

刘格铭

01——绪论作业

一.作业题目

二.实验要求

三.作业内容

五总结

公告

刘格铭

01——绪论作业

一.作业题目

二.实验要求

三.作业内容

五 总结

公告

五总结