题目补完计划
小 Y 的背包计数问题
题目：
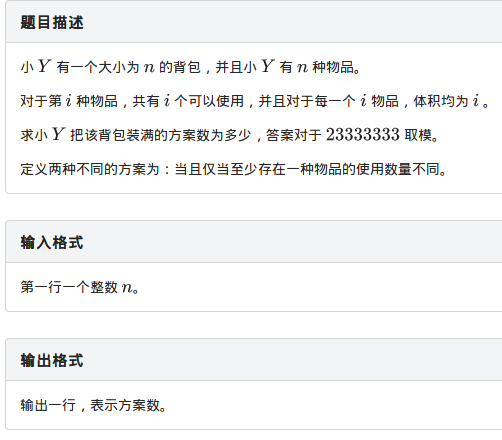
非常小清新的题目描述，就是一个很简单的背包，直接\(n^2\)搞起。
等会，数据范围\(1e5????\)
这咋搞啊？
神犇：\(n\sqrt n\)搞。
以上是我看到这题时候的心里过程，可以无视掉
这道题是一个很厉害的dp和卡常技巧相结合的题，虽说这道题最优复杂度是\(n\sqrt n\)但是只要写丑，实际复杂度会到\(3e7\)以上，加上那么多取膜和\(CCF\)的老爷机，直接\(T\)飞。
先说思路：
定义两个\(dp\)数组，不妨设他们为\(dp\)与\(f\)吧。
\(dp[i][j]\)表示只考虑前\(\sqrt n\)个数，前\(i\)个数，每个数选某些个，占据背包体积为\(j\)的方案数。
\(f[i][j]\)表示\(\sqrt n +1\)~\(n\)这些数中，任意选\(i\)个数，占据背包体积为\(j\)的方案数。
然后我们只要保证得出这两个数组中的值的过程不超过\(n\sqrt n\)的复杂度就行了。
先考虑第一个转移：
比较显然有：\(dp[i][j]=\sum\limits_{k}^{i\times k<=j}dp[i-1][j-k\times i]\)
注意到这样转移的时候需要枚举\(i\)，\(j\)，\(k\)三个变量，复杂度成了\(n^2 \sqrt n\)了，所以需要优化：
考虑前缀和优化：每枚举到一个\(i\)，先\(O(n)\)算出\(sum\)数组，\(sum[j]\)表示\(dp[i-1][j],dp[i-1][j-i],dp[i-1][j-2\times i]……\)的和，然后转移的时候就\(dp[i][j]=sum[j]-sum[j-i\times (i+1)]\)（原因是\(i\)这个物品最多被选\(i\)次，而计算\(sum\)的时候有可能把超过\(i\)件的方案数也统计了过来，所以减一下）。
第二个转移：
运用整数划分的思想，每次加数要么加\(\sqrt n +1\)要么把当前的所有数\(+1\)，就可以拼成所有情况。
\(f[i][j]=f[i][j-i]+f[i-1][j-sqrt(n)-1]\)
因为每个数都是大于\(\sqrt n\)的，所以最多选\(\sqrt n\)个数，\(i\)的枚举边界是这个。
注意这里的j枚举需要从\((\sqrt n +1)*i\)开始枚举，算一个小小的剪枝，但是能把时间从\(1.2s\)剪到\(0.9s\)。
然后综合统计一下，注意判断边界（比如前\(\sqrt n\)个数拼出\(n\)后面那些数拼出0的情况）。
还有记得码写的好看一点。
码：
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
const int mod=23333333;
int dp[320][maxn],sum[maxn],f[320][maxn];
int n;
int main(){
scanf("%d",&n);
register int sqn=sqrt(n);
dp[0][0]=1;
for(register int i=1;i<=sqn;i++){
for(register int j=0;j<=n;j++){
sum[j]=(sum[j-i]+dp[i-1][j])%mod;
}
for(register int j=0;j<=n;j++){
dp[i][j]=sum[j];
if(j>=i*(i+1))dp[i][j]=(1ll*dp[i][j]-sum[j-i*(i+1)]+mod)%mod;
}
}
f[0][0]=1;
int ans=dp[sqn][n];
for(register int i=1;i<=sqn;i++){
for(register int j=(sqn+1)*i;j<=n;j++){
f[i][j]=(1ll*f[i-1][j-sqn-1]+f[i][j-i])%mod;
ans=(1ll*ans+1ll*f[i][j]*dp[sqn][n-j])%mod;
}
}
printf("%d\n",ans);
return 0;
}
