概率与期望题库题目整理
骰子基础版

高中数学题,我是暴力做的。
最多甩24次骰子,可以发现 \(6^{24}\) 没有爆\(unsigned\ long\ long\),直接快速幂搞定分母(基本事件总数)
然后考虑>X点的方案,我是稍微转移下,定义dp[i][j]表示前i个骰子总点数是j的方案数,直接转移搞搞即可,分子也搞定了。
求个gcd约个分,就ok了
三角形的概率

高中数学题,结论题。
答案是:
puts("0.500")
证明看这里神犇LZZ的博客
聪聪和可可

新加的题,是个期望dp,转移和预处理比较复杂,但是不难理解。
定义dp[i][j]表示猫在i,鼠在j的期望时间,运用dfs记忆化搜索的形式dp。
预处理一堆:
- next[i][j]表示猫在i,鼠在j的猫下一步会走哪(根据题目定义,猫会向离鼠近的编号最小的走,可以预处理)
- dis[i][j]表示i到j的距离,每个点bfs一遍\(n^2\)求出
转移(记得期望dp要倒着推):
\(dp[i][j]=dp[next[next[i][j]][j]][j]*\frac{1}{degree[j]+1}+\sum\limits_{k}^{k是j的临接点} dp[next[next[i][j]][j]][k]*\frac{1}{degree[j]+1}\)
这里next两次是因为猫一次走两步,degree[j]+1是因为从j除了到他的临接点,还可以不动,所以老鼠这一步走的总方案数是degree[j]+1。
dp数组的初始化:对于距离为1、2的两点i,j猫吃鼠时间需要1,距离为0的猫吃鼠时间需要0;
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+10;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}#include<bits/stdc++.h>
using namespace std;
const int maxn=2e3+10;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x;
}
int next[maxn][maxn],dis[maxn][maxn],degree[maxn];
int n,m,cat,mouse;
double dp[maxn][maxn];
struct E{
int to,next;
}edge[maxn];
int head[maxn],tot;
void add(int from,int to){
edge[++tot].to=to;
edge[tot].next=head[from];
head[from]=tot;
}
queue<int> q;
void bfs(int s){
for(register int i=head[s];i;i=edge[i].next){
int v=edge[i].to;
dp[s][v]=1;
for(register int j=head[v];j;j=edge[j].next){
int w=edge[j].to;
if(w==s)continue;
dp[s][w]=1;
}
}
q.push(s);dis[s][s]=0;dp[s][s]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(register int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(dis[s][v]>dis[s][u]+1){
dis[s][v]=dis[s][u]+1;
q.push(v);
}
}
}
}
void init(int from,int to){
int Min=0x7fffffff;
for(register int i=head[from];i;i=edge[i].next){
int v=edge[i].to;
if(dis[v][to]==Min){
if(v<next[from][to]){
next[from][to]=v;
}
}
if(dis[v][to]<Min){
next[from][to]=v;
Min=dis[v][to];
}
}
}
double dfs(int u,int v){
if(dp[u][v]!=0||u==v){
return dp[u][v];
}
int now=next[next[u][v]][v];
dp[u][v]+=(dfs(now,v)+1)/(degree[v]+1);
for(register int i=head[v];i;i=edge[i].next){
dp[u][v]+=(dfs(now,edge[i].to)+1)/(degree[v]+1);
}
return dp[u][v];
}
int main(){
freopen("cchkk.in","r",stdin);
freopen("cchkk.out","w",stdout);
n=read();m=read();cat=read();mouse=read();
for(register int i=1;i<=m;i++){
int from=read(),to=read();
add(from,to);add(to,from);
degree[from]++;
degree[to]++;
}
memset(dis,0x3f,sizeof(dis));
memset(next,0x3f,sizeof(next));
for(register int i=1;i<=n;i++){
bfs(i);
}
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
init(i,j);
}
}
printf("%.3lf\n",dfs(cat,mouse));
return 0;
}
return x;
}
int next[maxn][maxn],dis[maxn][maxn],degree[maxn];
int n,m,cat,mouse;
double dp[maxn][maxn];
struct E{
int to,next;
}edge[maxn];
int head[maxn],tot;
void add(int from,int to){
edge[++tot].to=to;
edge[tot].next=head[from];
head[from]=tot;
}
queue<int> q;
void bfs(int s){
for(register int i=head[s];i;i=edge[i].next){
int v=edge[i].to;
dp[s][v]=1;
for(register int j=head[v];j;j=edge[j].next){
int w=edge[j].to;
if(w==s)continue;
dp[s][w]=1;
}
}
q.push(s);dis[s][s]=0;dp[s][s]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(register int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(dis[s][v]>dis[s][u]+1){
dis[s][v]=dis[s][u]+1;
q.push(v);
}
}
}
}
void init(int from,int to){
int Min=0x7fffffff;
for(register int i=head[from];i;i=edge[i].next){
int v=edge[i].to;
if(dis[v][to]==Min){
if(v<next[from][to]){
next[from][to]=v;
}
}
if(dis[v][to]<Min){
next[from][to]=v;
Min=dis[v][to];
}
}
}
double dfs(int u,int v){
if(dp[u][v]!=0||u==v){
return dp[u][v];
}
int now=next[next[u][v]][v];
dp[u][v]+=(dfs(now,v)+1)/(degree[v]+1);
for(register int i=head[v];i;i=edge[i].next){
dp[u][v]+=(dfs(now,edge[i].to)+1)/(degree[v]+1);
}
return dp[u][v];
}
int main(){
freopen("cchkk.in","r",stdin);
freopen("cchkk.out","w",stdout);
n=read();m=read();cat=read();mouse=read();
for(register int i=1;i<=m;i++){
int from=read(),to=read();
add(from,to);add(to,from);
degree[from]++;
degree[to]++;
}
memset(dis,0x3f,sizeof(dis));
memset(next,0x3f,sizeof(next));
for(register int i=1;i<=n;i++){
bfs(i);
}
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
init(i,j);
}
}
printf("%.3lf\n",dfs(cat,mouse));
return 0;
}
OSU!

一道期望dp题,有思考点。
期望是线性的,上数学课的时候,老师这么跟我们说,我们真正理解这句话了吗,我就没有
公式:\(E(kx+b)=k*E[x]+b\)
我们还知道:期望的平方不等于平方的期望
公式:\(E(x^2)\neq E^2(x)\)
但是:\(E^2(x+1)=E^2(x)+2*E(x)+1\)
别问我证明,但他确实是对的
这道题让求后缀1长度3次方的期望和(不是异或3啊)
转化成立方和公式,然后就好求了。
注意我们的E(x)要定义为“后缀1长度为x的期望”,而不是“后缀1长度为x的期望和”,那个不好转移。
转移方程就是:
\(E(i)=(E(i-1)+1)*p[i]\)
\(E2(i)=(E2[i-1]+2*E[i-1]+1)*p[i]\)
\(dp[i]=(dp[i-1]+3*E2[i-1]+3*E[i-1]+1)*p[i]+(1-p[i])*dp[i-1]\)
这个三次方的概率跟之前的不一样是因为它表示的是前i的期望和,是题目中所求。
比较简单就不放代码了。
守卫者的挑战
语文阅读理解题
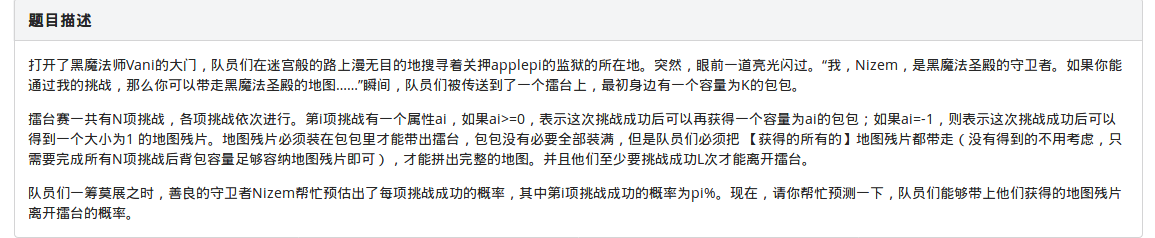
本题的题意较难理解,是本题的难点。
一句话题意:有n项挑战,问通过大于等于L项挑战而且所得背包容量大小大于地图数量的概率
转移类似背包,dp[i][j][k]表示第i轮,已经赢了k轮当前背包剩余容量为j的概率(这里j是可以为负的),直接转移,没啥好说的。
记得,第二维可能是负数,需要加一个值保证为正,类似之前考得某个大模拟。
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e2+1;
double dp[maxn][2*maxn][maxn],p[maxn];
int mode[maxn];
int main(){
int n,l,k;
scanf("%d%d%d",&n,&l,&k);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
p[i]=1.0*x/100;
}
for(int i=1;i<=n;i++){
scanf("%d",&mode[i]);
}
dp[0][k+200][0]=1;
for(int i=1;i<=n;i++){
for(int j=-200;j<=200;j++){
for(int k=0;k<=i;k++){
if(mode[i]>=0){
if(j-mode[i]>=-200)dp[i][j+200][k]+=p[i]*dp[i-1][j+200-mode[i]][k-1];
}else{
if(j+200)dp[i][j+200][k]+=p[i]*dp[i-1][j+200+1][k-1];
}
dp[i][j+200][k]+=(1-p[i])*dp[i-1][j+200][k];
}
}
}
double ans=0;
for(int j=0;j<=200;j++){
for(int k=l;k<=n;k++){
ans+=dp[n][j+200][k];
}
}
printf("%lf",ans);
return 0;
}
Easy

和OSU!是兄弟题,在转移的时候注意下:如果是'o'的话,相当于一个概率为100%的块,'x'的话,相当于一个概率为0%的块,然后这道题是维护后缀1长度平方,比OSU!还简单些。
单选错位

有点i思维但是还是很裸的期望dp。
这道题主要难处理的是每一步的概率,我们可以这样想。
这道题本来有1~a个选项,你答的是1~b中的答案,那答对的概率就是\(\frac{min(a,b)}{a*b}\),通过公式\(P(A)= \frac{事件A发生的情况}{基本事件总数}\)得出
然后就是裸的dp了,这道题并没有严格的要求从前往后推还是从后往前推,正推即可。
太裸了不放代码了
卡牌游戏

写完这道题感觉对约瑟夫问题的递推公式有了更深的理解。
这道题其实是一个概率+约瑟夫问题,在一般约瑟夫中,我们每轮隔着几个人干掉一个人是确定的,这道题确实有概率的。
沿用约瑟夫问题的想法,倒着推。
定义dp[i][j]还剩i个人,1做庄,第j个人的胜率
只有一个人的时候,dp[1][1]=1;他胜利的概率是100%。
然后转移到下一个,枚举上一个转移过来的牌是啥,推出当前这个j是下一轮的哪个人,再由它的概率乘上这张牌的概率,累加到j的答案里面。
大概是这样的:
#include<bits/stdc++.h>
using namespace std;
double dp[61][61];
int a[60],n,m;
int getd(int i,int k){
k%=i;
return 1+k;
}
int main(){
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++)scanf("%d",&a[i]);
dp[1][1]=1.0;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
for(int k=1;k<=m;k++){
int d=a[k]%i;
if(d==0)d=i;
//这里的d就是当前的数字a[k]在i那轮是选中了谁干掉,他的下一号重新标记为1号,多手%一下,可以自己推出来剩i个人,从1开始顺时针第a[k]个是谁。
//然后就能推出来j的上一轮,a[k]步之前,它的编号是啥,然后就可以转移了
//约瑟夫问题的每轮重新编号的思想这里需要运用的很纯熟。
if(d>j)dp[i][j]+=dp[i-1][i-(d-j)]/m;
if(d<j)dp[i][j]+=dp[i-1][j-d]/m;
}
}
}
for(int i=1;i<=n;i++)
printf("%.2lf%% ",dp[n][i]*100);
return 0;
}
换教室

期望开始跟图论结合了,vvv。
这道题并不是太难的图论期望题,还是朴素的期望dp,更像dp一些,状态定义和转移比较难。
先考虑没有概率会怎样。
定义dp[i][j][0/1]第i段课,已经换了j节课,当前这节课换没换。
转移就是:
\(dp[i][j][0]=min(dp[i-1][j][1]+d[i-1]+c[i],dp[i-1][j][0]+c[i-1]+c[i]);\)
\(dp[i][j][1]=min(dp[i-1][j-1][1]+d[i-1]+d[i],dp[i-1][j-1][0]+c[i-1]+d[i]);\)
考虑加入了概率会怎样。
每次换课都有可能成功或不成。
所以我们稍微换一下dp定义:dp[i][j][0/1]第i段课,已经申请换了j节课,当前这节课在哪上的。
每次涉及到换课时候,就直接分概率算,每次申请换课都有可能成或不成。
\(dp[i][j][0]=min(dp[i-1][j][0]+c[i-1]+c[i],dp[i-1][j][1]+p[i-1]*(d[i-1]+c[i])+(1-p[i-1])*(c[i-1]+c[i]));\)
显然如果不换课,通过率是100%,那就没概率啥事,要换课,就有可能不成功,所以这么转移。
dp[i][j][1]的转移类似。
\(dp[i][j][1]=min(dp[i][j][1],min(dp[i-1][j-1][0]+p[i]*dis[c[i-1]][d[i]]+(1-p[i])*dis[c[i-1]][c[i]],dp[i-1][j-1][1]+p[i]*p[i-1]*dis[d[i-1]][d[i]]+(1-p[i-1])*(1-p[i])*dis[c[i-1]][c[i]]+(1-p[i])*p[i-1]*dis[d[i-1]][c[i]]+(1-p[i-1])*p[i]*dis[c[i-1]][d[i]]));\)
就是长了一些,类似一些ex的一堆转移柿子的dp题,但是不难理解
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
return x;
}
const int maxn=4.5e3l+10;
struct E{
int to,val,next;
}edge[5*maxn];
int head[maxn],tot;
void add(int from,int to,int val){
edge[++tot].to=to;
edge[tot].val=val;
edge[tot].next=head[from];
head[from]=tot;
}
double dp[maxn][maxn][2],p[maxn];
int n,m,v,e,c[maxn],d[maxn];
int dis[maxn][maxn],vis[maxn],val[maxn][maxn];
queue<int> q;
void spfa(int s){
dis[s][s]=0;
memset(vis,0,sizeof(vis));q.push(s);
while(!q.empty()){
int u=q.front();q.pop();vis[u]=0;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(dis[s][v]>dis[s][u]+edge[i].val){
dis[s][v]=dis[s][u]+edge[i].val;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
}
int main(){
n=read();m=read();v=read();e=read();
for(int i=1;i<=n;i++)c[i]=read();
for(int i=1;i<=n;i++)d[i]=read();
for(int i=1;i<=n;i++)scanf("%lf",&p[i]);memset(val,0x3f,sizeof(val));
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=e;i++){
int from=read(),to=read(),val=read();
add(from,to,val);add(to,from,val);
dis[from][to]=dis[to][from]=min(val,dis[from][to]);
}
for(int i=1;i<=v;i++){
dis[i][i]=0;
}
for(int i=1;i<=v;i++){
for(int j=1;j<=v;j++){
for(int k=1;k<=v;k++){
dis[j][k]=min(dis[j][k],dis[j][i]+dis[i][k]);
}
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
dp[i][j][0]=dp[i][j][1]=0x3f3f3f3f;
}
}
dp[1][0][0]=dp[1][1][1]=0;
for(int i=2;i<=n;i++){
dp[i][0][0]=dp[i-1][0][0]+dis[c[i-1]][c[i]];
for(int j=1;j<=m;j++){
int pos1=c[i-1],pos2=d[i-1],pos3=c[i],pos4=d[i];
dp[i][j][0]=min(dp[i][j][0],min(dp[i-1][j][0]+dis[pos1][pos3],dp[i-1][j][1]+p[i-1]*dis[pos2][pos3]+(1-p[i-1])*dis[pos1][pos3]));
dp[i][j][1]=min(dp[i][j][1],min(dp[i-1][j-1][0]+p[i]*dis[pos1][pos4]+(1-p[i])*dis[pos1][pos3],dp[i-1][j-1][1]+p[i]*p[i-1]*dis[pos2][pos4]+(1-p[i-1])*(1-p[i])*dis[pos1][pos3]+(1-p[i])*p[i-1]*dis[pos2][pos3]+(1-p[i-1])*p[i]*dis[pos1][pos4]));
}
}
double ans=0x3f3f3f3f;
for(int j=0;j<=m;j++){
ans=min(ans,min(dp[n][j][1],dp[n][j][0]));
}
printf("%.2lf\n",ans);
return 0;
}
奖励关

阅读理解题2
题意又是不很好理解,而且就算理解了思维量也不小。
但是还是逃不出期望dp的范畴,好好想想怎么定义,怎么转移,题目是难不倒我们的!
先翻译题面:
每次有\(\frac{1}{n}\)几率扔出来一个东西,你可以选择捡或不捡(吃还是不吃什么的太奇怪了!)
然后你每捡一个东西,都会加一个值,值可正可负,然后一个物品被捡有前提条件,就是不满足前提条件就不允许捡ta。
问最大的期望。
注意本题n<=15,小的离谱,直接状压搞上,定义dp[i][S]表示第i轮状态为S的期望得分
我们沿用期望dp倒推的思路,考虑每个i,S怎么被转移。
枚举每个被扔出来的物品,它会对这次得分造成一定贡献。
- 如果被扔出来的物品,已经满足它的前提条件,那么我们可以把它塞到现在的答案里,也可能不塞,用类似背包的思路,直接对两种情况取max转移:
\(dp[i][S]+=\sum\limits_{x}^{x\in(1~n)}\frac{1}{n}max(dp[i+1][S],dp[i+1][S|1<<(x-1)]+score[x]);\)
x是枚举的当前蹦出来的那个。 - 如果扔出来的物品,没满足前提条件,那就没法要它的分,直接由dp[i+1][S]转移过来即可。
然后就没了,直接转移就可以得出正确的答案了。最后答案就是dp[1][0]。
码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
double dp[110][maxn];
int pre[maxn],sc[maxn];
int n,k;
int main(){
scanf("%d%d",&k,&n);
for(int i=1;i<=n;i++){
scanf("%d",&sc[i]);
int x;
while(1){
scanf("%d",&x);
if(x==0)break;
else pre[i]|=(1<<x-1);
}
}
int Max=(1<<n)-1;
for(int i=k;i>=1;i--){
for(int S=0;S<=Max;S++){
for(int j=1;j<=n;j++){
int now=1<<j-1;
if((pre[j]&S)==pre[j]){
dp[i][S]+=max(dp[i+1][S],(dp[i+1][S|now]+sc[j]))/n;
}else{
dp[i][S]+=dp[i+1][S]/n;
}
}
}
}
printf("%.6lf\n",dp[1][0]);
return 0;
}
游走
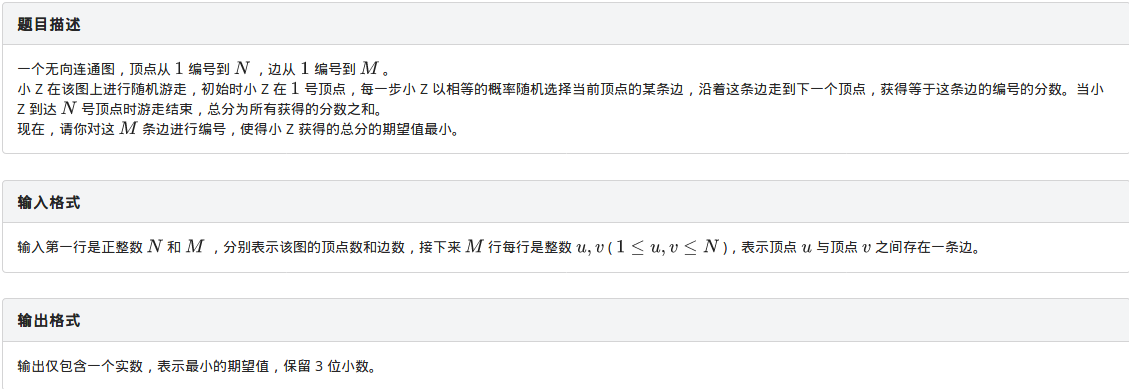
这道题是期望与高斯消元的结合(历史性的会面)之后他俩会经常放在一起ex我们。
这道题主要的思路就是:
求边的期望-->求点的期望-->高斯消元求解-->反推边的期望
几个前备知识:
首先,我们知道边的期望经过次数,等于它端点的期望经过次数×(1/端点的度数)
这挺显然的,一个边只有可能由它的两个端点走过来,那它的期望也一定是两个端点的期望乘上他们经过这条边的概率(如题,就是度数分之一)
接着,我们考虑点的期望怎么求。
一个点只有可能从与它相邻的点转移过来,所以类比上面的结论,一个点的期望,就等于它的邻接点们的期望,乘以它邻接点各自转移过来的概率。
所以,综上我们可以得出一个方程式子:(E表示期望)
\(E(u)= \sum\limits_{v}^{edge(u,v)\in m}\frac{1}{degree[v]}\)
注意:1和n这两个点需要特判,1这个点作为起点,默认已经经过一次,n这个点到这就不会在走,所以他不会去更新它邻接点的答案。也就是说计算一个点的期望时,如果它的邻接点有n,不算1/degree[n]这个值。
接下来,考虑得出这个柿子后,怎么求出每个dp的确定值。
首先:类似dp转移的那种方法肯定不行,每个点都会对别的点有贡献,别的点也会对这个点有贡献,这会出现环,dp转移会转移死循。
所以这道题求出每个点的期望的方法就是解方程辣。
根据上面的柿子,我们发现每个点的期望都最多只会加上n-2个点的期望乘概率,而n的范围允许我们\(n^3\)做,那么就把每个点的转移写成\(a*E[1]+b*E[2]+c*E[3]+d*E[4]+……=x\)的形式,然后发现这是一个矩阵是(n-1)*n的n-1元方程,(不用算n这个点的期望,因为它不会给点贡献期望,所以也不会给边贡献期望),高斯消元即可。
最后统计一下每条边的期望值,从大到小排个序,分别标号1~m然后就出结果了。


