集训DP复习整理
DP复习
集训%你赛2:测绘(审题DP)


经过2000+个小时的努力终于把这道题做出来的蒟蒻通
分析:
这道题我一直没做出来的原因就是因为我太蒟了题面看不懂,题面读懂了,其实不是特别难。
题目翻译:
你从1~n中选k个数,使得误差值小于E。求最少的k。
这里的k都是1~n之间的数字,什么M[]的S[]的先忽略不管他。
现在就是你有n天的数据,你从中选k天,使得这些天的数据与总数据的误差值小于E,找最少的k。
然后通过一些奇怪的方法求出你选的k天的误差值,就ok了。
然后我们开始定义DP数组
dp[i][j]表示前i天中已经选了j天,必须选i这一天的最小误差值。
一个可想到的转移是
dp[i][j]=min(dp[i][j],dp[k][j-1]+calc(k,i));
其中相当于从比i小的数中找一个最优的答案转移过来,clac(k,i)是把最后一个数由k变成i所减少的误差值。
然后我们只要找到一个最小的j使得某个dp[i][j]满足dp[i][j]<=E就可以了。
然后为了处理这个calc,我们可以再引入一些预处理:
我们定义qianzhui[i]表示如果i是所选的天数中最靠前的那个,那么从1到i会产生多少误差值。
houzhui[i]则是如果i是所选天数中最靠后的那个,从i+1到n的误差值。
zhongzhui[i][j]表示如果i到j之间没有选别的天的话(即i,j在所选的天的集合里面是相邻的),从i+1到j-1的误差值。
显然题目描述中已经给出了这三种计算方式。
for(long long i=1;i<=n;i++){
for(long long j=i+1;j<=n;j++){
houzhui[i]+=2*abs(m[j]-m[i]);
}
for(long long j=1;j<=i;j++){
qianzhui[i]+=2*abs(m[j]-m[i]);
}
}
for(long long i=1;i<=n;i++){
for(long long j=i+1;j<=n;j++){
for(long long k=i+1;k<=j-1;k++){
zhongzhui[i][j]+=abs(2*m[k]-m[i]-m[j]);
}
}
}
接下来考虑如何处理这个calc。
显然
把k换成i就只要把k到n的误差删掉,再加上i到n的误差,再加上k到i的误差即可。其他的已选的数不会对这俩造成影响,就没了。
注意只选一个数的时候处理有所不同,可以单独拿出来处理(相当于整了个初始化)
代码:
#include<bits/stdc++.h>
using namespace std;
const long long maxn=110;
long long m[maxn],dp[maxn][maxn];
long long n,E,Min,res_k;
long long houzhui[maxn],qianzhui[maxn],zhongzhui[maxn][maxn];
long long M[maxn],Flag[maxn];
void init(){
for(long long i=1;i<=n;i++){
for(long long j=i+1;j<=n;j++){
houzhui[i]+=2*abs(m[j]-m[i]);
}
for(long long j=1;j<=i;j++){
qianzhui[i]+=2*abs(m[j]-m[i]);
}
}
for(long long i=1;i<=n;i++){
for(long long j=i+1;j<=n;j++){
for(long long k=i+1;k<=j-1;k++){
zhongzhui[i][j]+=abs(2*m[k]-m[i]-m[j]);
}
}
}
memset(dp,0x3f,sizeof(dp));
for(long long i=1;i<=n;i++)
M[i]=0x3f3f3f3f3f3f3f3f+6666666666;
}
long long clac(long long k,long long i){
return houzhui[i]-houzhui[k]+zhongzhui[k][i];
}
int main(){
scanf("%lld%lld",&n,&E);
for(long long i=1;i<=n;i++){
scanf("%lld",&m[i]);
}
init();
for(long long i=1;i<=n;i++){
dp[i][1]=qianzhui[i]+houzhui[i];
if(dp[i][1]<=E){
Flag[1]=1;
}
if(M[1]>dp[i][1]){
M[1]=dp[i][1];
}
}
if(Flag[1]){
printf("%lld %lld\n",1ll,M[1]);
return 0;
}
for(long long i=2;i<=n;i++){
for(long long k=1;k<i;k++){
for(long long j=1;j-1<=k;j++){
dp[i][j]=min(dp[i][j],dp[k][j-1]+clac(k,i));
if(dp[i][j]<=E)Flag[j]=1;
if(M[j]>dp[i][j]){
M[j]=dp[i][j];
}
}
}
}
for(long long i=1;i<=n;i++){
if(Flag[i]){
printf("%lld %lld\n",i,M[i]);
return 0;
}
}
printf("Fail");
return 0;
}
集训%你赛4:免费馅饼(坐标dp)
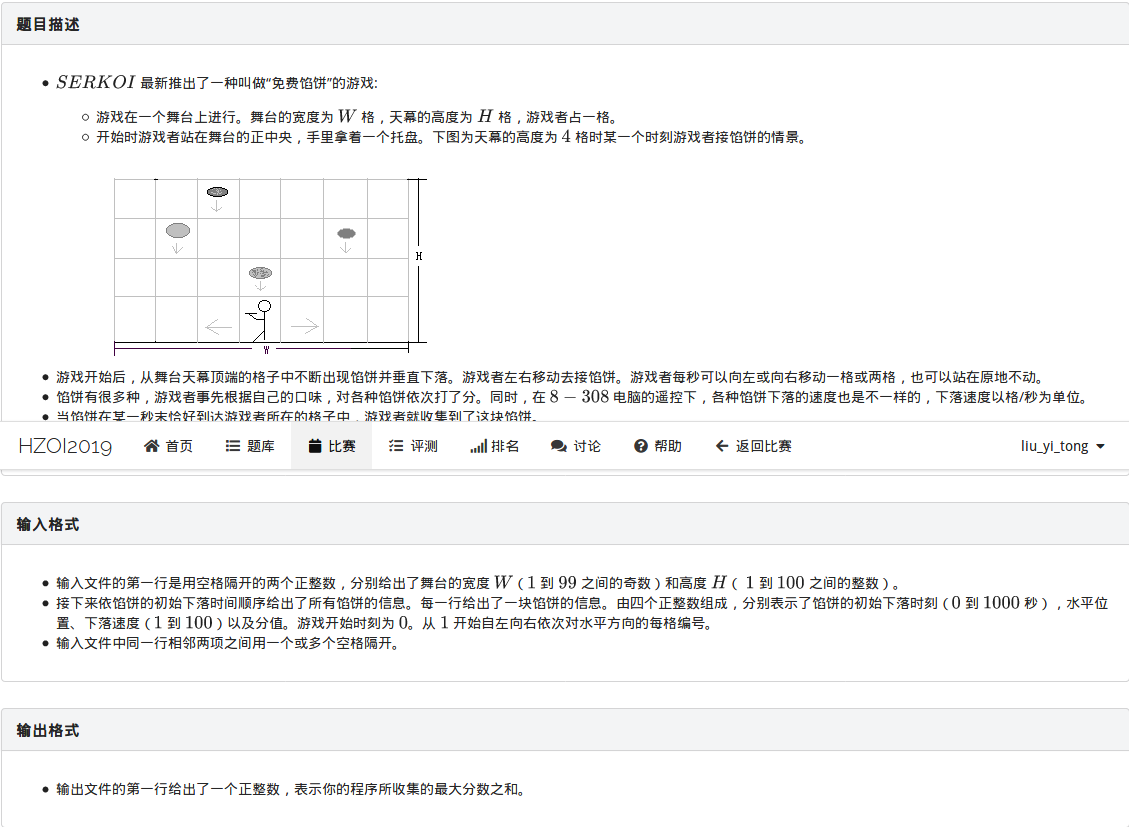
其实思路还蛮好想的,就是定义dp[i][j]表示i时刻在j位置所能收集到的最大值
然后这题有三个注意之处:
- 有些馅饼是不会被收集到的,就是当这个馅饼下落不到高度为1的格子的话,就不会被收集到,那么就不需要考虑这个馅饼,在读入时候就continue掉即可
- 由于我们要处理从舞台中央开始的最大结果,那么我们有两种处理方法:
- 把dp初始值只有dp[0][中央]设为0,其他设置为-INF,这样就不会由于从其他地方开始造成的影响。
- 倒着枚举时间,转移随便,最后只需要输出dp[0][中央]的答案即可。
- 坐标类型的dp需要注意处理细节,主要是关于格子的编号是1还是0为起始行列,从而导致最后枚举的边界减不减1的问题。
代码:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=3000;
typedef long long LL;
int dp[maxn][maxn],val[maxn][maxn];
int W,H,Max_t,Max,start;
int cnt=0;
int main(){
//freopen("a.in","r",stdin);
scanf("%d%d",&W,&H);
int T,D,v,G;
while(scanf("%d%d%d%d",&T,&D,&v,&G)!=EOF){
int t=T+(H-1)/v;
if((H-1)%v)continue;
cnt++;
dp[t][D]+=G;
Max_t=max(Max_t,t);
}
if(cnt==0){
printf("0");
return 0;
}
int add=0;
for(int i=Max_t-1;i>=0;i--){
for(int j=1;j<=W;j++){
add=0;
for(int k=-2;k<=2;k++){
if(j+k>W||j+k<1)continue;
add=max(add,dp[i+1][j+k]);
}
dp[i][j]+=add;
}
}
printf("%d\n",dp[0][(W+1)/2]);
return 0;
}
集训%你赛4:压缩(思维DP)
题目:
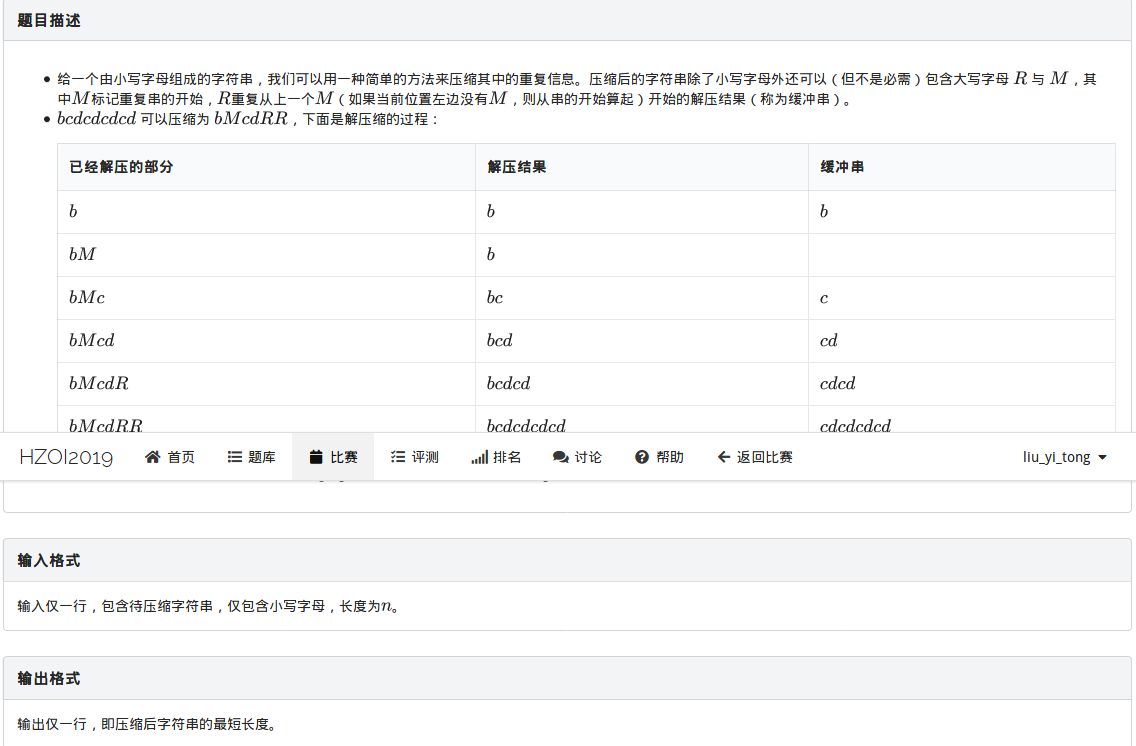
这道题主要是有一些思维的成分在里面,代码实现其实并不复杂。
分析:
这道题其实是一个“区间合并”的过程(跟线段树没关系!!!)
就是每一段区间都可以通过一定的压缩操作变成较短的一段,而无交集的区间之间是不会相互影响的。
然后最后的结果就是把若干个短段通过M操作有机结合起来的过程。
其实就是属于那种别人讲就会,自己怎么推也推不出来的那种
先说定义吧:
dp[i][j]表示i到j这段区间,把i,j当作独立的一段,能通过压缩而形成的最小长度。
为了方便(不这么写就推不出来),我们把i,j这段中含有M的最小压缩长度记为dp[i][j][1],不含M的记为dp[i][j][0]。
转移:
-
一个比较显然的转移是:
if(i到mid与mid+1到j完全一样)dp[i][j][0]=min(dp[i][j][0],dp[i][mid][0]+1);
意思是i到j这段区间压缩后是它的一半加一个R。
因为我们把i到j这一段看作单独的一段,所以默认在队首前自带了M,那么如果出现前半段和后半段完全一样的情况,那么就可以直接压缩成一半的长度。
这里用dp[i][mid][0]而不是(mid-i+1)的原因是i到mid这一段区间也可能压缩,那么我要合并的其实是两段完全一样的压缩过的区间,而不只是两个原区间。
根据题目描述R的特性,手模一下就知道这是对的了。 -
根据上面的例子,我们可以得出下一个:
for(枚举k属于i到j)
dp[i][j][0]=min(dp[i][j][0],dp[i][k][0]+j-k);这主要是考虑有可能i到j这段区间有可能有一个子部分可折叠,即所枚举的i到k这一段,我们这样处理相当于把i到k这段区间的长度加上k+1到j的实际长度,这里没有用到k+1到j的压缩长度是因为k+1在这里不可以看作一个单独的段首,而如果想要压缩k+1到j的话需要加上一个M,而这是在处理i到j区间内部没有M的情况。
-
上面已经囊括了所有dp[i][j][0]的情况了,下面考虑dp[i][j][1]的转移:
for(枚举k属于i到j)
dp[i][j][1]=min(dp[i][j][1],min(dp[i][k][0],dp[i][k][1])+1+min(dp[k+1][j][0]+dp[k+1][j][1]))这个转移方程的意思就是以k为分界线,i到k为一段,k+1到j为一段,中间插入一个M,这样无论是前面还是后面都可以看作一段单独的区间了,那么选它的最小值转移即可,中间的+1是插入一个M的意思。
讨论完转移,就没有啥需要注意的了。
代码:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=3000;
typedef long long LL;
int dp[60][60][2];
char s[60],a[60];
bool check(int i,int j){
if((j-i)%2==0)return 0;
else{
int full=j-i+1;
for(int k=i,kk;(kk=(k+full/2))<=j;k++){
if(a[k]!=a[kk])return 0;
}
return 1;
}
}
int main(){
scanf("%s",s);
int n=strlen(s);
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=n;i++){
a[i]=s[i-1]-'0';
for(int j=i;j<=n;j++){
dp[i][j][0]=dp[i][j][1]=j-i+1;
}
}
for(int len=2;len<=n;len++){
for(int i=1;i+len-1<=n;i++){
int j=len+i-1;
if(check(i,j))dp[i][j][0]=min(dp[i][j][0],dp[i][(i+j)/2][0]+1);
for(int k=i;k<j;k++){
dp[i][j][0]=min(dp[i][j][0],dp[i][k][0]+j-k);
int k1=dp[i][k][0],k2=dp[i][k][1],k3=dp[k+1][j][0],k4=dp[k+1][j][1];
dp[i][j][1]=min(dp[i][j][1],min(k1,k2)+min(k3,k4)+1);
}
}
}
printf("%d",min(dp[1][n][0],dp[1][n][1]));
return 0;
}
集训%你赛5:方格取数(奇怪DP)
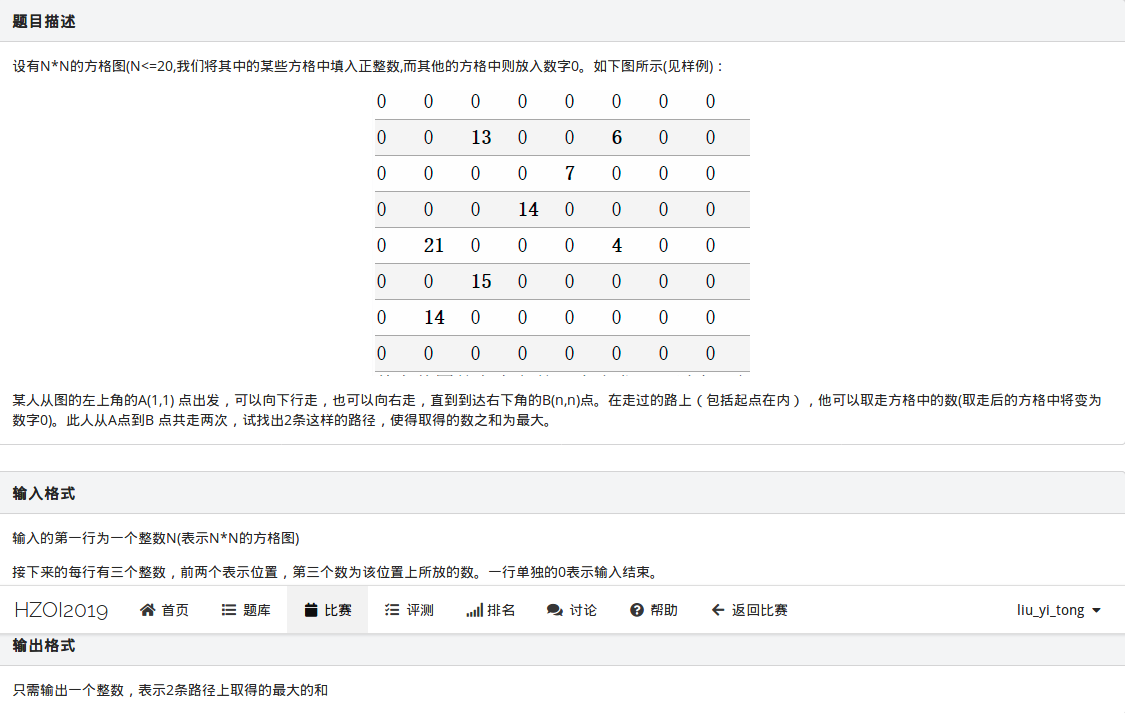
这道题是一个比较另类的dp问题。
我们知道dp的定义一定要满足无后效性,但是这个题你会发现你选过的数会对后面的决策产生影响,有后效性。
所以这道题的重点是考虑如何设计一个没有后效性的dp定义。
我们可以注意,之前的有后效性定义的基础是走到一个点后,这个点在之后不会再被选了。
而一次行走只能向右或向下,所以下一次选这个点一定是在第二次走的过程中,而且走到这里的步数还跟这一次是一样的(因为这个点的坐标i+j一定)
所以我们可以考虑把问题由一个人走两次转化为两个人走一次,让这个一人裂开来,裂成两个人,他们一起走,如果走到一起,那权值只加一个即可。
这样定义的dp[i1][j1][i2][j2]就完全没有后效性了,枚举转移即可。
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=21;
int dp[21][21][21][21],val[21][21];
int main(){
int n;scanf("%d",&n);
while(1){
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
if(x==0&&y==0&&z==0)break;
val[x][y]=z;
}
for(int i1=1;i1<=n;i1++){
for(int j1=1;j1<=n;j1++){
for(int i2=1;i2<=n;i2++){
for(int j2=1;j2<=n;j2++){
if(i1==i2&&j1==j2){
dp[i1][j1][i2][j2]=max(dp[i1][j1-1][i2][j2-1],max(dp[i1-1][j1][i2][j2-1],max(dp[i1-1][j1][i2-1][j2],dp[i1][j1-1][i2-1][j2])))+val[i1][j1];
}else{
dp[i1][j1][i2][j2]=max(dp[i1][j1-1][i2][j2-1],max(dp[i1-1][j1][i2][j2-1],max(dp[i1-1][j1][i2-1][j2],dp[i1][j1-1][i2-1][j2])))+val[i1][j1]+val[i2][j2];
}
}
}
}
}
printf("%d",dp[n][n][n][n]);
return 0;
}
集训%你赛6:小烈送菜(思维DP)
这道题代码巨简单,思维性还是有的。
把一个小烈裂开成两个小烈,一个表示1去到n的过程,另一个表示从1到n剩下的路程,需要回来那一遍走满。
dp[i][j]表示第一个小烈在i,第二个小烈在j的最大值,保证i>j。
我们考虑第i个位置由哪个小烈来走。
转移1:dp[i+1][j]=max(dp[i+1][j],dp[i][j]+w[i]×w[i+1]);(第一个小烈往前走1步)
转移2:dp[i+1][i]=max(dp[i+1][i],dp[i][j]+w[j]×w[i+1]);(i+1位置由靠后的小烈走过来,同时他变成了靠前的小烈)
最后统计结果时候注意枚举第二个小烈最后停的位置,统计最大值。
代码不粘了。
集训%你赛7:搜城探宝(树形dp)
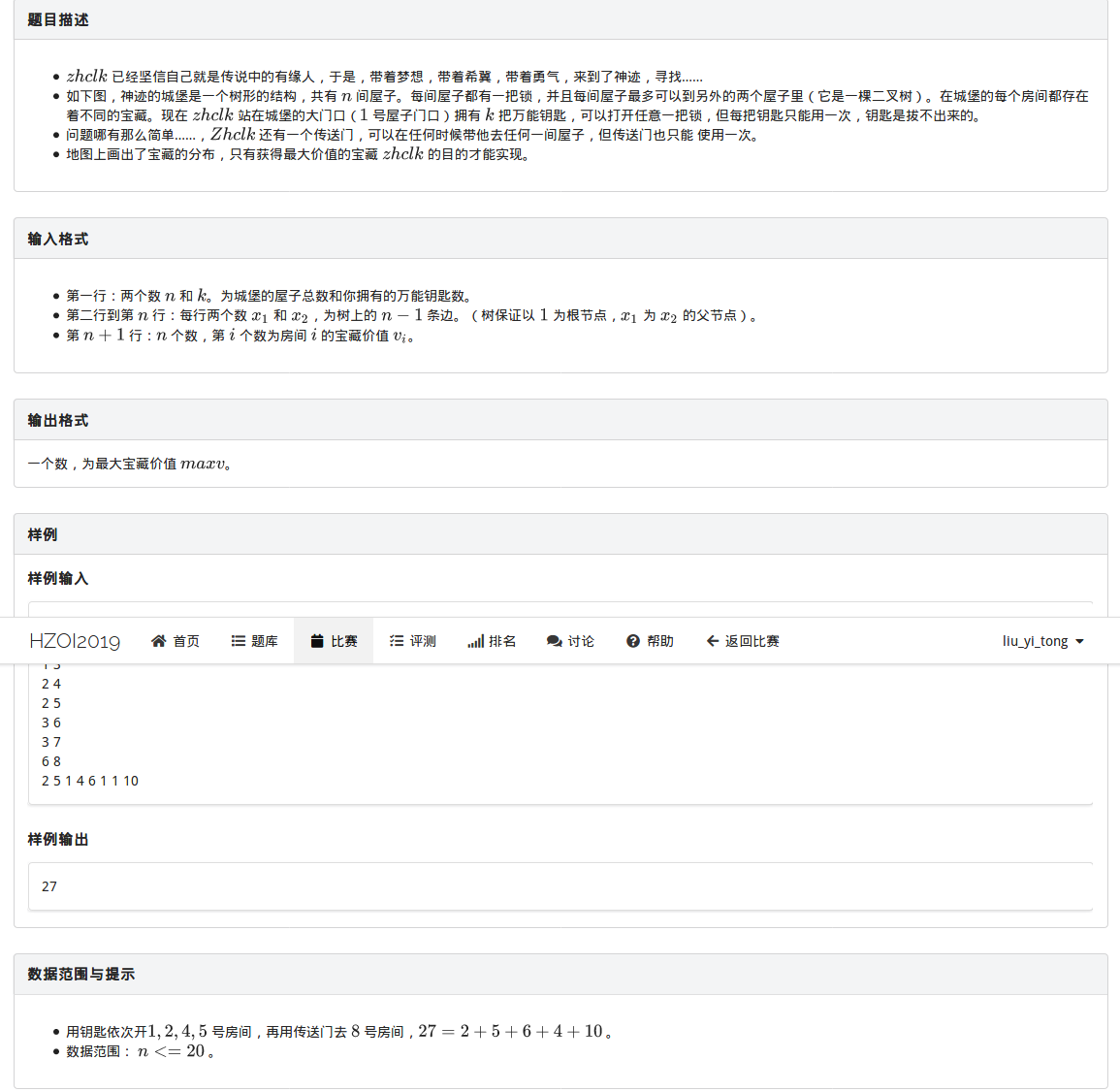
这道题如果没有那个传送门,那就是一个简单的树型dp,复杂度 \(O(2^n)\)
那么加上传送门后怎么处理呢
注意到本题的\(n\)范围是20,这指向\(O(2^n*n)\)
那就是对于每一个点进行\(O(n)\)的操作后再树形dp。
我们不妨枚举每一次被选中由传送门传送过去的点是i,然后把i及其子树从原图中剥离出来,然后挂到一个虚点上,把原图的根也挂到这个虚点上。
那么对这个虚点做树形dp,就是这种情况下的结果。
因为这里有一个性质:
由于一个点是可以随便到达任何他的祖先节点的,因为他一定是由他的所有祖先节点一个一个开锁开过来的,锁开了就可以自由出入了(不这么理解没法解释回溯现象),那么从一个点开启传送门和从这点走回到根节点再开是没有区别的。
这个虚点积累的答案就是从原树上选一段再回到根,再从传送门节点开始选一段再回到传送门的最优解。
由于真正的答案一定是一部分树+传送门和它后面的树,所以这样枚举一定能找到答案
集训%你赛7:MM不哭(思维DP)
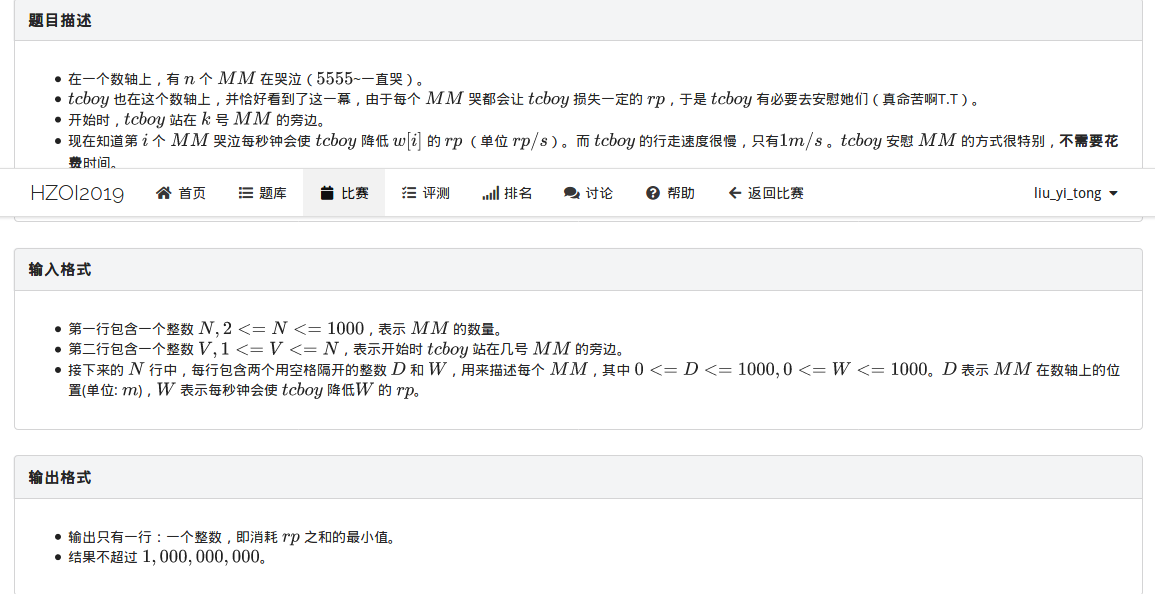
这道题是一个比较经典的区间dp类型,与传染病那道题类似
dp问题比较难处理的部分还是后效性问题。
这道题你如果还是用类似线性dp思想去搞什么安抚前i个人用的时间j之类的,一定会出现后效性。
所以我们这么定义:dp[i][j]表示处理完i,j这段区间所需要的最小时间,由于处理完整个区间一定是停留在区间左或区间右,所以再开一维0/1记录这两种情况。
注意这里的区间是按照人分的,不是按照坐标分的。
下面考虑转移:(0为左,1为右)
dp[i][j][1]=min(dp[i][j][1],dp[i][j-1][1]+calc1,dp[i][j-1][0]+calc2);
calc1是j-1到j的代价,calc2是i到j再到i的代价。
另一种转移类似。
就没辣。
集训%你赛8:子串(思维DP)
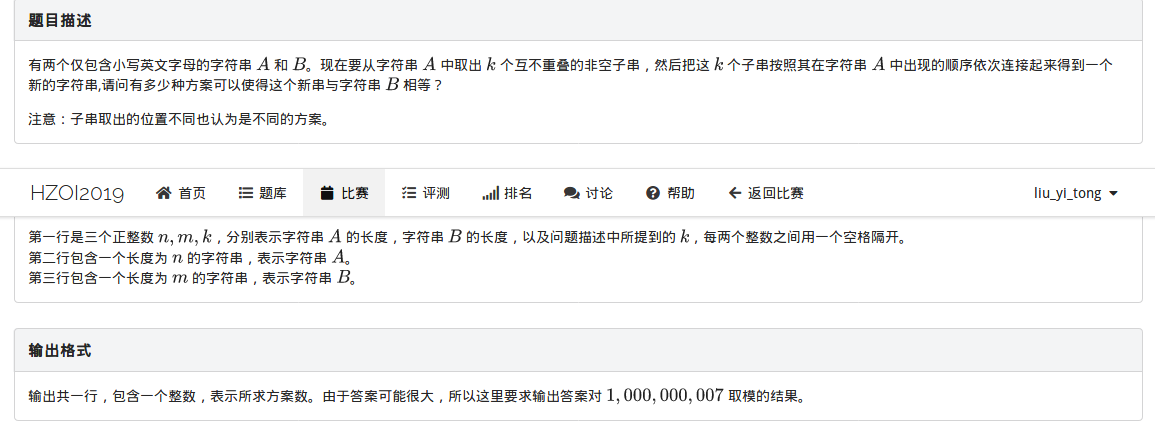
这道题是关于“匹配”的问题,是要用A序列中的一个一个段去匹配B序列,直到把B序列铺满,然后看正好用K段去拼的方案数。
我们可以定义dp[i][j][k][0/1]表示A序列扫到了i,已经选了j段,把B序列匹配到了k,当前这个i选不选入那k段里的方案数。
为什么这么定义呢?
前面3维比较好理解,都是为了求解不得不用到的,因为题目中有“把B序列填满”,“一共选k段”这两个限制条件。
第4维则不太好想。
我们的设计是为了转移服务。
如果没有第四维,我们考虑如何进行转移。
if(a[i]==b[k])dp[i][j][k]=dp[i-1][j][k-1]+dp[i-1][j-1][k-1];如果他两个匹配,那么可以把i,k塞到原来的那第j段里或新开一段。
else dp[i][j][k]=dp[i-1][j][k];不匹配直接放到那j段?
这样对吗?
不对。
问题出在塞到上一个段的时候。
你不知道上一个段最后一个是否匹配了,或者说,一个段的定义就出现了问题。
如果你定义一个段的最后必须是匹配的,那么else里面的就没法转移了,会丢失情况。
如果你定义一个段包括前面一段匹配的,后面一段不匹配的,那么你无法得知当前这个段的末尾是匹配的还是不匹配的。
显然第二种定义方式的问题较小,比较好处理,就是再加一维,表示处理到i时候最后一个是匹配的还是不匹配的,如果匹配,那么相当于这个i放入了第j个段中,反之亦然,那么就可以开始正确的转移了。
if(a[i]==b[k]){
dp[i][j][k][1]+=dp[i-1][j-1][k-1][0]+dp[i-1][j-1][k-1][1];//新开一段
dp[i][j][k][1]+=dp[i-1][j][k-1][1];//塞到原来那段里面
}else{
dp[i][j][k][0]+=dp[i-1][j][k][0]+dp[i-1][j][k][1];
}
然后就没了。
集训%你赛9:步步为零(思维DP)

这道题看上去就是一个很裸的题,其实跟dp的思想都没啥关系。
定义dp[i][j][k]为在i,j这个点,能不能算出来k这个值。
我们把整个图转化成前i行正三角,后i-1行倒三角的形式,然后枚举到当前节点后能到达的值,标记一下,再转移均可。
为什么要转化这个图呢,因为这样转化后每个点就只会从i+1,j+1与i+1,j转移过来,比较好处理。
注意有可能是负值,那么转移的时候多加个2500就可以了。
集训%你赛11:排队(思维DP)
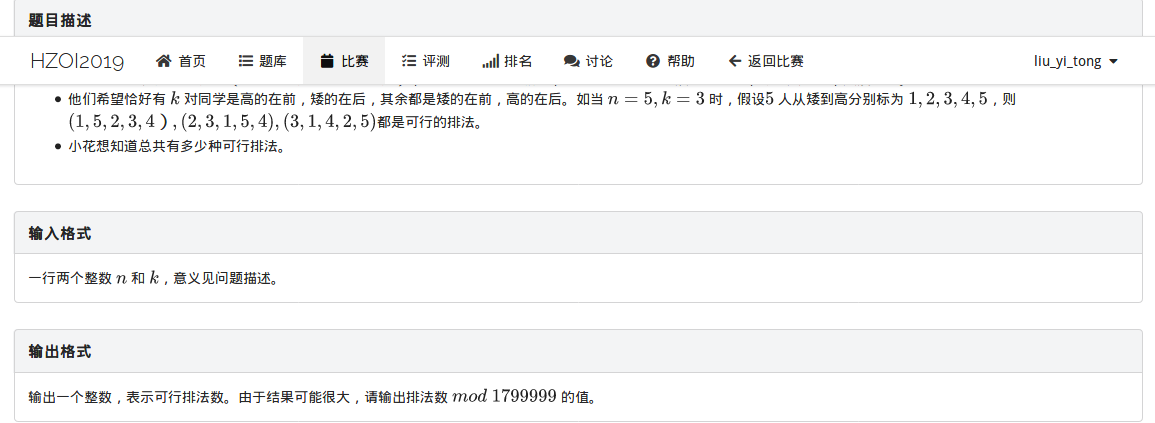
其实是个找规律题
我们定义dp[i][j]表示放了i,出现高-矮对数为j对的方案数。
我们考虑转移
因为这道题人们的高度都是从小到大的,所以我们的dp[i]不是表示前i个人,而是i这个高度,默认从小到大一个个插入,保证最后的结果满足遍历到所有情况即可。
dp[i][j]=dp[i-1][j]+dp[i-1][j-1]+……+dp[i-1][j-i];
这个转移是相当于把i随机插入到之前i-1个数中,由于i大于其中任何一个数,所以插在哪里,它后面的数的数量就是增加的高-矮对数。
最少:插入整个队列最后面,一对也不加。
最多:插入到整个队列最前面,加i-1对。
所以就得到了这个转移。
我们注意到i的范围是100,j的范围是10000,直接这样转移复杂度10010010000是不可以的。
考虑如何优化:
错位相减见老姚博客
2.这个式子一看就很可以前缀和维护,直接砍掉一个100,复杂度O(1e6)可过。
集训%你赛12:小象与老鼠(DP)
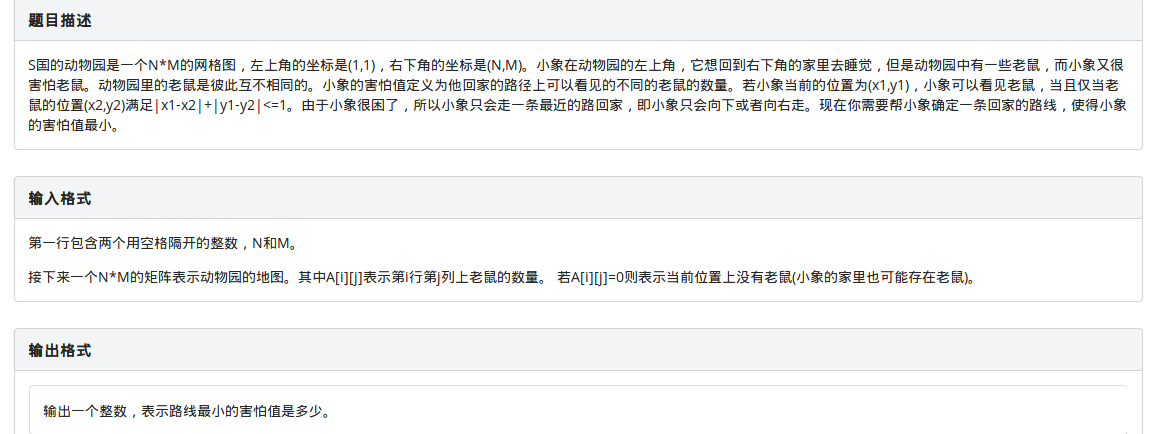
类似一个二维图里面的dp,主要难点还是dp的无后效性。
由于小象所看到过的老鼠只能计算一次,所以导致了当前位置计算过的老鼠的数量可能对后面产生影响。
为处理这个问题,我们给dp数组加上一维dp[i][j][0/1]表示到i,j这个位置的代价,从上面转移下来的记为0,从左面转移下来的记为1。
为什么这样写就能解决问题了呢,因为这道题有一个这样的性质,本次状态产生的代价只可能与转移到这里的状态的上个状态产生的代价重复,而不会跟更远的重复。
例子:
如果一个位置的老鼠被算重了,那么一定只能是经过他左边和下边(小象路线下、右),或者是经过他的上面和右面(小象路线右、下),而这两种情况下小象都是只走了三个结点,而且都是第一个和第三个结点算重了。
那么具体是怎么的转移的呢?
dp[i][j][0]+=dp[i-1][j][0]+a[i+1][j]+a[i][j-1]+a[i][j+1];小象路线下、下,不会有算重的部分,直接加上当前点周围的三个区域的老鼠即可。
dp[i][j][0]+=dp[i-1][j][1]+a[i+1][j]+a[i][j+1];小象路线右、下,那么当前结点左侧的老鼠已经被算过了,那就不加他们了。
dp[i][j][1]的两个转移方程类似,这里就不多赘述了。
集训%你赛13:人品问题(树型DP)
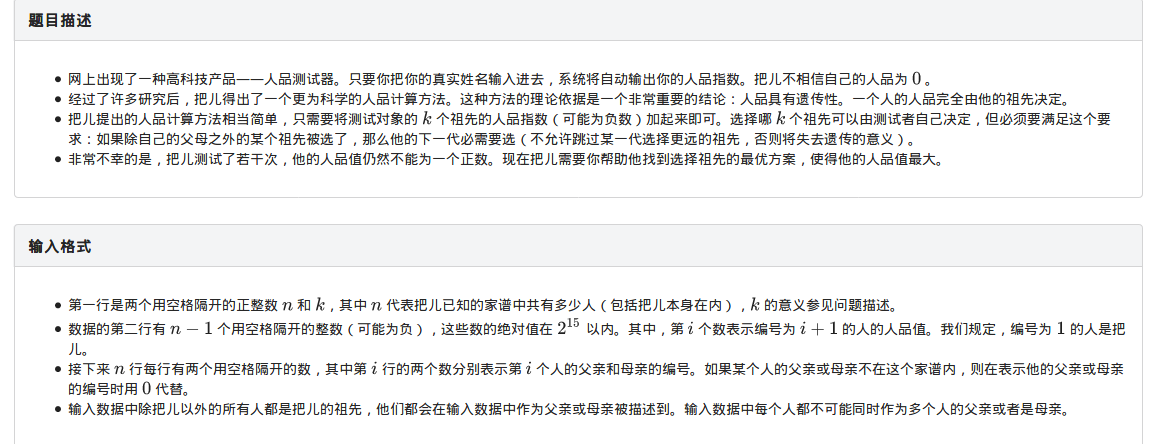
就是以自己这个节点为根,连向他的父母,这样在以自己为根的树上找几个连续的点,使他们的和最大。
就是裸的树形dp。
没啥要注意的,也就是之前那个搜城探宝的弱弱弱化版




