《机器学习》第二次作业——第四章学习记录和心得

思维导图：

第四章 线性判据与回归

一．线性判据基本概念和学习概述

1.生成模型（给定训练样本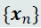，直接在输入空间内学习其概率密度函数）
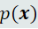优势：可以根据采样新的样本数据；可以检测出较低概率的数据，实现离群点检测。
劣势：高维的x，需要大量训样本才能准确的估计（维度灾难问题）。
2.判别模型（给定训练样本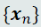，直接在输入空间内学习其概率密度函数）
优势：快速直接，省去了耗时的高维观测似然概率估计。
3.线性判据
（1）定义：

（2）优势：计算量少；适用于训练样本较少的情况。
（3）模型：

（4）判别公式：

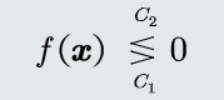
（5）决策边界方程：

（6）任意样本到决策边界的距离：

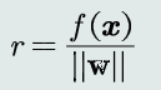
该距离r的绝对值越大，这个值的正类或负类的程度越大；是样本x到决策面H的代数距离度量。
4.目标函数
（1）核心思想：如何实现有效决策
（2）求解：最小化/最大化目标函数（解析求解和迭代求解）
（3）约束条件：加入约束条件，提高泛化能力

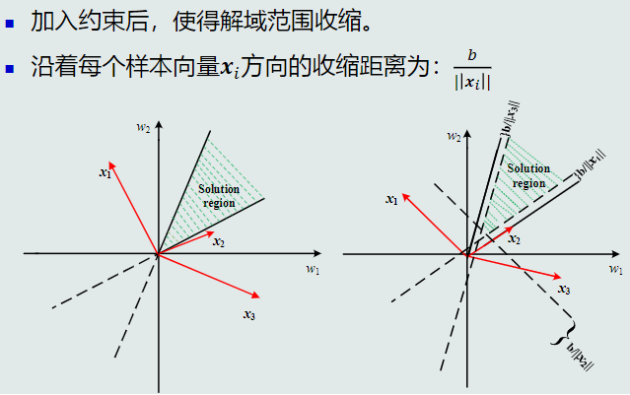
二．并行与串行感知机算法

1.预处理
（1）目的：

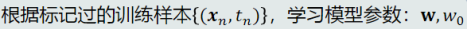
（2）步骤：

2.梯度下降法（当前梯度值迭代更新参数）

3.并行感知机
（1）目标函数：针对所有被错误分类的训练样本，其输出值取反求和：

（2）参数更新：

（3）算法流程：

4.串行感知机
（1）目标函数：针对被错误分类的训练样本，最小化其输出值取反：

（2）算法流程：

三．Fisher线性判据

1.目标函数：

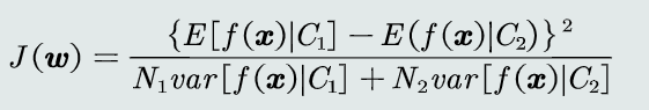
2.决策边界方程：

3.训练算法流程

四．支持向量机

1.基本概念

2.学习算法：构建拉格朗日函数和构建对偶函数
3.优化方法：拉格朗日乘数法和拉格朗日对偶法