线性回归代码实现（matlab）

1 代价函数实现（cost function）

 

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0; 

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.

predictions = X * theta;
sqrErrors = (predictions-y) .^ 2;

J = 1/(2*m) * sum(sqrErrors);



% =========================================================================

end

　　1.1 详细解释

转化成了向量（矩阵）形式，如果用其他的语言，用循环应该可以实现

predictions = X * theta;        % 这里的大X是矩阵

　　

 

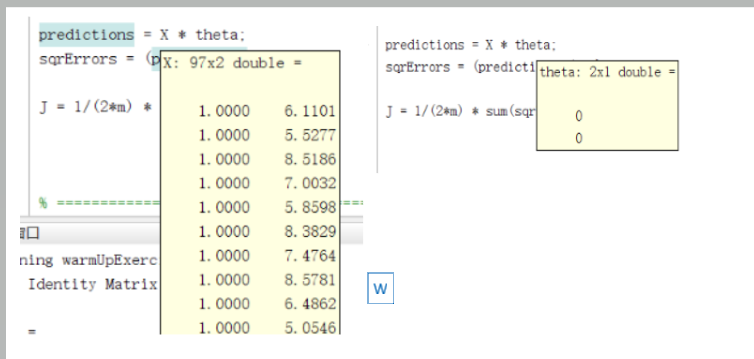
sqrErrors = (predictions-y) .^ 2;

　　

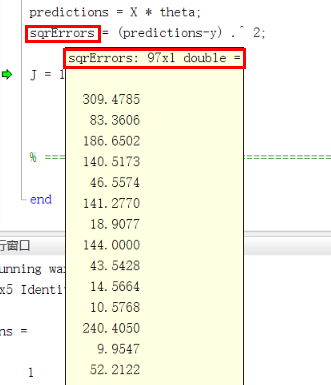
2 梯度下降

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    theta_temp = theta;
    for j = 1:size(X, 2)
        theta_temp(j) = theta(j)-alpha*(1/m)*(X*theta - y)' * X(:, j);
    end
    theta = theta_temp;





    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end

end

　　2.1 解释

J_history = zeros(num_iters, 1);

 

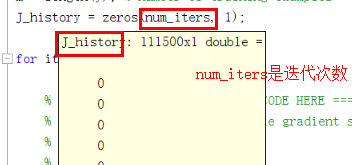
theta_temp = theta;  

　　把theta存起来。保证同时更新

for j = 1:size(X, 2)
        theta_temp(j) = theta(j)-alpha*(1/m)*(X*theta - y)' * X(:, j);
    end

　　更新theta    

(X*theta - y)' 是转置

(X*theta - y)' * X(:, j);

　　这步是求和，相当于sum

 

  J_history(iter) = computeCost(X, y, theta);

记录代价函数

因为随着迭代次数的增加，代价函数收敛。theta也就确定了。

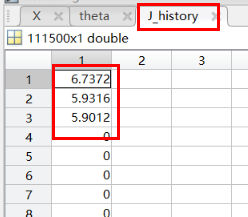
代价函数的是降低，同时theta也在变化

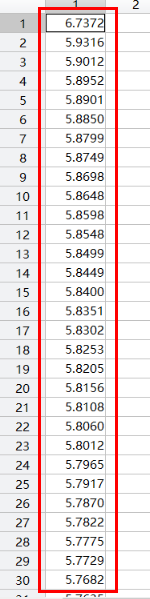
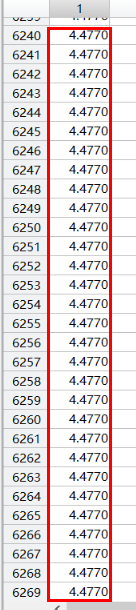
到后面代价函数的值已经不变化了。到收敛了