力扣240(java&python)-搜索二维矩阵 II(中等)
题目:
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
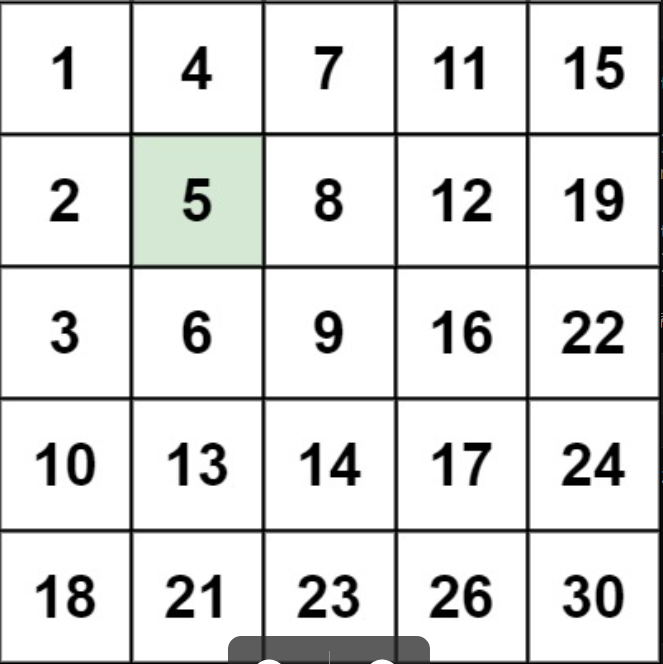
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
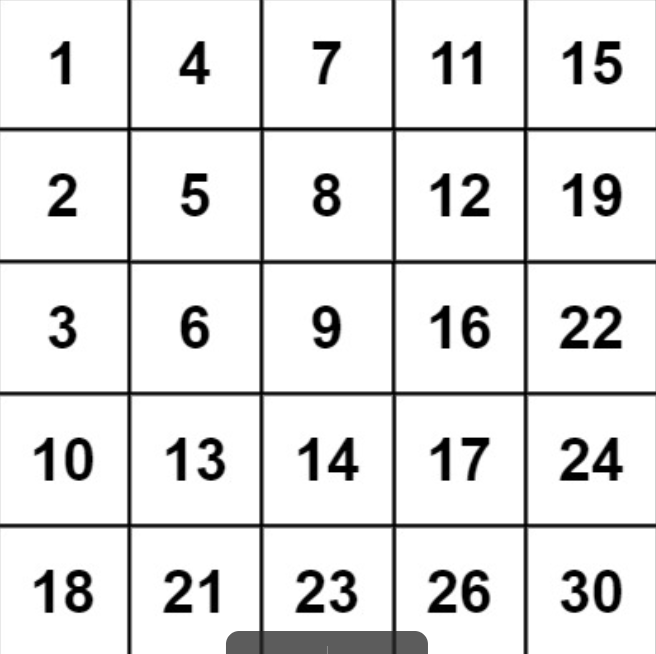
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= n, m <= 300
- -109 <= matrix[i][j] <= 109
- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
- -109 <= target <= 109
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/search-a-2d-matrix-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路:
【二分查找】
这题与 74.搜索二维矩阵 区别在于 不能保证每一行的第一个整数大于上一行的最后一个整数,故可以以行为基准,先遍历一行,再从这一行去遍历每一个数字,从而判断出该行是否存在target,不存在又继续遍历下一行的每个数字。(或者以列为基准,先遍历一列,再从这一列去遍历每个数字,从而判断出该列是否存在target,不存在又继续遍历下一列)行:martrix.length,列:martix[0].length
java代码(left < right)--- 以行为基准:
1 class Solution { 2 public boolean searchMatrix(int[][] matrix, int target) { 3 //n:行;m:列 4 int n = matrix.length, m = matrix[0].length; 5 for (int i = 0; i < n; i++){ 6 int left = 0, right = m-1; 7 while (left < right){ 8 int mid = left + (right - left + 1) / 2; 9 if (target >= matrix[i][mid]){ 10 left = mid; 11 }else{ 12 right = mid - 1; 13 } 14 } 15 if (matrix[i][left] == target) return true; 16 } 17 return false; 18 } 19 }

python3代码(left <= right)--- 以列为基准:
1 class Solution: 2 def searchMatrix(self, matrix: List[List[int]], target: int) -> bool: 3 n, m = len(matrix), len(matrix[0]) 4 # 以列为基准 5 for i in range(m): 6 left , right = 0, n - 1 7 while left <= right: 8 mid = left + (right - left) // 2 9 if target > matrix[mid][i]: 10 left = mid + 1 11 elif target < matrix[mid][i]: 12 right = mid - 1 13 else: 14 return True 15 if target == matrix[right][i]: 16 return True 17 return False






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)