求最大公约数

求最大公约数伪代码

求两个数的最大公约数的欧几里得算法（辗转相除法）

• 欧几里得算法又称辗转相除法，用来求两个正整数的最大公约数。以上面的1997和615为例，用欧几里得算法求解如下：

    1997=615×3+152
    615+152×4+7
    152=7×21+5
    7=5×1+2
    5=2×2+1
    2=1×2+0
  

当被加的数为0时，可以得出，1997和615的最大公约数为1。以上做法的依据是以下定理：两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。

• 程序框图如下：
  
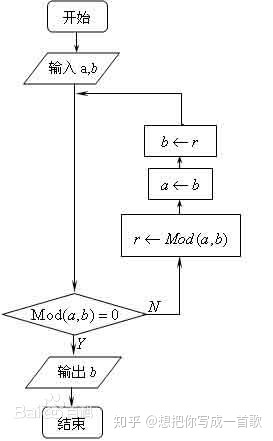
  网上链接如下：https://zhuanlan.zhihu.com/p/51411526

伪代码如下：

input a,b;   //输入两个整数。
create r;    //中间量用来存放余数。
while(b>0)
{
r=a%b;
a=b;
b=r;
}
output a;   //当b=0时，a即为最大公约数。

手动走伪代码并测试

选择a=50,b=36,r=14;
重新赋值后a=36,b=14,r=8;
再次赋值后a=14,b=8,r=6;
再再次赋值后a=8,b=6,r=2;
再再再次赋值后a=6,b=2,r=0;
再再再再次赋值后a=2,b=0。于是输出2,2为50和36的最大公约数。
所以伪代码无误。