机器学习公开课备忘录（二）神经网络与BP算法

机器学习公开课备忘录（二）神经网络与BP算法

神经网络是针对特征过多，分布非线性的监督学习类问题提出的，模仿人类大脑的工作方式。例如：图像判别

前向算法

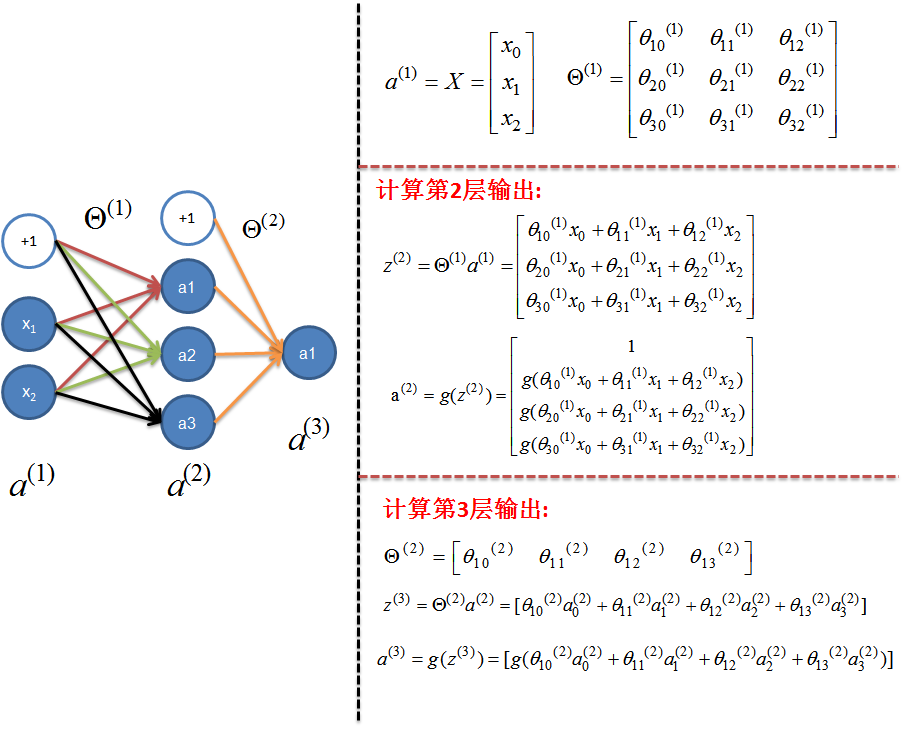
下面这张取自 http://www.cnblogs.com/python27/p/MachineLearningWeek05.html 的图片可以很好地说明前向算法，对于神经网络，特征所在的层称为输入层，即此处的\(a^{(1)}\);结果层被成为输出层，即为此处的\(a^{(3)}\)，中间的层都被成为隐藏层。
可以看到，计算隐藏层及输出层的神经元输出，即是对输入层的输入进行加权，然后做sigmod映射，每一层还会额外增加偏置项，即常数项。

神经网络既可以用于回归问题，也可以用于分类问题。公开课讲述的是以分类问题作为例子的，对于二分类问题，可以根据输出层和阈值来进行划分是\(0 或 1\)；但对于多分类问题，往往\(k\)个分类会在输出层设置成\(k\)个单元，每个输入值的结果写成\(\{1 0 0 0 ...\}\{0 1 0 0 ...\}\{0 0 1 0 ...\}\)的形式，即若输出标记为第\(k\)类，则第\(k\)个元素为1，其余均为零。然后求出无标记数据的输出结果后，对输出层最接近1的神经元置1，其余置0，来得到其类别。

BP算法

BP算法解决的是如何求解层与层之间映射参数的求解问题，即此处的\(\Theta^{(1)}、\Theta^{(2)}\)如何求解的。参数求解的思路和之前线性回归逻辑回归是类似的。
假设现在用神经网络解决一个多分类问题，输出类别有\(k\)个，即最后一层的神经元个数有\(k\)个，对于一个神经网络，定义了其代价函数：

\[J(\Theta) = -\frac{1}{m}\left[\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{K}y^{(i)}_{k}log(h_\theta(x^{(i)}))_k + (1-y^{(i)}_k)log(1-(h_\theta(x^{(i)}))_k)\right] \]

然后通过梯度下降来求解参数，BP算法实质上神经网络对梯度下降法的使用。
定义：\(\delta_j^{(l)}\) 为第 \(l\) 层第 \(j\) 个神经元的误差：

\[\delta^{(3)}=a^{(3)}-y \]

\[\delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g'(z^{(2)}) \]

当 \(l\) 数量更多的时候，对每个隐藏层，都有$$\delta^{{(l)}=(\Theta})^T\delta.*g'(z^{(l)})$$
求出误差后，就可以求出导数项了:

\[\frac{\partial J(\Theta)}{\Theta_l} = \delta^{(l+1)}(a^{(l)})^T \]

视实际运算时神经元输出的列向量或行向量表示，这里的顺序可能有一些差异，但是最后求出导数的维数和 \(\Theta_l\) 的维数必定是相同的。
这里公式的具体推导依赖链式法则，具体可以看上述的博文或者UFLDL。
最后，是梯度下降法的更新过程，对于 \(m\) 个样本：
for i=1:m

• \(a(1)=X\), FP算法计算各层的 \(a^{(l)}\)
• 计算最后一层误差，\(\delta^{(L)}=a^{(L)}-y\)，BP反向传播计算\(\delta^{(L-1)}, \delta^{(L-1)}, \ldots, \delta^{(2)}\)
• 累加 \(\Delta^{(l)}=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T\)

end
然后计算梯度：

\[D_{ij}^{(l)}=\frac{1}{m}\Delta^{(l)}_{ij},   j=0 \]

\[D_{ij}^{(l)}=\frac{1}{m}\Delta^{(l)}_{ij}+\lambda\Theta_{ij}^{(l)},  j\neq 0 \]

\[\frac{\partial J(\Theta)}{\partial \Theta^{(l)}}=D^{(l)} \]

上述的第二个公式计入了正则项，但是偏置单元不用考虑正则项，因此造成了两种不同的情况。

神经网络算法的使用

1. 确定神经网络结构
2. 执行训练过程
   a.随机初始化权重（统一初始化为零会导致权重始终相同的问题）
   b.执行FP算法与BP算法，遍历所有样例，累计所有的 \(\Theta\)
   c.加入正则项，计算出导数
3. 梯度检验，利用 \(\frac{\partial J(\Theta)}{\Theta} \approx \frac{J(\Theta+\varepsilon) - J(\Theta-\varepsilon)}{2\varepsilon}\) 的公式确保算法正确性
4. 去掉梯度检验，以防止浪费大量时间，然后开始迭代，求出 \(J(\Theta)\) 最小时的 \(\Theta\) 参数