树的点分治
START
[参考资料:漆子超《分治算法在树的路径问题中的应用》+李煜东《算法竞赛进阶指南》]
本片总结讨论点分治。
- 分治,指的是分而治之。即将一个问题分割成一些规模较小的相互独立的子问题,以便各个击破
- 点分治:首先选取一个点作为根结点使无根树变成有根树,再对每棵子树进行递归求解。为了缩小问题规模,这个点应为重心,即以它为根,最大子树的规模能够尽可能小的节点(可以证明,以重心为根时,最大子树的节点数不超过N/2)
- 这个算法可能的来由:假设我们要做树上的路径问题。朴素做法是从每个点出发,遍历它的所有子孙节点。但这样的时间复杂度是N^2的。为什么慢?以极限数据——一条链举例,每次都DFS,那么访问的子孙个数:N,N-1,N-2……1。也就是说,这样做,使的访问的子树规模不能快速地缩小,导致了许多节点被重复访问,于是T了。怎么解决呢?就从这里入手,我们想要使得子树规模小,那就要它们尽可能平均分配,使得每进入一层,“淘汰”掉的节点数尽可能多,效率就能高很多。这正是点分治的奇妙所在。
- 一点感想:第一次在寒假时看,明显理解得不透彻,代码也是半抄半写。暑假时重温,自己通过原理捋顺了思路,瞬间柳暗花明。所以,在发现不懂时,要从原理出发,自己想一遍,硬啃、硬背别人的代码没有任何用处!!!
- 在写例题1时,还是发现了很多问题,从一大堆注释+调试信息中就可以发现我的码力是有多么菜了。路越遥,码力越要提升。加油~
【例题1:Tree poj1741】
题目大意:
给定一棵N个节点、边上带权的树,再给出一个K,询问有多少个数对(i,j)满足i<j,且i与j两点在树上的距离小于等于K。
多组测试数据,每组数据满足N≤10000,1≤边上权值≤1000,1≤K≤10^9。
分析:
假如给你一个棵树,形如:
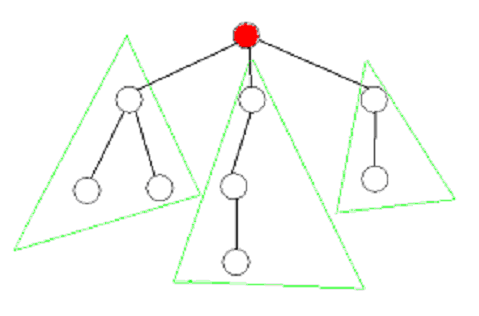
目前运行到红点,不难分析出,路径存在以下两种:
1) 路径不经过根结点
2) 路径经过根结点
感觉上这两种需要单独处理,其实不然。1)虽然不经过目前的根结点,但是可能经过子树,子子树的根结点……也就是说,其实道理是一样的,那么解决1),只需通过递归,进行与2)的操作即可。
那么,如何求解2)呢?
根据题目对路径的要求,合法点对(i,j)必须满足i到根的距离+j到根的距离小于等于k并且i,j不属于同一棵子树中。
于是,定义dis[x]表示节点x到目前的根节点的距离。belong[x]表示节点x所属的子树。
如果直接考虑得到目标解,显然不易求。换个“大减小”的思路。
目标解=
dis[i]+dis[j]<=k的点对数 -
dis[i]+dis[j]<=k并且i,j属于同一棵子树中的点对数。
先考虑前者怎么求。自然不能用N^2大暴力。但是有序的话就好做很多了。因此,可以对根结点的所有子孙节点到它的距离排序,然后利用单调性,不难YY出一个O(N)的做法(双指针扫描/尺取法)。
至于后者呢?需要另外想做法吗?其实不用的。仍是化异为同思想。实际上就是在特定的子树中进行类似操作。不过值得注意的是,需要初始化该子节点的dis值为该边的权值,问题就能够成功转化。
但是,如果只是任选一个点作为根进行上述操作,很显然会TLE。因为当树是一条链时,复杂度是N^2的。
因此,为了使得子树规模快速缩小,每次处理一棵树时,就要先找出它的重心作为它的根。然后才能进行一系列的操作。
至于重心的求法,其实并不难。加入我们在一棵树中找重心,该树总的大小为all。假定我们选定x为根,那么当它为根时,各子树大小就为, x的各儿子的子树大小 以及all-x的子树大小。要做到这些,只要在求重心前,对该树进行一次dfs,预处理出各子树大小即可。
整理一下该题算法流程:
- 找重心
- 计算各子孙与重心的距离
- 计算所有点对
- 逐个访问儿子,先减去不合法点对,再递归求解儿子
时间复杂度怎么求?根据找重心的方法,以及每棵子树大小不超过整棵树大小的一半这条定理,因此最多共logN层。每层会对dis进行汇总+排序,故总的时间复杂度为O(N*logN*logN)
另外,由于这里涉及多个函数,使用全局变量更能使代码简洁美观。但是注意,递归中一定要对全局变量进行回溯的处理,否则就会对答案造成重大影响,甚至是RE!!!
还有,有时候因为懒,会在输入时定义局部变量。但是,并非所有的变量都可以这样。例如本题,如果输入时定义局部变量k,就会导致递归函数中访问到的k=0,造成严重的错误。
最后,对于deep[i]写成dis[i],能够说明两点,一是不要使用意思太相近的数组名,容易搞混;再者写之前想好其表示的意义!
这一轮调试,太酸爽了。
本题编码中给我的最大警醒,就是对变量要求的仔细思考!!!!!
代码如下:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<vector> 5 #include<cstring> 6 using namespace std; 7 const int MAXN=1e4+5; 8 int dis[MAXN],f[MAXN],v[MAXN],deep[MAXN]; 9 int stand,last,k,inf=0x7fffffff,ans,newroot,n; 10 //n,k定义全局变量!!! 11 struct wyy 12 { 13 int to,va; 14 }; 15 vector<wyy>edge[MAXN]; 16 void init() 17 { 18 memset(v,0,sizeof(v)); 19 memset(f,0,sizeof(f)); 20 memset(dis,0,sizeof(dis)); 21 memset(deep,0,sizeof(deep)); 22 for(int i=1;i<MAXN;i++) 23 edge[i].clear(); 24 ans=0; 25 } 26 void dfs(int now,int fa)//计算各子树大小。。。。。。。。 27 { 28 int size=edge[now].size(); 29 f[now]=1; 30 for(int i=0;i<size;i++) 31 { 32 int to=edge[now][i].to,va=edge[now][i].va; 33 if(to!=fa&&v[to]==0)//不能搜到上头,不能往回搜。。。。。。 34 { 35 dfs(to,now); 36 f[now]+=f[to]; 37 } 38 } 39 //cout<<now<<" "<<f[now]<<endl; 40 } 41 void findroot(int now,int fa,int all)//找重心 42 { 43 int size=edge[now].size(); 44 int nowmax=all-f[now];//nowmax表示,选择当前点为根时的最大子树大小 45 for(int i=0;i<size;i++) 46 { 47 int to=edge[now][i].to,va=edge[now][i].va; 48 if(to!=fa&&v[to]==0)//不能搜到上头,不能往回搜。。。。。。 49 { 50 nowmax=max(nowmax,f[to]); 51 findroot(to,now,all); 52 } 53 } 54 if(nowmax<stand) 55 { 56 stand=nowmax; 57 newroot=now; 58 } 59 } 60 void getdis(int now,int fa)//计算以该重心为根的树,其余各点到根的距离 61 //边求,边存入数组!!!!!!!!!!!!!!! 62 { 63 int size=edge[now].size(); 64 //if(dis[now]!=0)不要自以为是地去掉零, 65 //0也要算进去!!!!!! 因为存在根到节点的距离 66 deep[++last]=dis[now]; 67 for(int i=0;i<size;i++) 68 { 69 int to=edge[now][i].to,va=edge[now][i].va; 70 if(v[to]==0&&to!=fa) 71 { 72 dis[to]=dis[now]+va; 73 getdis(to,now); 74 } 75 } 76 } 77 int calc(int nowroot,int basic)//每个距离的基准值 78 { 79 int i,j,ans2; 80 dis[nowroot]=basic; 81 last=0;//从头开始 82 getdis(nowroot,0); 83 sort(deep+1,deep+1+last); 84 // for(i=1;i<=last;i++) 85 // cout<<deep[i]<<" "; 86 87 //尺取法要对着数列模拟,把单调性想清楚。 88 i=1,j=last,ans2=0; 89 while(i<j) 90 { 91 // cout<<"i="<<i<<endl; 92 // cout<<"j="<<j<<endl; 93 //if(dis[i]+dis[j]<=k)//数组名错啦。。。。。。 94 if((deep[i]+deep[j])<=k)//对于重要的变量,如k,必须使用全局变量。输入的时候就要考虑清楚。 95 { 96 ans2+=j-i; 97 //cout<<ans2<<" "; 98 i++; 99 } 100 else j--; 101 } 102 // cout<<"ans2="<<ans2<<endl; 103 return ans2;//局部变量和全局变量不可重名…………………………………… 104 } 105 void work(int froot)//工作总流程,falseroot为假的根 106 //计算假根,以及搜索时,不能搜到上头,不能往回搜。。。。。。 107 { 108 dfs(froot,0);//求各子树大小。 109 stand=inf;// 各子树最大值 的最小值 110 findroot(froot,0,f[froot]); //找重心 111 //做自己! 112 v[newroot]=1;//有改动 113 ans+=calc(newroot,0);//计算总结果 114 //cout<<froot<<" "<<newroot<<" "<<ans<<endl; 115 int size=edge[newroot].size(); 116 117 for(int i=0;i<size;i++) 118 { 119 int to=edge[newroot][i].to,va=edge[newroot][i].va; 120 if(v[to]==0) 121 { 122 ans-=calc(to,va); 123 //cout<<to<<" "<<ans<<endl; 124 int nowlast=last,nowroot=newroot,nowstand=stand; 125 126 work(to); 127 //递归中,不要乱用全局变量,实在要用,必须回溯。。。。 128 //全局变量要回溯!!!!!!!!!!!!!!! 129 last=nowlast; 130 newroot=nowroot; 131 stand=nowstand; 132 } 133 } 134 } 135 int main() 136 { 137 ios::sync_with_stdio(false); 138 while(1) 139 { 140 cin>>n>>k; 141 if(n==0) 142 break; 143 init();//最后看着数组重新补充 144 for(int i=1;i<n;i++) 145 { 146 int u,v,l; 147 cin>>u>>v>>l; 148 edge[u].push_back((wyy){v,l}); 149 edge[v].push_back((wyy){u,l}); 150 } 151 work(1); 152 printf("%d\n",ans); 153 } 154 return 0; 155 }



