CF 1249F Maximum Weight Subset - 树形DP

CF 1249F Maximum Weight Subset

题目链接：CF 1249F Maximum Weight Subset CF 1249F Maximum Weight Subset

算法标签: 树、深搜、树形DP

题目描述：

给定一棵含 \(n\) 个节点的树，每个节点含一个点权 \(a[i]\) 。现在请你选出一些节点，使得这些节点的权值和最大并且这些节点中任意两个节点的距离都 \(>k\) 。并输出这个最大的权值。

输入第一行含两个整数 \(n,k\) ，之后是 \(n\) 个整数 \(a[i]\) ，之后是 \(n-1\) 行，每行两个整数，描述树的每条边。

题解：

树形DP

（CF div3最后一题很喜欢DP？？？？？ 逃~）

感觉上挺神仙的一道题，这个考场上应该是真的想不到………………

也是研究了小半天官方题解搞明白了。

下面开始正题：

---

我们设这棵树有根并且根是\(1\) ，之后来考虑以什么状态完成DP：

设\(dp[pos][dep]\)表示在\(pos\)的子树中符合条件的最大权值点集的权值和，并且保证这个最大权值点集中深度最小的点的深度\(\ge dep\)。（不太好理解…………）

之后的思路就是：我们需要计算 \(pos\) 的所有子节点的 \(dp[~][~]\)，以此来更新 \(dp[pos][0\sim n]\)。

考虑当前的深度是 \(dep\) ，就有以下的两种想法：

• 如果 \(dep == 0\)，我们可以得到

  \(dp[pos][dep] = val[pos]+\sum_{to \in children(pos)}dp[to][max(0, k - dep - 1)]\)，

• 如果 \(dep!=0\)，则可以得到 (\(to \in children(pos)~~~to \neq now\))

  \(dp[pos][dep]=max\{dp[pos][dep],dp[to][dep-1]+\sum_{now \in children(pos)}dp[now][max(dep-1,k-dep-1)]\}\)

之后我们要明确一个问题，在这其中我们包含着 \(k-dep-1\) 的计算，其实这里的 \(k = k_{初始}+1\) ，原因就是这里的计算保证的是每一个选择到的点都要与当前点的距离 \(\gt k\)，而不是 \(\ge k\)。

上图理解一下：

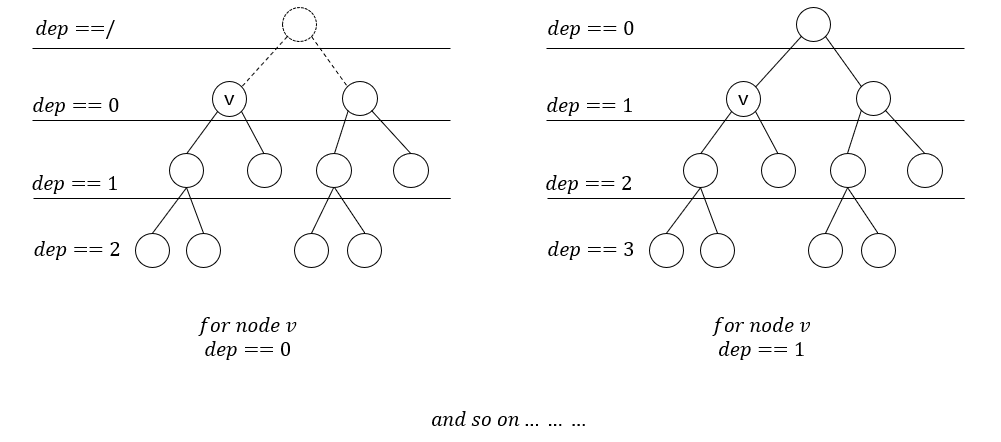
扔到整棵树里边：

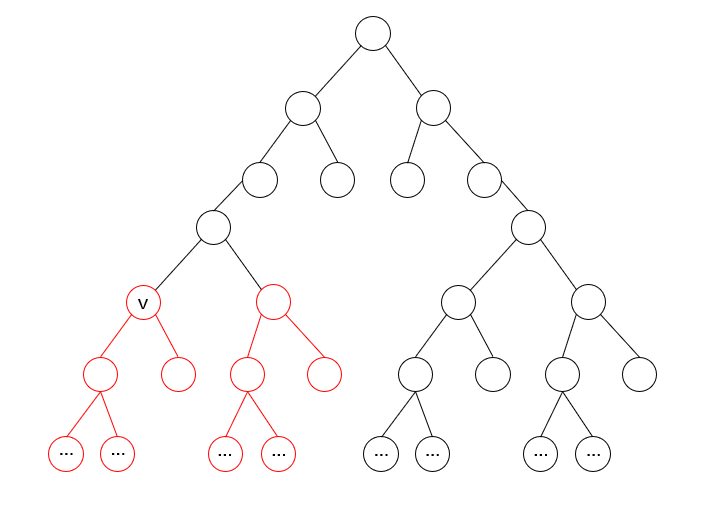
下面看代码：

AC代码

#include <bits/stdc++.h>

using namespace std;

const int N = 210;

vector <int> e[N];

int n, k, val[N];

int dp[N][N];

void add(int x, int y) {
	e[x].push_back(y);
	e[y].push_back(x);
}

void dfs(int pos, int pre) {
	dp[pos][0] = val[pos];
	for (int i = 0; i < (int)e[pos].size(); i ++ ) {
		int to = e[pos][i];
		if (to != pre) {
			dfs(to, pos);
		}
	}
	for (int dep = 0; dep < N; dep ++ ) {
		if (dep == 0) {
			for (int i = 0; i < (int)e[pos].size(); i ++ ) {
				int to = e[pos][i];
				if (to != pre) {
					dp[pos][dep] += dp[to][max(0, k - dep - 1)];
				}
			}
		}
		else {
			for (int i = 0; i < (int)e[pos].size(); i ++ ) {
				int to = e[pos][i];
				if (to == pre) {
					continue ;
				}
				int dis = dp[to][dep - 1];
				for (int i = 0; i < (int)e[pos].size(); i ++ ) {

					int now = e[pos][i];
					if (now == to || now == pre) {
						continue ;
					}
					dis += dp[now][max(dep - 1, k - dep - 1)];
				}
				dp[pos][dep] = max(dp[pos][dep], dis);
			}
		}
	}
	for (int dep = N - 1; dep > 0; dep -- ) {
		dp[pos][dep - 1] = max(dp[pos][dep - 1], dp[pos][dep]);
	}
}

int main() {
	scanf("%d%d", &n, &k);
	k ++ ;
	for (int i = 1; i <= n; i ++ ) {
		scanf("%d", &val[i]);
	}
	for (int i = 1; i <= n - 1; i ++ ) {
		int a, b;
		scanf("%d%d", &a, &b);
		add(a, b);
	}
	dfs(1, 0);
	cout << dp[1][0] << endl;
	return 0;
}