CF 796C Bank Hacking - 图论、思维
CF 796C Bank Hacking
题目链接:洛谷 CF796C Bank Hacking CF796C Bank Hacking
算法标签: 思维、图论
题目
题目描述
Although Inzane successfully found his beloved bone, Zane, his owner, has yet to return. To search for Zane, he would need a lot of money, of which he sadly has none. To deal with the problem, he has decided to hack the banks.
There are \(n\) banks, numbered from \(1\) to \(n\) . There are also \(n-1\) wires connecting the banks. All banks are initially online. Each bank also has its initial strength: bank \(i\) has initial strength \(a_{i}\) .
Let us define some keywords before we proceed. Bank \(i\) and bank \(j\) are neighboring if and only if there exists a wire directly connecting them. Bank \(i\) and bank \(j\) are semi-neighboring if and only if there exists an online bank \(k\) such that bank \(i\) and bank \(k\) are neighboring and bank \(k\) and bank \(j\) are neighboring.
When a bank is hacked, it becomes offline (and no longer online), and other banks that are neighboring or semi-neighboring to it have their strengths increased by \(1\) .
To start his plan, Inzane will choose a bank to hack first. Indeed, the strength of such bank must not exceed the strength of his computer. After this, he will repeatedly choose some bank to hack next until all the banks are hacked, but he can continue to hack bank \(x\) if and only if all these conditions are met:
- Bank \(x\) is online. That is, bank \(x\) is not hacked yet.
- Bank \(x\) is neighboring to some offline bank.
- The strength of bank \(x\) is less than or equal to the strength of Inzane's computer.
Determine the minimum strength of the computer Inzane needs to hack all the banks.
给定一棵带点权树,选出一个最佳的根节点,使得根节点的点权不变,它的儿子点权加\(1\),其余点点权加\(2\),并使最大点权最小,输出这个最小的最大点权
输入格式
The first line contains one integer \(n\) ( \(1<=n<=3·10^{5}\) ) — the total number of banks.
The second line contains nn integers \(a_{1},a_{2},...,a_{n} ( -10^{9}<=a_{i}<=10^{9} )\) — the strengths of the banks.
Each of the next \(n-1\) lines contains two integers \(u_{i}\) and \(v_{i}\) ( \(1<=u_{i},v_{i}<=n , u_{i}≠v_{i}\) ) — meaning that there is a wire directly connecting banks \(u_{i}\) and \(v_{i}\) .
It is guaranteed that the wires connect the banks in such a way that Inzane can somehow hack all the banks using a computer with appropriate strength.
输出格式
Print one integer — the minimum strength of the computer Inzane needs to accomplish the goal.
输入输出样例
输入 #1
5
1 2 3 4 5
1 2
2 3
3 4
4 5
输出 #1
5
输入 #2
7
38 -29 87 93 39 28 -55
1 2
2 5
3 2
2 4
1 7
7 6
输出 #2
93
输入 #3
5
1 2 7 6 7
1 5
5 3
3 4
2 4
输出 #3
8
说明/提示
In the first sample, Inzane can hack all banks using a computer with strength 55 . Here is how:
- Initially, strengths of the banks are \([1,2,3,4,5]\) .
- He hacks bank \(5\) , then strengths of the banks become \([1,2,4,5,-]\) .
- He hacks bank \(4\) , then strengths of the banks become \([1,3,5,-,-]\) .
- He hacks bank \(3\) , then strengths of the banks become \([2,4,-,-,-]\) .
- He hacks bank \(2\) , then strengths of the banks become \([3,-,-,-,-]\) .
- He completes his goal by hacking bank \(1\) .
In the second sample, Inzane can hack banks \(4\) , \(2\) , \(3\) , \(1\) , \(5\) , \(7\) , and \(6\) , in this order. This way, he can hack all banks using a computer with strength \(93\) .
题解:
思维
很卡人的思维题………………
首先根据题意,画画图,我们会发现答案仅有三种情况:
- \(ans~=~val_{max}\)
- \(ans~=~val_{max} + 1\)
- \(ans~=~val_{max} + 2\)
所以考虑一下下面的这些情况:
NO.1
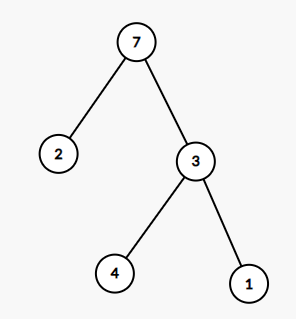
NO.2
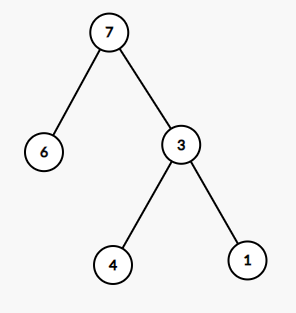
NO.3
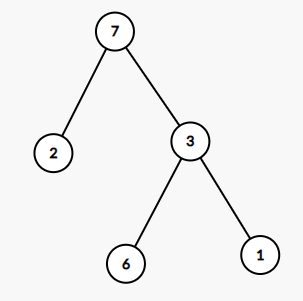
我们会发现,对于这几种情况,他们共同的特点是:
- \(val~=~val_{max}\)的点只有一个
之后我们会找出在这种情况下的几种答案:
- 当不存在\(val~=~val_{max}-1\)的点的时候,答案一定是\(ans~=~val_{max}\)
- 当存在\(val=val_{max}-1\)的点时,如果所有\(val~=~val_{max}-1\)的点都是\(val~=~val_{max}\)的点的子节点,答案是\(ans~=~val_{max}\),否则\(ans~=~val_{max} + 1\)
NO.4
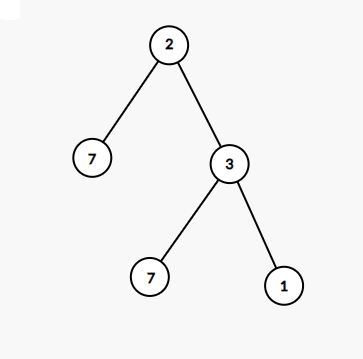
NO.5
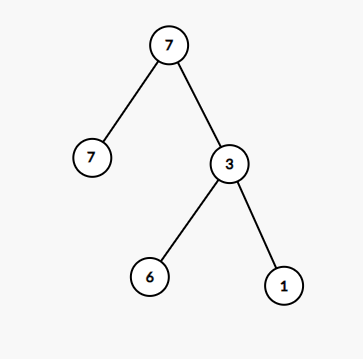
再看这两种情况,我们会发现:
- 这时\(val~=~val_{max}\)的点不只有一个(\(\ge2\))
之后我们可以得出在这种情况下的答案:
- 如果所有\(val~=~val_{max}\)的点都连在一个其他点上或者连在一个\(val~=~val{max}\)的点上,答案为\(ans~=~val_{max}+1\)
- 否则答案为\(ans~=~val_{max}+ 2\)
那么我们最终整理一下这些情况:
- 当\(val~=~val_{max}\)的点只有一个的时候:
- 如果\(val~=~val_{max}-1\)的点不存在,\(ans~=~val_{max}\)
- 如果\(val~=~val_{max}-1\)的点存在,且这个点是\(val~=~val_{max}\)的那个点的子节点,\(ans~=~val_{max}\)
- 如果\(val~=~val_{max}-1\)的点存在,且这个点不是\(val~=~val_{max}\)的点的子节点,\(ans~=~val_{max}+1\)
- 当\(val=val_{max}\)的点有多个的时候:
- 如果所有\(val~=~val_{max}\)的点都是一个点的子节点,\(ans~=~val_{max}+1\)
- 如果一个\(val~=~val_{max}\)的点的子节点中包含所有其他\(val~=~val_{max}\)的点, \(ans~=~val_{max}+1\)
- 如果不满足以上两种情况,\(ans~=~val_{max}+2\)
最终按照这个模拟即可。注意细节和数据范围。
AC代码
#include <bits/stdc++.h>
using namespace std;
#define setI(x) freopen(x".in", "r", stdin);
#define setO(x) freopen(x".out", "w", stdout);
#define setIO(x) setI(x) setO(x)
typedef long long ll;
const int N = 300010;
const int inf = 0x3f3f3f3f;
int n;
ll val[N], mx;
int totmx, totse, tmp;
int tot, head[N], nxt[N << 1], to[N << 1];
void add(int x, int y) {
to[ ++ tot] = y;
nxt[tot] = head[x];
head[x] = tot;
}
int main() {
// setIO("tree");
scanf("%d", &n);
mx = -inf;
for (int i = 1; i <= n; i ++ ) {
scanf("%I64d", &val[i]);
if (val[i] > mx) {
mx = val[i];
tmp = i;
}
}
for (int i = 1; i <= n; i ++ ) {
if (val[i] == mx) {
totmx ++ ;
}
if (val[i] == mx - 1) {
totse ++ ;
}
}
for (int i = 1; i < n; i ++ ) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
if (totmx == 1) {
if (totse == 0) {
cout << mx << endl;
return 0;
}
else {
int now = 0;
for (int i = head[tmp]; i; i = nxt[i]) {
if (val[to[i]] == mx - 1) {
now ++ ;
}
}
if (now == totse) {
cout << mx << endl;
return 0;
}
else {
cout << mx + 1 << endl;
return 0;
}
}
}
if (totmx >= 2) {
for (int i = 1; i <= n; i ++ ) {
int cnt = 0;
for (int j = head[i]; j; j = nxt[j]) {
int now = to[j];
if (val[now] == mx) {
cnt ++ ;
}
}
if (val[i] != mx && cnt == totmx) {
cout << mx + 1 << endl;
return 0;
}
if (val[i] == mx && cnt == totmx - 1) {
cout << mx + 1 << endl;
return 0;
}
}
}
cout << mx + 2 << endl;
return 0;
}


