CF 358D Dima and Hares - DP

CF 358D Dima and Hares

题目链接：洛谷 CF 358D Dima and Hares CF 358D Dima and Hares

算法标签: DP、思维

题目描述：

\(N\)个物品排成一排,按照一定顺序将所有物品都拿走，如果拿走某个物品时相邻两个物品都没有被拿过，那么得到的价值为\(a_i\)；如果相邻的两个物品有一个被拿过（左右无所谓），那么得到的价值为\(b_i\)；如果相邻的两个物品都被拿走了，那么对应价值为\(c_i\)。问能够获得的最高价值为多少。

题解：

DP

看到题之后，第一反应就是贪心或者DP。仔细看一看，果断pass掉贪心的想法。

之后我们会发现这道题的DP有一些很难逾越的坑（导致我第一份代码写了140行还假了…………）：

• 每一个点的决策会改变前后两点的答案，前后两点的决策也会影响到当前点的答案
• 第一个点和最后一个点只能选择\(a\)或者\(b\)。

对于第一个问题，我们就要考虑如何搞方程才能满足这个条件。

如果每次都考虑当前点为中间点的话，的确很直接，很清晰，但是怎么同时对前后更改，（如果前后更改还会涉及到其它点的更改），这显然是实现不了的。

那么我们更换思路，考虑每一次遍历到的当前点是三个点中的最后一个，上图理解：

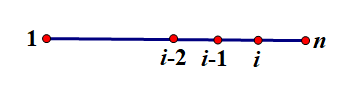
这样我们可以搞出来一个DP状态：

\(dp[i][1]\)表示先选择\(i - 1\)， 后选择\(i\)，可以得到的前\(i - 1\)的最大答案。

\(dp[i][0]\)表示先选择\(i\)，后选择\(i-1\)可以得到前\(i - 1\)的最大答案。

那么转移方程：

\(dp[i][1] = max(dp[i - 1][1] + b[i-1], dp[i - 1][0] + a[i-1])\)

\(dp[i][0] = max(dp[i - 1][1] + c[i-1], dp[i - 1][0] + b[i-1])\)

上图理解：

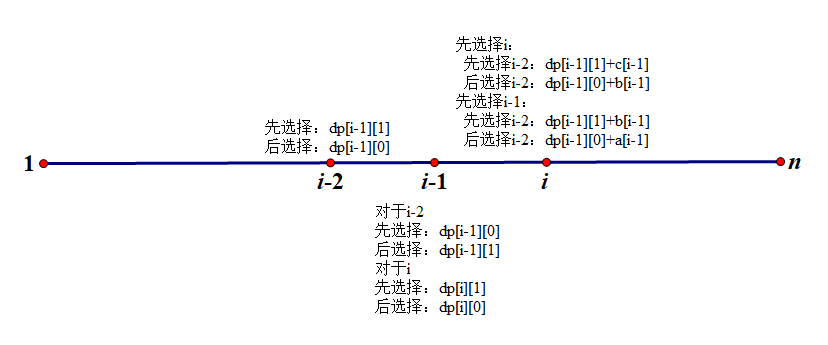
这样第一个问题就解决了，那么怎么解决第二个问题：\(1\)号点和\(n\)号点。

首先因为每次取最大值，不妨设所有的\(dp[~][~]~=~-inf\)。

之后对于第一个点，由于它前边没有点，所以一定会先取这个点：\(dp[1][0]=0\)

对于最后一个点，由于他后边没有点，那么我们假设后边有一个点（由于状态当中\(dp[i]\)存放的是\(1 \sim i-1\)的答案），并且对于这个多出来的点来说，一定是先取\((n+1)-1\)这个点，所以在第\(n\)个点的答案自然就是\(dp[n+1][1]\)

现在状态有了，初值有了，转移方程有了，答案也有了，直接写dp就解决了。

AC代码

#include <bits/stdc++.h>

using namespace std;

#define setI(x) freopen(x".in", "r", stdin);

#define setO(x) freopen(x".out", "w", stdout);

#define setIO(x) setI(x) setO(x);

const int N = 100100;

typedef long long ll;

int n, a[N], b[N], c[N];

ll dp[N][2];

void rd() {
	for (int i = 1; i <= n; i ++ ) {
		scanf("%d", &a[i]);
	}
	for (int i = 1; i <= n; i ++ ) {
		scanf("%d", &b[i]);
	}
	for (int i = 1; i <= n; i ++ ) {
		scanf("%d", &c[i]);
	}
}

int main() {
	// setIO("cow");
	scanf("%d", &n);
	rd();
	memset(dp, -0x3f, sizeof dp);
	dp[1][0] = 0;
	for (int i = 2; i <= n + 1; i ++ ) {
		dp[i][0] = max(dp[i - 1][0] + b[i - 1], dp[i - 1][1] + c[i - 1]);
		dp[i][1] = max(dp[i - 1][0] + a[i - 1], dp[i - 1][1] + b[i - 1]);
	}
	cout << dp[n + 1][1] << endl;
	return 0;
}