洛谷 P5520 [yLOI2019] 青原樱 - 组合数学

洛谷 P5520 [yLOI2019] 青原樱

题目链接：洛谷 P5520 [yLOI2019] 青原樱

算法标签: 组合数学

题目

题目背景

星川之下皆萤火尘埃

我独行在人潮你天真而待

相遇若是借丹青着色

青原上 绯樱如海

——银临《青原樱》(Cover 人衣大人)

题目描述

有一个邮递员要送东西，邮局在节点1.他总共要送N-1样东西，其目的地分别是2~N。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有M条道路，通过每条道路需要一定的时间。这个邮递员每次只能带一样东西。求送完这N-1样东西并且最终回到邮局最少需要多少时间。

输入格式

扶苏是一个非常喜欢边听古风鸽边写数学题的人，因此这道题其实是个五三原题。

扶苏希望重现青原上樱花盛开的景色，于是他准备了很多互不相同樱花树幼苗，准备种成一行。

这一行中，一共有 \(n\) 个位置可以种下樱花，而扶苏准备了 \(m\) 支幼苗。由于樱花盛放时对左右空间需求非常大，所以樱花不能紧挨着种植，也就是任意两支幼苗之间必须至少存在一个不种花的空位置。

按照这种方式种花并不难，但是令扶苏感到好奇的是一共有多少合法的方案让他把这 \(m\) 支幼苗都种下去。一个方案是合法的当且仅当他满足上一段中叙述的要求。如果我们将花按照 \(1,~2,~3~\dots~m\) 编号，两种方案不同当且仅当被选择种花的位置不同或从左向右数花的编号序列不同。

为了避免输出过大，答案对一个参数 \(p\) 取模。

【数据规模】

每个输入文件中有且仅有一组测试数据。

测试数据只有一行四个数字，依次代表 \(type,~n,~m,~p\)，其中 \(type\) 是一个帮助你判断测试点类型的参数，会在数据范围中说明。

输出格式

输出一行一个数字，代表答案对 \(p\) 取模的结果。

输入输出样例

输入 #1

1 3 2 19260718

输出 #1

2

说明/提示

样例解释

一共有 2 个樱花幼苗， 3 个种花的位置，如果给幼苗编号为 1, 2，位置编号为 1, 2, 3，那么两种方案分别如下：

数据范围与约定

本题采用多测试点捆绑测试

各子任务的数据范围与特殊性质如下表所示

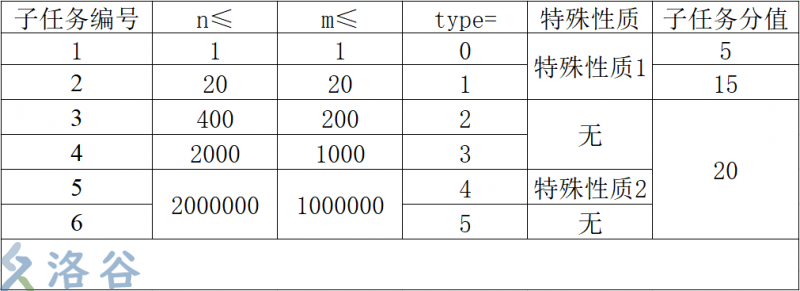
特殊性质1：保证对应测试点的实际方案数(在取模前)不超过 \(10^6\)

特殊性质2：保证 pp 是一个质数。

对于 \(100\%\) 的数据，保证 \(1 \leq p \leq 10^9\)，\(1 \leq m \leq \lceil \frac{n}{2} \rceil\)

提示：\(type\) 可以帮助你快速的判断子任务编号。

题解：

部分内容参考出题人题解：A [yLOI2019] 青原樱

对于这六道题的子任务出题人给出了分别的六种做法（我写的正解，即最后一种），大致如下：

子任务1（5 pts）：

由于\(n = m = 1\)，所以方案数显然为\(1\)，但是要注意\(p = 1\)的情况时候答案为\(0\)。

子任务2（15 pts）：

暴搜，保证搜索树上每个节点的情况都是合法的且后代一定存在一种以上的合法方案即可（原文）。总复杂度为\(O(n \times ans)\)的。

子任务3（20 pts）：

DP做法，设\(f[i][j]\)为第\(i\)个幼苗放在第\(j\)个位置的方案数。

转移方程： \(f_{i, j} = \sum_{k = 0}^{j - 2}f_{i - 1,k}\)

初始化的时候\(f[0][0] = 1\)，但是题目中要求幼苗互不相同，那么答案需要\(\times m!\)。

总复杂度为\(O(n^2m)\)。

子任务4（20 pts）：

对于子任务3的转移方程来说，我们可以通过维护前缀的方式将转移降为\(O(1)\)，所以总复杂度为\(O(nm)\)。

子任务5（20 pts）：

DP做法最低复杂度为\(O(nm)\)，显然在这道题是不满足全部数据的，那么我们采取组合数学的方式。

总的方案分为2类：A.第n个位置没有树苗 B：第n个位置有树苗。

A类：

我们把每个树苗与其相邻的空位看做一个物体，那么问题变成了在（n-m）个位置中选择m个位置放置m个物品，那么共有\(C_{n-m}^{m}\)，又因为树苗各不相同，所以最终的方案数为\(m! \times C_{n-m}^m\) .

B类：

对于前面的(m - 1)个树苗，我们把它们与它们相邻的空位看做一个物体，那么就是在(n - m)个位置，选择(m-1)个位置，那么方案数为\(C_{n - m}^{m - 1}\)。而最后一个树苗共有m个情况，所以总方案数为\(m! \times C_{n-m}^{m-1}\)，而当p为质数时候\(O(n)\)处理逆元，\(O(n)\)计算即可。

子任务6（20pts）：

当我们整理一下式子就可以发现，对于第一种情况来说，\(m! \times C_{n-m}^{m} = A_{n-m}^{m}\)；对于第二种情况来说，\(m! \times C_{n-m}^{m-1} = m \times A_{n-m}^{m-1}\)，又因为两种情况加和\(A_{n-m}^{m}+m\times A_{n-m}^{m-1} = A_{n-m+1}^{m}\)，最终得出的时间复杂度为\(O(n)\)。

附：一些对于组合数学的基本公式：

1. 排列：从n个不同的元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列
   从n个数中取出m个数进行排列的方案数用符号A(n,m)表示
   公式：A(n,m)=n(n-1)(n-2)...(n-m+1)=n!/(n-m)!
2. 组合：从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数
   从n个数中取出m个数的方案数用符号C(n,m)表示
   公式：C(n,m)=A(n,m)/A(m,m)=n!/(m!(n-m)!)

AC代码

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

int type, p, n, m;
ll ans = 1ll;

int main()
{

	scanf("%d%d%d%d", &type, &n, &m, &p);
	for (int i = n - 2 * m + 2; i <= n - m + 1; i ++ )
	{
		ans = (ans * 1ll * i) % p;
	}
	printf("%lld", ans);
	return 0;
}