HZNU Training 22 for Zhejiang Provincial Competition 2020

F - Instability

题意：一张图，求有多少个集合，包含三元环或者补三元环，

考虑 如下性质

 

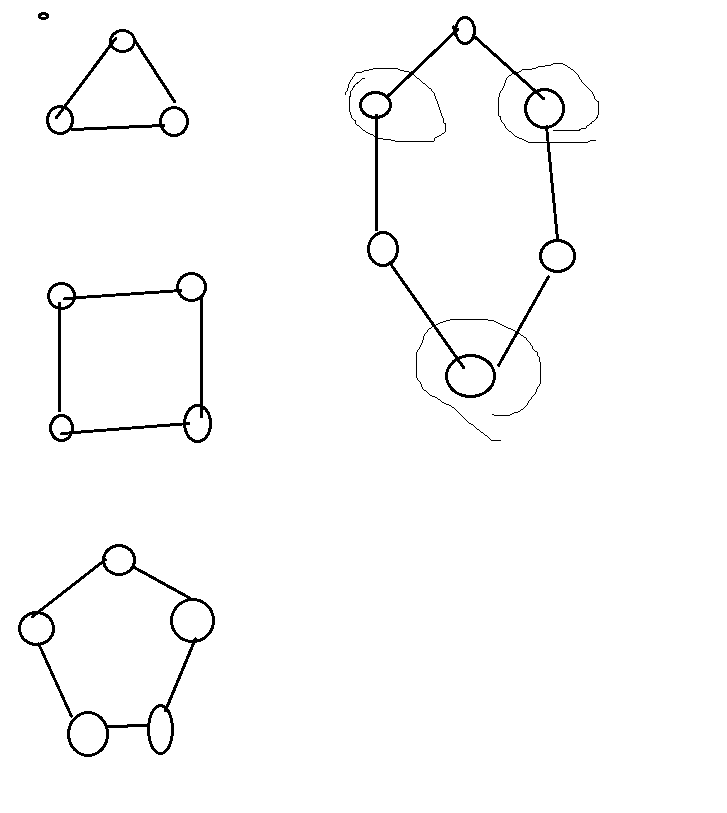
Ramsey定理--世界上任意6个人中，总有3个人相互认识，或互相皆不认识。

 当集合大小大于6时，发生了变化，一定满足，至少三个互不相连，或者互相连接，

记录一下6元以上的关系，算出组合数，然后暴力出 n = 5，n=4，n = 3的情况。

#include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
#define pb push_back
#define fi first
#define se second
const int maxn=100;
const int N=70;
const int inf=0x3f3f3f3f;
int gp[N][N];
const ll MOD=1e9+7;
long long C[200][200];
int n,m;
void get_C(){
    C[0][0] = 1;
    for(int i=1;i<=maxn;i++)
    {
        C[i][0] = 1;
        for(int j=1;j<=i;j++)
            // C[i][j] = C[i-1][j]+C[i-1][j-1];
            C[i][j] = (C[i-1][j]+C[i-1][j-1])%MOD;
    }
}
void init(){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            gp[i][j]=0;
        }
    }
}
bool ok(int a,int b,int c){
    if(gp[a][b]&&gp[a][c]&&gp[b][c])return 1;
    else if(!gp[a][b]&&!gp[a][c]&&!gp[b][c])return 1;
    return 0;
}
bool ok(int a,int b,int c,int d){
    if(ok(a,b,c))return 1;
    if(ok(a,b,d))return 1;
    if(ok(b,c,d))return 1;
    if(ok(a,c,d))return 1;
    return 0;
}
bool ok(int a,int b,int c,int d,int e){
    if(ok(b,c,d,e))return 1;
    if(ok(a,d,c,e))return 1;
    if(ok(a,b,d,e))return 1;
    if(ok(a,b,c,e))return 1;
    if(ok(a,b,c,d))return 1;
    return 0;
}
int main(){
    get_C();
    int t,kase=0;
    scanf("%d",&t);
    while(t--){
    scanf("%d %d",&n,&m);
        init();
    for(int i=1,u,v;i<=m;i++){
        scanf("%d %d",&u,&v);
        gp[u][v]=gp[v][u]=1;
    }
    ll cnt=0;
    if(n>=6){
    for(int i=6;i<=n;i++)cnt=(cnt+C[n][i])%MOD;
    }

    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            for(int k=j+1;k<=n;k++){
                if(ok(i,j,k))cnt++;
            }
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            for(int k=j+1;k<=n;k++){
                for(int l=k+1;l<=n;l++){
                if(ok(i,j,k,l))cnt++;
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            for(int k=j+1;k<=n;k++){
                for(int l=k+1;l<=n;l++){
                    for(int p=l+1;p<=n;p++){
                    if(ok(i,j,k,l,p))cnt++;
                    }
                }
            }
        }
    }

    cnt%=MOD;
    printf("Case #%d: %lld\n",++kase,cnt);
    }
    // system("pause");
    return 0;
}
// 除非枚举每一个集合，但这样复杂度O(n!)

G - Sequence I

暴力枚举即可

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N],b[N];
int main(){
    int t;
    scanf("%d",&t);
    int kase=0;
    while(t--){
        int n,m,p;
        scanf("%d %d %d",&n,&m,&p);
        for(int i=1;i<=n;i++)scanf("%d",&a[i]);
        for(int i=1;i<=m;i++)scanf("%d",&b[i]);
        int ans=0;
        for(int i=1;i+(m-1)*p<=n;i++){
            bool flag=1;
            for(int j=i;j<=i+(m-1)*p;j+=p){
                if(a[j]!=b[(j-i)/p+1]){flag=0;break;}
            }
            if(flag)ans++;
        }
        printf("Case #%d: %d\n",++kase,ans);
    }
    system("pause");
    return 0;
}
// E和I应该都是数论
// F:一张图n个点，求1到n不稳定子集个数，一个集合不稳定当且仅当他有一个子集，互不相连，或者两两相连