机器学习--决策树原理

概览

分类问题

eg：给定了一个餐厅的数据，决策是否需要等待；

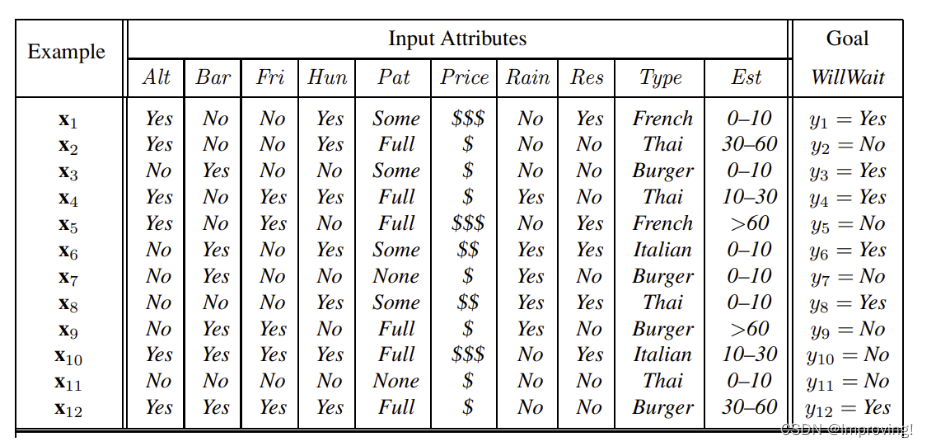
首先将特征属性split,假如先从Res开始，将value是Yes的分成一组，value是No的分成一组，也就是x1,x5,x6,x8,x10,x12值都是Yes，可以分成一组，然后在Res = Yes的组里继续分，假如第二次split的属性是Type，可以看出Type有五个不同值，再将这些值分成5个组，一直分到没有属性可分（也就是一组里面所有的属性均一致）为止。

split属性的顺序

根据确定性才划分分割的顺序。

计算确定性的方法（熵）

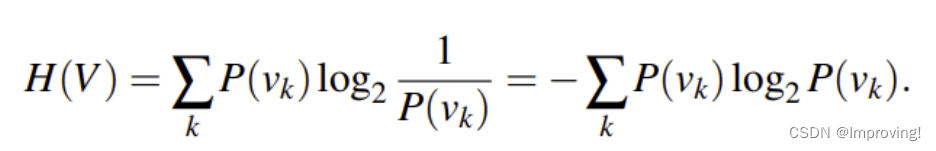
解释：
如果V是一个特征x1全部一致（按照x1分割）的样例点集合，有k个不同的特征对应值，P(Vk)就是y = Vk(y：特征所对应的值)的点的个数除以|V|。H(V)是所有特征值

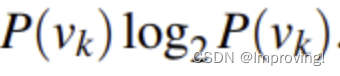
的加和。

如果只有两个值（如y = 是/否）,则可以表示为：

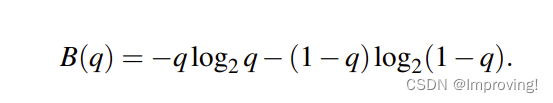
Hafter:这是综合考虑左节点和右节点的情况做出的加权平均值

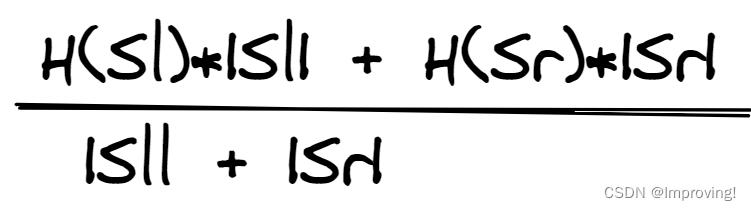
举例：

引入信息增益

信息量：选择split的好特征。
注：y表分类结果。
以餐厅为例：
Assume we have already performed a few node splits on our original restaurant dataset and we would like to further split a subset using the Type feature, which can take 5 distinct values. So the data points of that node will be split into 5 nodes which we will call E1,E2,E3,E4,E5. Each of those nodes Ek will have pk positive data points (y=yes) and nk negative ones (y=no). Furthermore, let p and n denote the number of positive and negative points of the original node before the split. Then the information gain of the feature Type is defined as follows ：

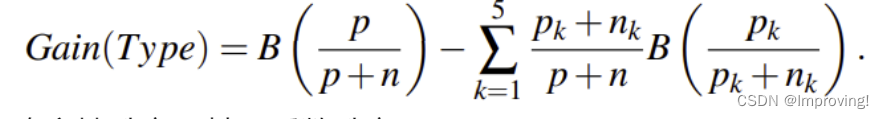
不确定性升高，信息增益升高。

流程伪代码

简易流程图：

建造决策树的具体方案（递归调用 形似二叉树）

如上图所示例子
首先设立一个集合S，包含了所有的样例点，选择根节点；建造叶子节点时或许需要从S中去除一部分节点，比如上图建立根节点Paltrons后，Patrons值为No的节点y值与其他特征值均相同，此时就可以将这些Patrons为No的节点从集合中去除。

具体过程

在节点处所有的特征值均相等且y也相等，就返回叶子节点；
如果不相等，选择一个最好的特征j，设置一个splitting value β，j有左右两个节点，左节点集合Sl里面是所有splitting value Xij < β，右节点集合Sr里面是
splitting value Xij >= β的节点集合。

选择最好split

1.尝试所有的拆分特征方法；
1.对于集合S,设J(S)为S损失函数；
3.选择J(Sr)+J(Sl)最小的方案；选择加权平均最小的方案（|Sr|J(Sr)+|Sl|J(Sl))/(|Sr|+|Sl|)

选择J(S)的方案

糟糕的方案

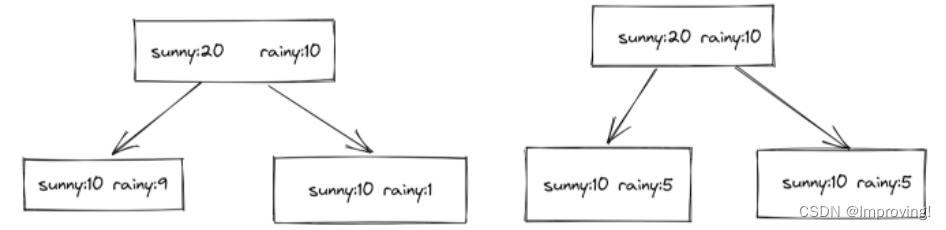
该方案将J(S)设置为其他所有值不为S的样例点的个数，上图是两种不同的split（根据不同的特征分割），需要计算J(sunny)，也就是如果按照sunny分割，特征值是sunny的都分在一起时的损失函数，左图左节点J(Sl) = 9, 右节点J(Sr) = 1,右图左节点J(Sl) = 5，右节点J(Sr) = 5，这时J(Sr)+J(Sl)都相等，加权平均右图更小，但是根据决策树分类原理，左边的更好（左边的右节点只需要再来一层就可以完全区分开sunny和rainy）。所有该方法不建议使用。

好的方案

算出H(S)，S节点为父节点，算出Hafter，选择H(S)-Hafter的值最大的一个方案。
还以上图为例，第一个图方案一计算：

H(Sl) =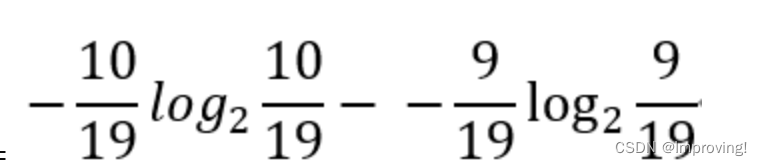

其余H算法相同，算出H(S) = 0.918,H(Sl) = 0.439,H(Sr) = 0.998.
Hafter = 0.793
算出H(S) - Hafter = 0.125.
方案二分割法：H(S) - Hafter = 0.(这种情况就是分割后并没有任何progress)
该方法可以选择出更好的split.

两方案比较

图像比较：

更好的方法

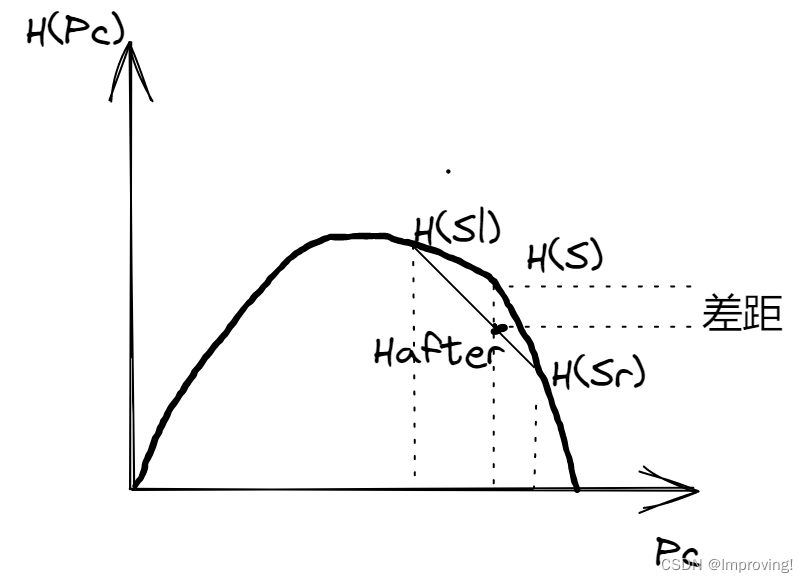
这种方法可以看出决策树的决策过程其实是不确定（熵）逐渐减小的过程，差距越大，熵减就越显著。这种方法做出的图像是严格的凹函数。

糟糕的方法

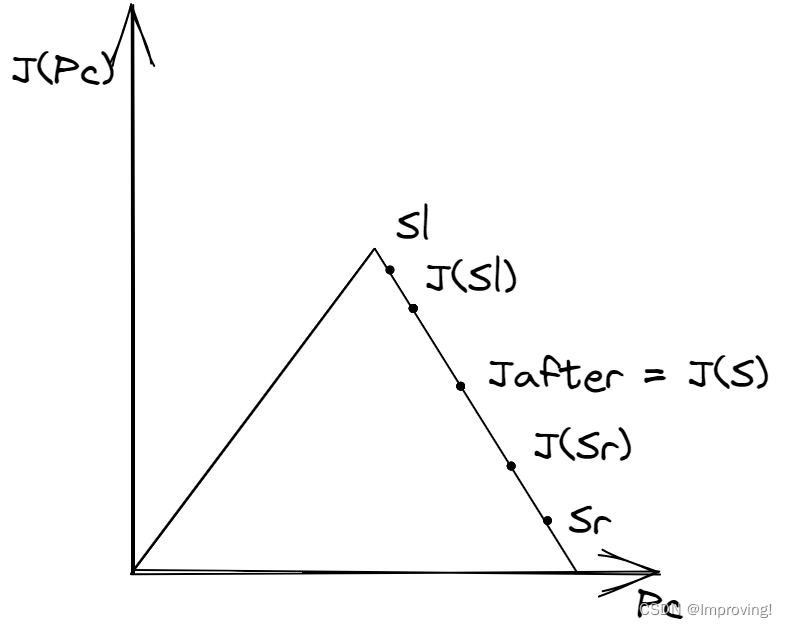
这种方法完全会出现上图的情况，改变Sl，Sr（也即改变了分割方法）差距仍是0，Jafter没有变化。
所以这个方法有时候不适用。

具体方案

选择split的好方法

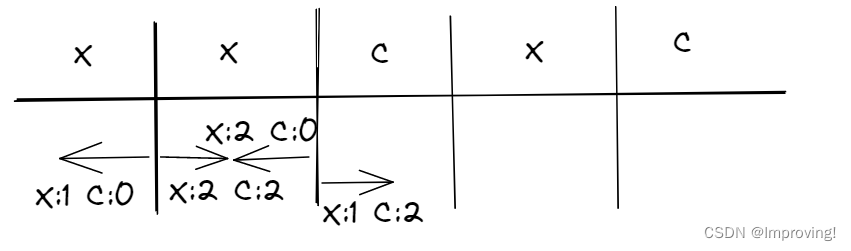
上例一共有四种分割，在第一处分割处从左到右扫描，可以获知右边的X有两个，C有两个，然后算出第一处分割的H,然后向右扫描剩下的split,扫描到X,左边的X数量+1，右边X - 1.这样只需要线性时间即可。

给测试样例分类

walk down tree，返回它的最后叶子节点的值。
注意：一直分割到单个叶子节点可能导致过拟合问题。