算法笔记——贪心算法
贪心算法就是通过局部最优达到全体最优的目的。下面用两道习题来说明贪心算法。贪心算法一般难以证明,所以在想到某个策略,又无法举出反例的情况下就可以采用贪心算法。
例题1:
现在他把他喜欢的电视节目的转播时间表给你,你能帮他合理安排吗?
输入
接下来n行,每行输入两个整数si和ei(1<=i<=n),表示第i个节目的开始和结束时间,为了简化问题,每个时间都用一个正整数表示。
当n=0时,输入结束。
输出
样例输入 Copy
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
0
样例输出 Copy
5
题目思路:
这是一个区间贪心的问题。上面的问题可以简化为区间不相交问题,给出n个开区间,从中选取最多的开区间,使得各个区间之间没有交集,用图形标识如下:
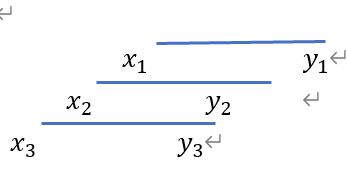
可以看出最上面一个区间即(x1,y1)有一部分与任何区间都不重合,与其他区间重合的另一部分又是三个区间中间最小的,根据题目要求,要求不重合区间数量最多,则应选择区间(x1,y1)。依此类推会观察到选择区间的原则为:左端点大的区间优先或者右端点小的区间优先。
代码实现:
#include <stdio.h> #include <stdlib.h> #include <math.h> struct node { int x; int y; }a[105]; int cmp(const void*p,const void*q){ return (*(int*)q-*(int*)p); } int main() { int n; while (1) { scanf("%d",&n); if(n==0){ return 0; } int s=0; for(int i=0;i<n;i++){ scanf("%d %d",&a[i].x,&a[i].y); } qsort(a,n,sizeof(a[0]),cmp); s++; int temp=a[0].x; for(int i=0;i<n;i++){ if(a[i].y<=temp){ s++; temp=a[i].x; } } printf("%d\n",s); } }
例题2:
You are given two arrays aa and bb of nn positive integers each. You can apply the following operation to them any number of times:
- Select an index ii (1≤i≤n1≤i≤n) and swap aiai with bibi (i. e. aiai becomes bibi and vice versa).
Find the minimum possible value of max(a1,a2,…,an)⋅max(b1,b2,…,bn)max(a1,a2,…,an)⋅max(b1,b2,…,bn) you can get after applying such operation any number of times (possibly zero).
The input consists of multiple test cases. The first line contains a single integer tt (1≤t≤1001≤t≤100) — the number of test cases. Description of the test cases follows.
The first line of each test case contains an integer nn (1≤n≤1001≤n≤100) — the length of the arrays.
The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤100001≤ai≤10000) where aiai is the ii-th element of the array aa.
The third line of each test case contains nn integers b1,b2,…,bnb1,b2,…,bn (1≤bi≤100001≤bi≤10000) where bibi is the ii-th element of the array bb.
For each test case, print a single integer, the minimum possible value of max(a1,a2,…,an)⋅max(b1,b2,…,bn)max(a1,a2,…,an)⋅max(b1,b2,…,bn) you can get after applying such operation any number of times.
3 6 1 2 6 5 1 2 3 4 3 2 2 5 3 3 3 3 3 3 3 2 1 2 2 1
18 9 2
In the first test, you can apply the operations at indices 22 and 66, then a=[1,4,6,5,1,5]a=[1,4,6,5,1,5] and b=[3,2,3,2,2,2]b=[3,2,3,2,2,2], max(1,4,6,5,1,5)⋅max(3,2,3,2,2,2)=6⋅3=18max(1,4,6,5,1,5)⋅max(3,2,3,2,2,2)=6⋅3=18.
In the second test, no matter how you apply the operations, a=[3,3,3]a=[3,3,3] and b=[3,3,3]b=[3,3,3] will always hold, so the answer is max(3,3,3)⋅max(3,3,3)=3⋅3=9max(3,3,3)⋅max(3,3,3)=3⋅3=9.
In the third test, you can apply the operation at index 11, then a=[2,2]a=[2,2], b=[1,1]b=[1,1], so the answer is max(2,2)⋅max(1,1)=2⋅1=2max(2,2)⋅max(1,1)=2⋅1=2.
题目思路:
题目意在计算两个数组中最大的数的乘积,要求该乘积最小,根据题意,我们要通过交换数字使得每一组的最大数字最小,两数组中的最大数字无论怎样交换都仍在需要相乘的两个数中,假设给出两个数组a、b,假设最大的数字在a中,那么就可以将b数组中比a组对应位置大的数字均交换,比如a数组为1 2 6 5 1 2,b数组为3 4 3 2 2 5,两个数组中最大的数是a数组的6,无论怎样交换6必然会被运算,所以我们现在的目标就是通过交换使得b数组中的最大数字最小,将b中所有小于a的数字交换,3大于1,将3与1交换,4比2大,将4与2交换......遍历b数组达到b组中的最大值最小的目的。
代码实现:
#include <stdio.h> int main() { int n; scanf("%d",&n); while(n--){ int m; scanf("%d",&m); int a[10005]={0},b[10005]={0}; int max1=0,max2=0,m1,m2; for(int i=0;i<m;i++){ scanf("%d",&a[i]); if(a[i]>max1){ max1=a[i]; m1=i; } } for (int i = 0; i < m; i++) { scanf("%d",&b[i]); if(b[i]>max2){ max2=b[i]; m2=i; } } int t,s,MAX=0; if(max1>=max2){ for(int i=0;i<m;i++){ if(a[i]<b[i]){ t=a[i];a[i]=b[i];b[i]=t; } if(b[i]>MAX) MAX=b[i]; } s=max1*MAX; } if(max1<max2){ for(int i=0;i<m;i++){ if(b[i]<a[i]){ t=a[i];a[i]=b[i];b[i]=t; } if(a[i]>MAX) MAX=a[i]; } s=max2*MAX; } printf("%d\n",s); } }
提交网址:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号