多项式计算1
单位根
引入
我们研究复数中特殊的一类数,即在复数范围内 \(x^n=1(n \in \N_+)\) 的根,它们称为单位根,方程为 \(n\) 则被称为 \(n\) 次单位根,记作 \(\omega_n\),由代数基本定理可知,\(n\) 次单位根共有 \(n\) 个,我们逆时针依次编号为 \(\omega_n^0,\cdots,\omega_n^{n-1}\),结合复数乘法的几何意义(模长相乘,辐角相加)可以知道单位根的模长皆为 \(1\),单位根 \(\omega_n^k\)辐角为 \(\dfrac {2k\pi}n\)。所以依据欧拉公式
下面是 \(8\) 次单位根的示例
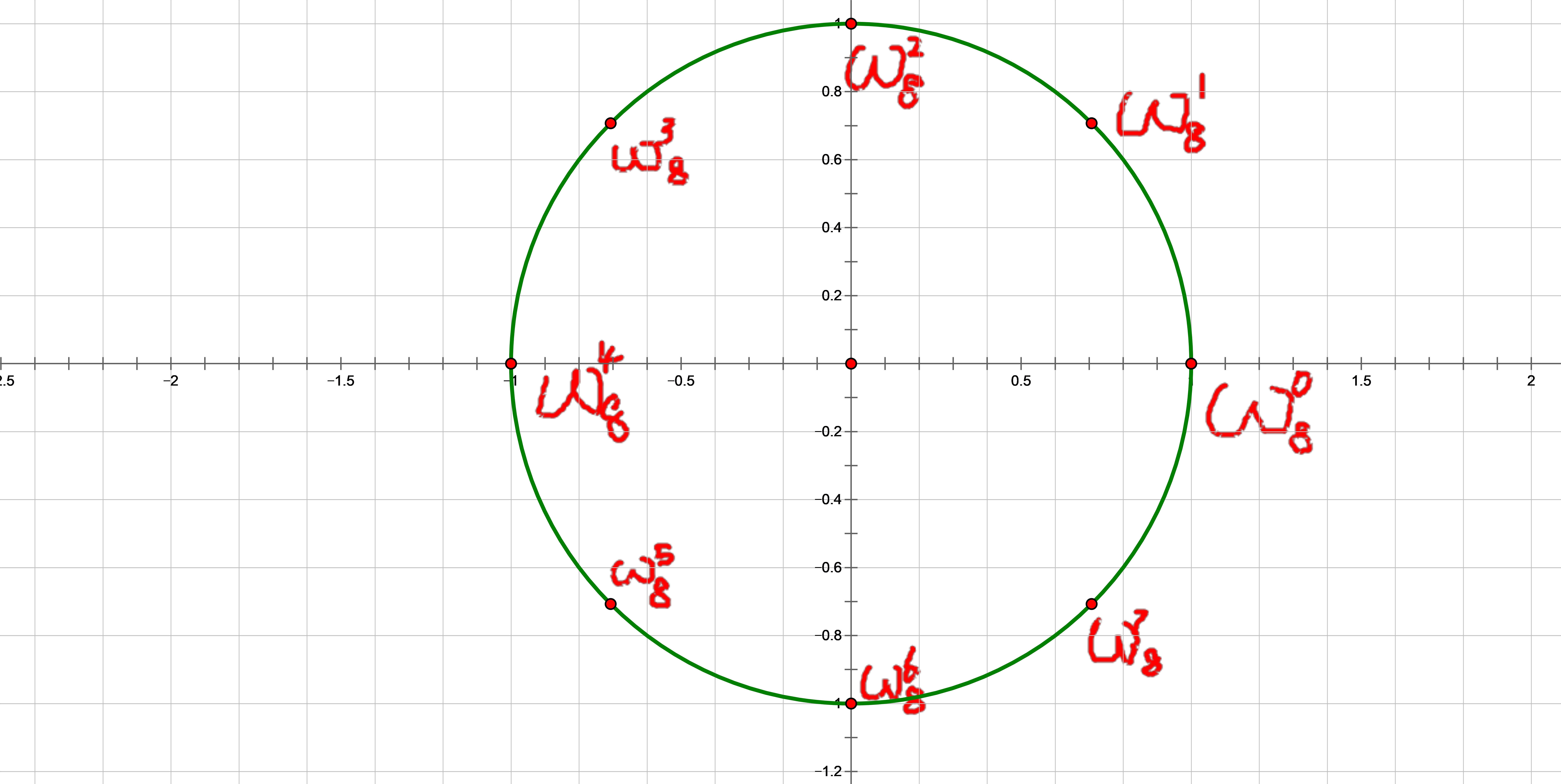
性质
根据其指数表达结合几何意义我们可以发现以下性质:
- 折半性质:
\(\texttt{Proof}:\;\omega_n^k=(\omega_n^1)^k=(\omega_{2n}^2)^k=\omega_{2n}^{2k}\)
- 对称性质:
\(\texttt{Proof}:\;\omega_{2n}^n=-1,\omega_{2n}^{k+n}=\omega_{2n}^k\times \omega_{2n}^n=-\omega_{2n}^k\)
- 求和性质:
\(\texttt{Proof}:\) 考虑等比数列求和,所以有
分类讨论
- 当 \(k=0\) 时,不能展开为等比数列形式,但因为 \(\omega_n^0=1\) 所以答案显然为 \(n\);
- 当 \(k\not=0\) 时,\(1-\omega_n^k\not=0\),\((\omega_n^k)^n=\omega_n^{nk}=\omega_1^k=1\),\(1-(\omega_n^k)^n=0\),所以原式为 \(0\);
单位根反演
结合上面的求和性质,我们可以写出下列反演
\(\texttt{FFT}\)
卷积
给定多项式
\(f(x)=\sum_{i=0}^{n-1}f_ix^i\)
\(g(x)=\sum_{i=0}^{m-1}g_ix^i\)
\(h(x)=f(x)\cdot g(x)=\sum_{i=0}^{n+m-2}x_i\sum_{k=0}^if_kg_{i-k}\)
我们可以知道 \(h(x)\) 的系数
这种形式被称为加法卷积,一般地
形式被称为 \(\circ\) 卷积(\(\circ\) 是某种运算),本篇只探讨加法卷积。
可以发现加法卷积单次复杂度为 \(\mathcal O(n)\),由于要计算每一项系数的加法卷积,故总复杂度为 \(\mathcal O(n^2)\) 不够优秀,考虑从其他方面思考。
点值表示法
上述表达多项式的方法叫做系数表达法,同时多项式可以用 \(n\) 个不同的点唯一确定一个 \(n-1\) 次多项式,这种表达方法叫做点值表达法。
点击查看证明
将 $n$ 个点中的 $x$ 分别带入建立 $F(x)=y$ 的方程,一共 $n$ 个方程。写成系数矩阵和增广矩阵因为各个点都不相同,化简成行阶梯形矩阵可以看到系数矩阵的秩等于增广矩阵的秩,所以该多项式系数存在唯一解。因为 \(f(x)g(x)=h(x)\),所以知道 \(f\) 和 \(g\) 的 \(n+m-1\) 个点,则可以求出 \(h\) 的 \(n+m-1\) 个点,从而唯一确定 \(h\)。所以我们要实现如何从系数表达法到点值表达法以及如何从点值表达法到系数表达法。
\(\texttt{DFT}\)
\(\texttt{DFT}\) 即将系数表达法转化点值表达法。对于多项式 \(F(x)\) 其 \(\deg F=n-1\),我们可以选择带任意 \(n\) 个值从而转化为点值表达法。我们考虑带入自然数,当我们带入 \(x=\pm1\) 时,多项式比较好计算,带入 \(2\) 等其他自然数,计算就比较复杂。我们发现 \((\pm1)^2=1\),很像上文提到的单位根,所以我们考虑带入单位根能否化简计算过程,由于要求 \(n\) 个点值,我们选择 \(n\) 次单位根,其实 \(\texttt{DFT}\) 可以 \(\mathcal O(n\log n)\) 分治求出,为了方便分治,我们将多项式的项数补成一个 \(2\) 的整数次幂,下面请看推导过程:
我们先分离奇偶项
下面我们设
所以有
这样可以将 \(F(x)\) 用 \(F_{\text{even}}(x)\) 与 \(F_{\text{odd}}(x)\) 表达
带入单位根 \(\omega_n^k\)
所以已知 \(F_{\text{even}}(\omega_{n/2}^{k})\) 和 \(F_{\text{odd}}(\omega_{n/2}^{k})\) 可以求 \(F(\omega_n^k)\) 和 \(F(\omega_n^{k+n/2})\),所以 \(F(x)\) 求 \(n\) 次单位根点值可以分治成 \(F_{\text{even}}\) 和 \(F_{\text{odd}}\) 求 \(\dfrac n2\) 次单位根点值。
\(\texttt{IDFT}\)
有了 \(\texttt{DFT}\) 的经验后,不妨用线性代数的视角看待 \(\texttt{DFT&IDFT}\),我们设单位根矩阵
我们设系数向量
我们设点值向量
显然 \(\mathbf y=A\mathbf t\)。
\(\texttt{DFT}\) 实质上就是已知 \(A\) 与 \(\mathbf t\) 求 \(\mathbf y\),\(\texttt{IDFT}\) 实质上就是已知 \(\mathbf y\) 与 \(A\) 求 \(t\),考虑构造 \(A\) 的逆 \(A^{-1}\)。
可以证明
点击查看证明
由矩阵乘法的定义可知 $$ \begin{aligned} (AB)_{ij}&=\sum_{k=1}^{n}A_{ik}\cdot B_{kj}\\ &=\sum_{k=0}^{n-1}(\omega_n^i)^k(\omega_n^{-k})^j\\ &=\sum_{k=0}^{n-1}\omega_n^{k(i-j)}\\ \end{aligned} $$ 由单位根的求和性质显而易见 $\dfrac 1nB$ 即为 $A$ 的逆矩阵。位逆序置换
依据上述可以实现递归版,但是递归版常数较大,经常会被卡常,考虑如何实现非递归实现,下面给出较为通用的实现方法:我们处理出每个 \(i\) 递归计算至最后的位置 \(\text{rev}(i)\)。下面以八次多项式为例说明
| \(\texttt{pos}\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
|---|---|---|---|---|---|---|---|---|
| \(\texttt{Begin}\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(\texttt{bin}\) | \(000\) | \(001\) | \(010\) | \(011\) | \(100\) | \(101\) | \(110\) | \(111\) |
| \(\texttt{End}\) | \(0\) | \(4\) | \(1\) | \(5\) | \(2\) | \(6\) | \(3\) | \(7\) |
| \(\texttt{bin}\) | \(000\) | \(100\) | \(010\) | \(110\) | \(001\) | \(101\) | \(011\) | \(111\) |
我们可以发现 \(\texttt{rev}(i)\) 其实是 \(i\) 的逆序。可以用类似 \(\texttt{DP}\) 的思想 \(\mathcal O(n)\) 递推,递推式为 \(\texttt{rev}(i)=(\texttt{rev}(i>>1)>>1)\or((i\and 1)<<(\log_2n-1))\),其中 \(<<,>>\) 分别表示左移和右移。
求得 \(\texttt{rev}(i)\) 后,我们将第 \(i\) 项的系数交换至 \(\texttt{rev}(i)\)。然后自底向上 \(\texttt{DFT}\),然后将 \(\texttt{DFT)}\) 存放至原来的系数上,每次合并两部分答案。可以发现 \(\texttt{IDFT}\) 相较于 \(\texttt{DFT}\) 只是将 \(\omega_n^k\) 变为 \(\omega_n^{-k}\),最后再除以 \(n\),所以我们可以一个函数实现 \(\texttt{DFT&IDFT}\)。
\(A\) 与 \(B\)进行多项式乘法需要
第一步求出 \(A,B\) 点值表达法并相乘:\(D=\texttt{DFT}(A)\cdot\texttt{DFT}(B)\)
第二步用 \(C\) 的点值表达法 \(D\) 求出 \(C\):\(C=\texttt{IDFT}(D)\)
故时间复杂度为 \(T(n)=2T(\dfrac n2)+\mathcal O(n)=\mathcal O(n\log n)\)。
模板题
直接用 \(\texttt{FFT}\) 即可,注意 \(n,m\) 不是 \(A,B\) 的项数而是其度数。
\(\texttt{Code}\)
点击查看代码
#include<bits/stdc++.h>
#define MOD (1000000007)
#define ll long long
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define lowbit(x) (x&-x)
#define Swap(x,y) (x^=y,y^=x,x^=y)
using namespace std;
void read(ll &x)
{
register char ch=0;register bool f=0;x=0;
while(ch<'0'||ch>'9'){f|=!(ch^'-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
x=f?-x:x;
}
void write(ll x,bool bk)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(!x)
{
if(!bk) putchar('0');
return;
}
write(x/10,1);
putchar((x%10)^48);
}
void print(ll x,char ch)
{
write(x,0);
if(ch) putchar(ch);
}
ll rev[2097157];
const double PI=acos(-1);
struct Complex{
double x,y;
Complex(){}Complex(double nx,double ny):x(nx),y(ny){}
Complex operator+(Complex t){return (Complex){x+t.x,y+t.y};}
Complex operator-(Complex t){return (Complex){x-t.x,y-t.y};}
Complex operator*(Complex t){return (Complex){(x*t.x-y*t.y),x*t.y+y*t.x};}
Complex operator*(double lamdba){return (Complex){x*lamdba,y*lamdba};}
Complex operator/(double lamdba){return (Complex){x/lamdba,y/lamdba};}
}A[2097157],B[2097157];
void FFT(ll n,Complex* Arr,ll flg)
{
for(ll i=0;i<n;i++) if(i<rev[i]) swap(Arr[i],Arr[rev[i]]);
for(ll i=2,step=1;i<=n;i<<=1,step<<=1)
{
Complex w(cos(PI/step),flg*sin(PI/step));
for(ll j=0;j<n;j+=i)
{
Complex r(1,0);
for(ll k=0;k<step;k++,r=r*w)
{
Complex ev(Arr[j+k]),ov(r*Arr[j+k+step]);
Arr[j+k]=ev+ov,Arr[j+k+step]=ev-ov;
}
}
}
if(!~flg) for(ll i=0;i<n;i++) Arr[i]=Arr[i]/n;
}
void Polymul(ll n,ll m,Complex* A,Complex* B,Complex* C)
{
ll len=1,t=0;
static Complex tpA[2097157],tpB[2097157];
for(;len<n+m-1;len<<=1,++t);
for(ll i=0;i<len;i++)
{
//printf("tpA[%lld]=%lf\ntpB[%lld]=%lf\n",i,A[i].x,i,B[i].x);
tpA[i]=A[i],tpB[i]=B[i];
rev[i]=((rev[i>>1]>>1)|((i&1)<<t>>1));
}
FFT(len,tpA,1),FFT(len,tpB,1);
for(ll i=0;i<len;i++)
{
C[i]=tpA[i]*tpB[i];
// printf("tpA[%lld]=(%lf)+(%lf)i\n",i,tpA[i].x,tpA[i].y);
// printf("tpB[%lld]=(%lf)+(%lf)i\n",i,tpB[i].x,tpB[i].y);
}
FFT(len,C,-1);
}
ll n,m;
int main()
{
read(n),read(m);
++n,++m;
for(ll i=0;i<n;i++)
{
ll tp;
read(tp);
A[i].x=tp;
}
for(ll i=0;i<m;i++)
{
ll tp;
read(tp);
B[i].x=tp;
}
Polymul(n,m,A,B,A);
for(ll i=0;i<n+m-1;i++)
print((ll)round(A[i].x),' ');
}
\(\texttt{NTT}\)
\(\texttt{NTT}\)
可以看出,上面 \(\texttt{FFT}\) 涉及了许多浮点数运算,所以精度要求高,系数的值域如果更大则无法接受其精度。而在实际计数时,我们经常需要对一个数取模,所以下面介绍一种在模 \(p\),意义下的替代方案。
我们发现 \(\texttt{FFT}\) 需要浮点数计算的根本原因是 \(\texttt{FFT}\) 分治时依赖单位根,所以我们想找到单位根在模 \(p\) 意义下的替代品,事实说明原根是单位根的替代品,而依赖原根的变换称为 \(\texttt{NTT}\)。
阶
对于数 \(a\),\(a\) 对于 \(p\) 的阶定义为满足 \(a^x\equiv1\pmod p\) 的最小正整数解,记为 \(\delta_p(a)\),在 \(gcd(a,p)\not=1\) 时,阶为 \(\infty\) 或被认为不存在。\(\delta_p(a)\) 的上界从欧拉定理可知为 \(\varphi (p)\)。
原根
当 \(\delta_p(g)=\varphi (p)\) 时,\(g\) 被称为是 \(p\) 的原根。
性质
实现
用原根替换单位根即可,注意取模。
\(\texttt{Code}\)
点击查看代码
#include<bits/stdc++.h>
#define MOD (998244353)
#define ll long long
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define lowbit(x) (x&-x)
#define Swap(x,y) (x^=y,y^=x,x^=y)
using namespace std;
void read(ll &x)
{
register char ch=0;register bool f=0;x=0;
while(ch<'0'||ch>'9'){f|=!(ch^'-');ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
x=f?-x:x;
}
void write(ll x,bool bk)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(!x)
{
if(!bk) putchar('0');
return;
}
write(x/10,1);
putchar((x%10)^48);
}
void print(ll x,char ch)
{
write(x,0);
if(ch) putchar(ch);
}
ll rev[2097157];
const ll g=3;
ll qpow(ll x,ll y)
{
ll res=1;
while(y)
{
if(y&1) res=res*x%MOD;
x=x*x%MOD,y>>=1;
}
return res;
}
// const double PI=acos(-1);
// struct Complex{
// double x,y;
// Complex(){}Complex(double nx,double ny):x(nx),y(ny){}
// Complex operator+(Complex t){return (Complex){x+t.x,y+t.y};}
// Complex operator-(Complex t){return (Complex){x-t.x,y-t.y};}
// Complex operator*(Complex t){return (Complex){(x*t.x-y*t.y),x*t.y+y*t.x};}
// Complex operator*(double lamdba){return (Complex){x*lamdba,y*lamdba};}
// Complex operator/(double lamdba){return (Complex){x/lamdba,y/lamdba};}
// }A[2097157],B[2097157];
ll A[2097157],B[2097157];
void NTT(ll n,ll* Arr,ll flg)
{
for(ll i=0;i<n;i++) if(i<rev[i]) swap(Arr[i],Arr[rev[i]]);
for(ll i=2,step=1;i<=n;i<<=1,step<<=1)
{
ll w=qpow(g,(MOD-1)/i);
if(!~flg) w=qpow(w,MOD-2);
for(ll j=0;j<n;j+=i)
{
ll r=1;
for(ll k=0;k<step;k++,r=r*w%MOD)
{
ll ev=Arr[j+k],ov=r*Arr[j+k+step]%MOD;
Arr[j+k]=(ev+ov)%MOD,Arr[j+k+step]=((ev-ov)%MOD+MOD)%MOD;
}
}
}
if(!~flg)
{
ll inv=qpow(n,MOD-2);
for(ll i=0;i<n;i++) Arr[i]=Arr[i]*inv%MOD;
}
}
void Polymul(ll n,ll m,ll* A,ll* B,ll* C)
{
ll len=1,t=0;
static ll tpA[2097157],tpB[2097157];
for(;len<n+m-1;len<<=1,++t);
for(ll i=0;i<len;i++)
{
//printf("tpA[%lld]=%lf\ntpB[%lld]=%lf\n",i,A[i].x,i,B[i].x);
tpA[i]=A[i],tpB[i]=B[i];
rev[i]=((rev[i>>1]>>1)|((i&1)<<t>>1));
}
NTT(len,tpA,1),NTT(len,tpB,1);
for(ll i=0;i<len;i++)
{
C[i]=tpA[i]*tpB[i];
// printf("tpA[%lld]=(%lf)+(%lf)i\n",i,tpA[i].x,tpA[i].y);
// printf("tpB[%lld]=(%lf)+(%lf)i\n",i,tpB[i].x,tpB[i].y);
}
NTT(len,C,-1);
}
ll n,m;
int main()
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
read(n),read(m);
++n,++m;
for(ll i=0;i<n;i++) read(A[i]);
for(ll i=0;i<m;i++) read(B[i]);
Polymul(n,m,A,B,A);
for(ll i=0;i<n+m-1;i++)
print(A[i],' ');
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号