动态规划之编辑距离问题

问题描述:

 

对于序列S和T, 它们之间的距离定义为: 对二者其一进行几次以下操作: 1, 删除一个字符; 2, 插入一个字符; 3, 改变一个字符. 每进行一次操作, 计数增加1. 将S和T变为相等序列的最小计数就是两者的编辑距离(edit distance)或者叫相似度. 请给出相应算法及其实现. 

 

分析:

 

假设序列S和T的长度分别为m和n, 两者的编辑距离表示为edit[m][n]. 则对序列进行操作时存在以下几种情况:

• a, 当S和T的末尾字符相等时, 对末尾字符不需要进行上述定义操作中(亦即"编辑")的任何一个, 也就是不需要增加计数. 则满足条件: edit[m][n] = edit[m - 1][n - 1].
• b, 当S和T的末尾字符不相等时, 则需要对两者之一的末尾进行编辑, 相应的计数会增加1.
• b1, 对S或T的末尾进行修改, 以使之与T或S相等, 则此时edit[m][n] = edit[m - 1][n - 1] + 1;
• b2, 删除S末尾的元素, 使S与T相等, 则此时edit[m][n] = edit[m - 1][n] + 1;
• b3, 删除T末尾的元素, 使T与S相等, 则此时edit[m][n] = edit[m][n - 1] + 1;
• b4, 在S的末尾添加T的尾元素, 使S和T相等, 则此时S的长度变为m+1, 但是此时S和T的末尾元素已经相等, 只需要比较S的前m个元素与T的前n-1个元素, 所以满足edit[m][n] = edit[m][n - 1] + 1;
• b5, 在T的末尾添加S的尾元素, 使T和S相等, 此时的情况跟b4相同, 满足edit[m][n] = edit[m - 1][n] + 1;
• c, 比较特殊的情况是, 当S为空时, edit[0][n] = n; 而当T为空时, edit[m][0] = m; 这个很好理解, 例如对于序列""和"abc", 则两者的最少操作为3, 即序列""进行3次插入操作, 或者序列"abc"进行3次删除操作.

所以, 以上我们不难推出编辑距离的动态规划方程为:

, 其中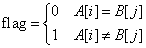

 

所以, 字符串编辑距离的动态规划算法的递归实现可以用如下的Java代码表示:

    public static int editDistance(String a, String b) {
        if (a == null || b == null) {
            return -1;
        }
        return editDistance(a, a.length() - 1, b, b.length() - 1);
    }

    public static int editDistance(String a, int m, String b, int n) {
        if (m < 0 || n < 0) {
            return 1;
        } else if (a.charAt(m) == b.charAt(n)) {
            return editDistance(a, m - 1, b, n - 1);
        } else {
            return Math.min(Math.min(editDistance(a, m - 1, b, n) + 1, editDistance(a, m, b, n - 1) + 1), editDistance(a, m - 1, b, n - 1) + 1);
        }
    }

 

UPDATE:

同时, 由编辑距离的动态规划方程我们可以看出, edit[m][n]可以由edit[m - 1][n - 1], edit[m - 1][n], edit[m][n - 1]得出, 而如果edit是一个二维数组的话, edit[m][n]可以由它的上, 左, 左上三个位置的元素通过条件判断得出. 亦即我们可以通过遍历二维数组, 然后通过回溯来计算当前值.

例如对于字符串S = "sailn"和T = "failing", 对二维数组进行初始化为:

m\n		f	a	i	l	i	n	g
	0	1	2	3	4	5	6	7
s	1	1
a	2
i	3
l	4
n	5

因为S[0] = s, T[0] = f, 则S[0] != T[0], 则对应于上述二维矩阵, edit[1][1] = min(edit[0][0], edit[0][1], edit[1][0]) + 1即edit[1][1] = min(0, 1, 1) + 1即edit[1][1] = 0 + 1 = 1. 

m\n		f	a	i	l	i	n	g
	0	1	2	3	4	5	6	7
s	1	1	2	3	4	5	6	7
a	2	2	1
i	3
l	4
n	5

而对于S[1] = a, T[1] = a, S[1] = T[1], 则对应于二维矩阵, edit[2][2] = edit[1][1], 所以edit[2][2] = 1. 所以按照这种规则, 将上述二维矩阵填满则如下:

m\n		f	a	i	l	i	n	g
	0	1	2	3	4	5	6	7
s	1	1	2	3	4	5	6	7
a	2	2	1	2	3	4	5	6
i	3	3	2	1	2	3	4	5
l	4	4	3	2	1	2	3	4
n	5	5	4	3	2	2	2	3

所以, 两者的编辑距离为edit[m][n] = edit[5][7] = 3.

所以, 按照上述思路即动态规划的回溯解法的Java版本可以如下进行:

    public static int editDistance(String a, String b) {
        if (a == null || b == null) {
            return -1;
        }
        int[][] matrix = new int[a.length() + 1][b.length() + 1];
        for (int i = 0; i < a.length() + 1; i++) {
            for (int j = 0; j < b.length() + 1; j++) {
                if (i == 0) {
                    matrix[i][j] = j;
                } else if (j == 0) {
                    matrix[i][j] = i;
                } else {
                    if (a.charAt(i - 1) == b.charAt(j - 1)) {
                        matrix[i][j] = matrix[i - 1][j - 1];
                    } else {
                        matrix[i][j] = 1 + Math.min(Math.min(matrix[i - 1][j], matrix[i][j - 1]), matrix[i - 1][j - 1]);
                    }
                }
            }
        }
        return matrix[a.length()][b.length()];
    }