大白话解读梯度下降法解决一元线性回归

1.一元线性回归与损失函数

在我们解决一元线性回归进行拟合曲线的时候，常常会使用梯度下降法。

假设我们的数据集为

# 训练数据
x_train = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
y_train = np.array([1, 3, 4, 5, 6, 7, 8, 9, 10])

我们想将其拟合成一条曲线，然后进行训练。拟合曲线表示如下

我们如何去拟合呢？显然两点确定一条直线的。我们就其次，然后求得一个函数，各个点到该函数的方差和最小，于是，我们将其称为损失函数（也叫代价函数、目标函数），该函数如下

该方程为凸函数，并且有极小值。

2.梯度下降法求解最小值

我们解决一个函数的最小值的时候，往往会想到使用导数来求。但是，在多维数据，或者大数据情况下，这种求解方法不适用。

于是，我们有了一个新的方法。

例题：求解y = x^2的极小值

1.我们可以随机取一个点m，假设取到了10， 那么我们显然偏离了，我们进行计算，发现y = 10^2=100，偏右边了怎么办呢？

2.我们将m减去导数，得到100-2*10，靠近了一点点，我们反复取值，即可靠近最低点。

3.在机器学习中，往往允许的误差是极小的，所以，我们应该将m乘上一个alpha值，这个值是学习率，学习率越低，往往拟合函数越好，但是也不是无限低的。

3.梯度下降求解一元线性回归

我们将梯度下降，用来求解一个线性回归，那么任意取值w0, w1

w0, w1每次变动的值为对w0, w1的偏导数，即：

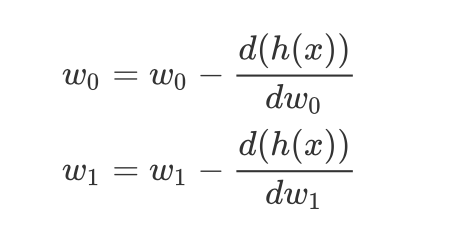
计算可得到：

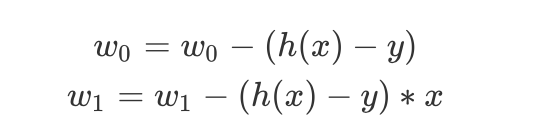
4.由3我们可以得到python代码和拟合图像

import numpy as np
import matplotlib.pyplot as plt

def h(x):
    return w0 + w1 * x // 函数

if __name__ == '__main__':
    # alpha学习率
    rate = 0.02

    # y = w0 * x + w1
    w0 = np.random.normal()
    w1 = np.random.normal()

    # 训练数据
    x_train = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
    y_train = np.array([1, 3, 4, 5, 6, 7, 8, 9, 10])

    err = 1
    # 计算误差函数
    while (err > 0.1):
        for (x, y) in zip(x_train, y_train):
            w0 -= (rate * (h(x) - y) * 1)
            w1 -= (rate * (h(x) - y) * x)

        # 代入找误差
        err = 0.0
        for (x, y) in zip(x_train, y_train):
            err += (y - h(x)) ** 2
        err /= float(x_train.size * 2)

    # 打印
    print("w0的值为%f" % w0)
    print("w1的值为%f" % w1)
    print("误差率的值为%f" % err)

    # 画图
    x = np.linspace(0, 10, 10)
    y = h(x)

    plt.figure()
    plt.plot(x_train, y_train, 'ro')
    plt.plot(x, y)
    plt.title("linear_regression")
    plt.xlabel('x')
    plt.ylabel('h(x)')
    plt.show()

拟合图像如下：

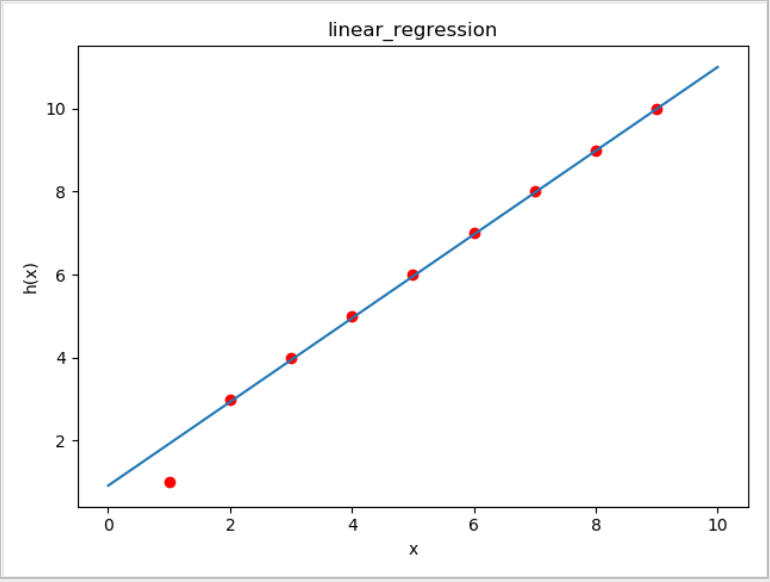
我们发现在编码的过程中，我们有2个停止迭代的条件：

1.尝试次数，尝试次数 < 给定次数（因为有时候你的阈值设置不对会造成死循环）
2.误差值MSE，这个小于误差则拟合成功

5.常见问题

1.如果我们把alpha学习率设置为大于1，那么我们会error，因为，造成了梯度向上

2.如果我们采用绝对值代替方差，可行吗？

不可行，因为平方，会拟合的更完善。而绝对值可能造成过拟合，使我们预测不准确。