数据结构（中）树

一、二叉树

存储：

1.线性存储

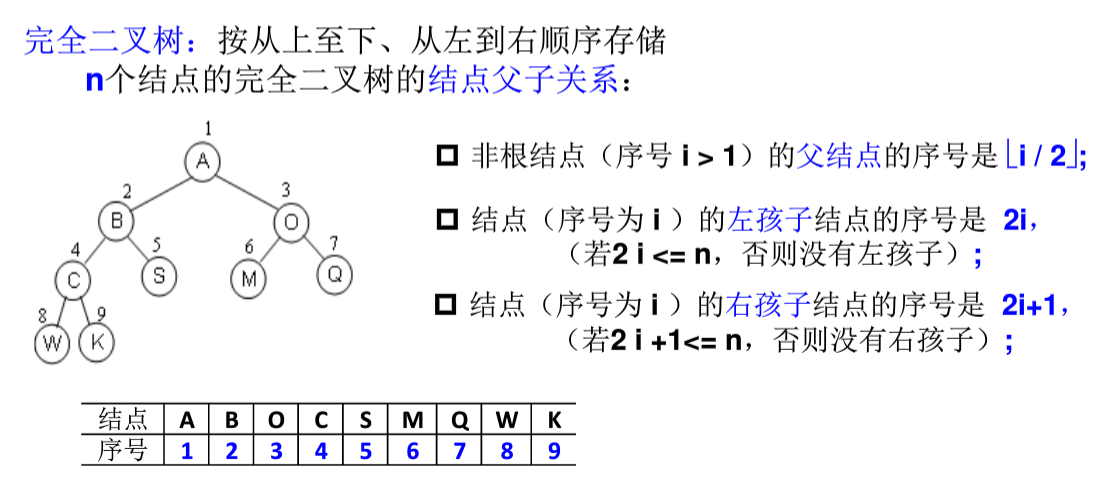
2.链式存储

 

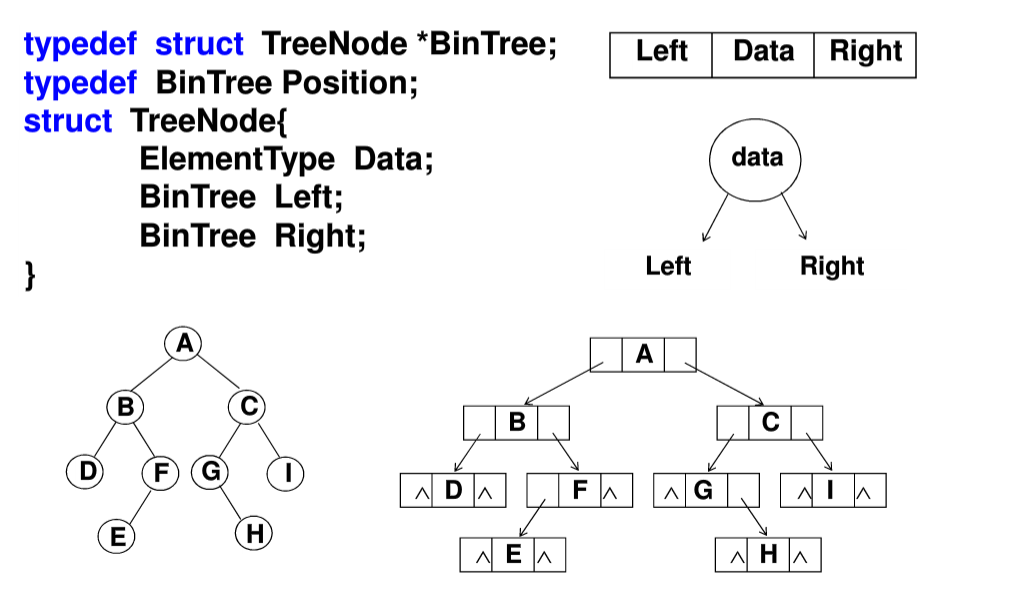
 遍历：

1.先序遍历

2.中序遍历

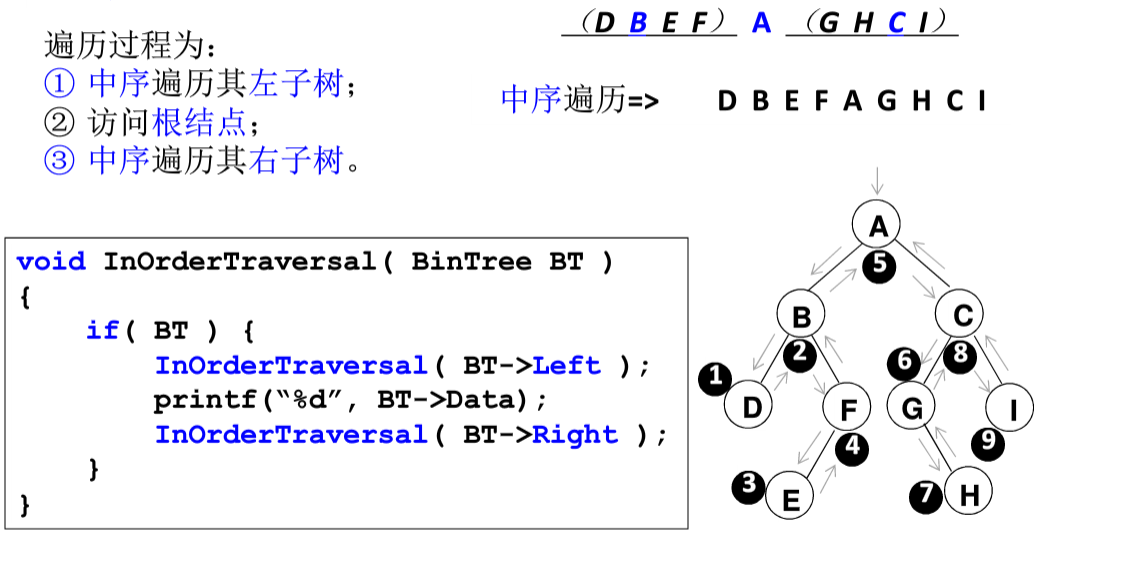
3.后序遍历

 

4.先序遍历堆栈（转自https://blog.csdn.net/weixin_37983220/article/details/84109033 ）

void PreOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = (Stack)malloc(sizeof(SNode));
S->Top = -1;
while (T || !IsEmpty(S))
{
while (T)    //一直向左，并将沿途节点压入堆栈
{
Push(S, T);
printf("%C", T->Data);
T = T->Left;
}
if (!IsEmpty(S))
{
T = Pop(S);
T = T->Right;
}
}
free(S);
}

5.中序遍历堆栈

void InOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = (Stack)malloc(sizeof(SNode));
S->Top = -1;
while (T || !IsEmpty(S))
{
while (T)    //一直向左，并将沿途节点压入堆栈
{
Push(S, T);
T = T->Left;
}
if (!IsEmpty(S))
{
T = Pop(S);
printf("%C", T->Data);
T = T->Right; 
}
}
free(S);
}

6.后序遍历堆栈

void PostOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = (Stack)malloc(sizeof(SNode));

Stack OutPut = (Stack)malloc(sizeof(SNode));
S->Top = -1;
OutPut->Top = -1;
while (T || !IsEmpty(S))
{
while (T)    //一直向左，并将沿途节点压入堆栈
{
Push(S, T);
Push(OutPut, T);
T = T->Right;
}
if (!IsEmpty(S))
{
T = Pop(S);
T = T->Left;
}
}
while (OutPut->Top != -1)
{
printf("%c", Pop(OutPut)->Data);
}
free(S);
free(OutPut);
}

7.层次遍历输出

8.层序遍历输出叶子节点

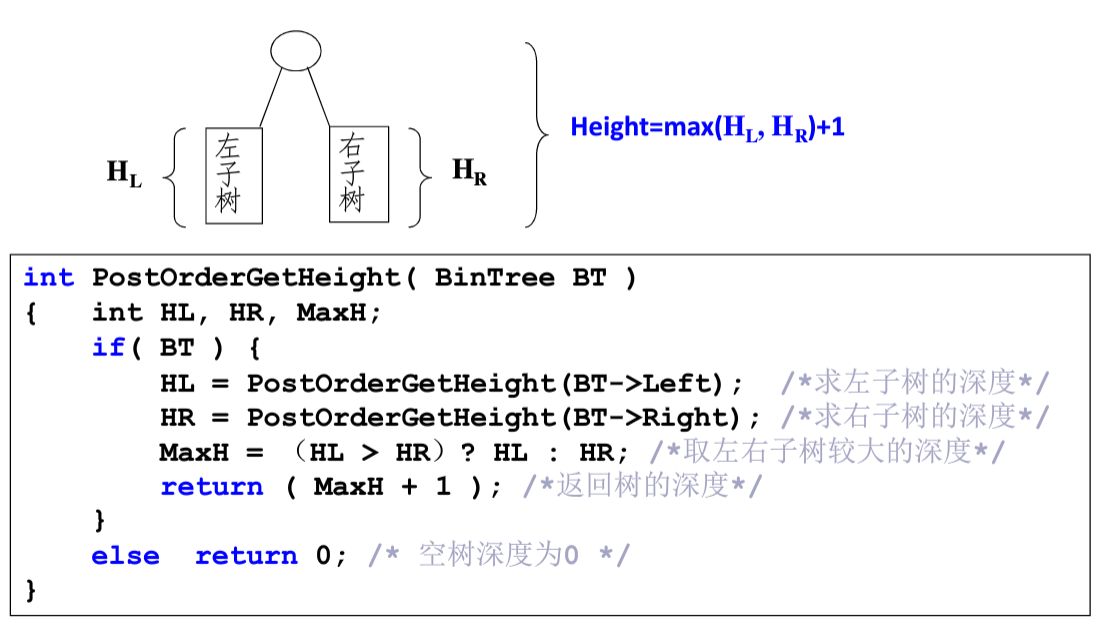
9.二叉树的高度