欧拉图专题
欧拉图专题
一、历史背景
欧拉证明了这种走法是 不可能的。
首先能想到的证明方法是把走七座桥的走法都列出来，一个一个的试验，但七座桥的所有走法共用\(7！=5040种\)，逐一试验将是很大的工作量。欧拉作为数学家，当然没那样想。欧拉把两座岛和河两岸抽象成顶点，每一座桥抽象成连接顶点的一条边，那么哥尼斯堡的七座桥就抽象成下面的图：
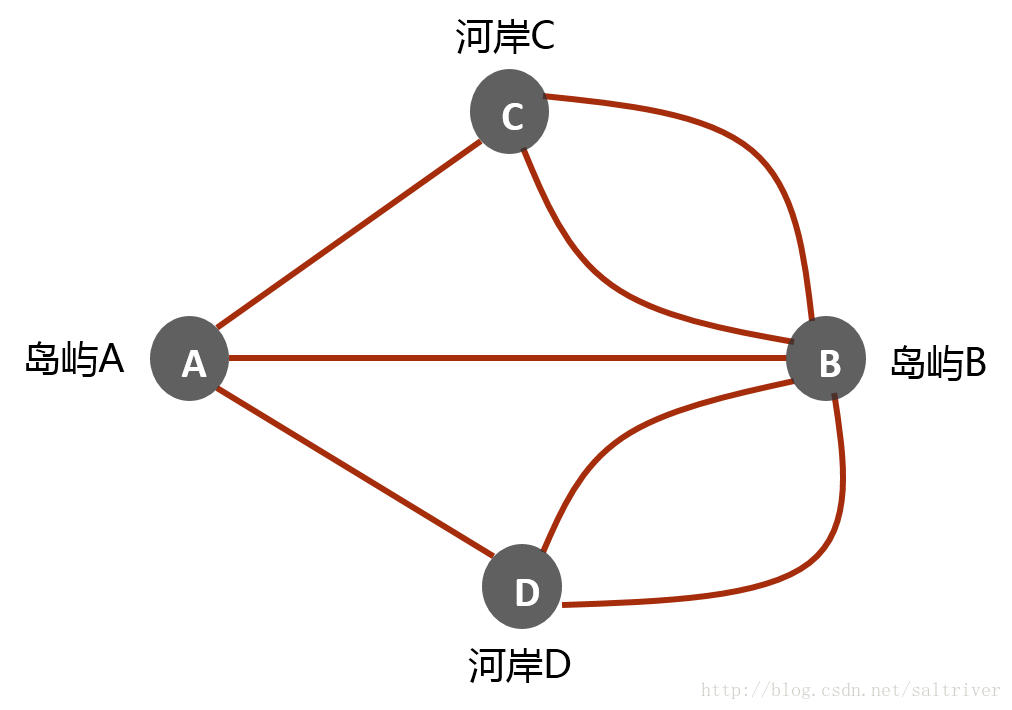
假设每座桥都恰好走过一次，那么对于\(A、B、C、D\)四个顶点中的每一个顶点，需要从某条边进入，同时从另一条边离开。进入和离开顶点的次数是相同的，即每个顶点有多少条进入的边，就有多少条出去的边，也就是说，每个顶点相连的边是成对出现的，即每个顶点的相连边的数量必须是 偶数 。
而上图中\(A、C、D\)四个顶点的相连边都是\(3\)，顶点\(B\)的相连边为\(5\)，都为 奇数。因此，这个图无法从一个顶点出发，遍历每条边各一次。
二、相关的概念和定理
欧拉图、欧拉路径/回路
-
能够不重复地遍历完所有的边的路径——即一笔画的 笔画，称为 欧拉路径
-
如果上述路径的起点与终点相同，则称为 欧拉回路
-
包含欧拉路径的图称为欧拉图
如下\(gif\)所示的图就是欧拉图，存在一个欧拉路径。
下图是一笔画成的 串 字，也就是说烧烤店门口挂的这个字可以用单条\(LED\)灯带做成。
那么柯尼斯堡七桥问题为什么不能 一笔画 呢？来看看欧拉提出的定理:
欧拉定理
欧拉同时考虑到了有向图与无向图的情况，因此要分别讨论。
无向图的情况
定理：
连通无向图\(G\)有欧拉路径的充要条件为：\(G\)中奇度顶点（即与其相连的边数目为奇数的顶点）有\(0\)个或者\(2\)个。
证明：
略
可知，柯尼斯堡七桥问题中的图有\(4个\)奇度顶点（\(1\)个度数为\(5\)，\(3\)个度数为\(3\)），所以不存在欧拉路径。
有向图的情况
定理：
底图连通的有向图\(G\)有欧拉路径的充要条件为：
1、\(G\)的所有顶点入度和出度都相等；
2、或者只有两个顶点的入度和出度不相等，且其中一个顶点的出度与入度之差为\(1\)，另一个顶点的入度与出度之差为\(1\)。
证明:略
欧拉定理介绍完了，那么如何找到具体的路径呢？
寻找欧拉路径/回路
-
① 判断图的连通性,非连通图是不存在欧拉路径/回路的。
判断图的连通性可以通过传统的\(DFS\)方法，也可以通过 并查集 实现，另外还有基于传递闭包的\(Floyd\)-\(Warshall\)算法（没错就是求最短路的那个），可以参考配置习题学习，不再赘述。
图的连通性判断办法
-
② 判断是否存在欧拉路径/回路
如果图是连通的，我们再遍历每个顶点的度（有向图就是入度和出度），根据欧拉定理即可判断图中是否欧拉路径/回路。- 连通 无向图 \(G\)有欧拉路径的充要条件为：\(G\)中奇度顶点（即与其相连的边数目为奇数的顶点）有\(0\)个或者\(2\)个。
- 底图连通的 有向图 \(G\)有欧拉路径的充要条件为：
- \(G\)的所有顶点入度和出度都相等
- 或者只有两个顶点的入度和出度不相等，且其中一个顶点的出度与入度之差为\(1\)，另一个顶点的入度与出度之差为\(1\)
-
③ 找出路径的起点和终点
如果是欧拉路径的话，还能顺便找出路径的起点和终点。
三、题单
\(AcWing\) \(1123\). 铲雪车
【无向图、无需建图、欧拉回路、每一次都可以走不同的路线清雪，不会空车跑】
\(AcWing\) \(1184\). 欧拉回路
【无向图+有向图、稀疏图+链式前向星、找欧拉回路、变态级别的删边优化】
\(AcWing\) \(1124\). 骑马修栅栏
【无向图，稠密图+邻接矩阵、删边优化、记录节点，不是记录边、找欧拉路径起点、字典序=正序枚举+倒序输出】
\(AcWing\) \(1185\). 单词游戏
【有向图，根据入度和出度判断是否符合欧拉通路，再用并查集或\(dfs\)判连通性，\(dfs\)的话，注意删边优化，并查集不需要优化】
\(HDU 1878\) 无向图判定欧拉回路 模板题
【无向图，不用建图，用并查集判连通性,根据入度和出度判断是否符合欧拉通路】
\(POJ\) \(1300\) \(Door\) \(Man\)
【无向图，判断欧拉回路、欧拉路径】
\(P1341\) 无序字母对
【邻接矩阵，无向图，删边，并查集判连通,\(dfs\)求欧拉路径】
\(POJ\) \(1041\) \(John′s\) \(trip\)
【无向图,求边号字典序最小的欧拉回路,需要记录边号，按边号由小到大排序，正序输出；或者按边号由大到小排序，倒序输出,使用结构体进行自定义排序，然后再用链式前向星建图，这一点不如邻接表，邻接表可以直接排序，链式前向星不行，需要结构体辅助】
\(P7771\) 【模板】欧拉路径
【有向图，欧拉路径是否存在，删边，欧拉路径记录，字典序最小】
\(POJ\) \(2337\) \(Catenyms\)
【有向图，欧拉路径是否存在，删边，记录欧拉路径，字典序最小】
\(POJ2230\) \(Watchcow\)
【无向图，欧拉路径】
\(P3520\) [\(POI2011\)]\(SMI\)-\(Garbage\)
【无向图，欧拉回路，多组, \(dfs\)找简单环,欧拉回路拆环】
\(HDU\) - \(5883\) \(The\) \(Best\) \(Path\)
【异或和性质，欧拉通路，欧拉回路，点权与度数的关系】
\(POJ\) \(2513\) \(Colored\) \(Sticks\)
【无向图欧拉路判定，字符串\(HASH\),\(Trie\)树，并查集】
\(HDU\) \(3018\) \(Ant\) \(Trip\)
【需要几笔画完，多个连通分量，奇数度节点个数\(>0\):奇数度节点个数/\(2?1\)】
\(hihoCoder\) \(1182\) 欧拉路·三
【兹鼓欧拉回路】
\(POJ\) \(1392\) \(Ouroboros\) \(Snake\)
【兹鼓欧拉回路,\(2\)进制】
\(POJ\) \(1780\) \(Code\)
【兹鼓欧拉回路,\(10\)进制,循环模拟\(dfs\),手工栈】
\(TODO\) 三轮待刷
\(POJ1637\) \(Sightseeing\) \(tour\)
【网络流，此题已超过目前我的知识范围，暂不学习】
【题 3】CodeForces 36E - Two Paths
【题 4】CodeForces 209C - Trails and Glades
【题 5】洛谷 P5921 - [POI1999] 原始生物
【题 6】CodeForces 547D - Mike and Fish
【题 7】洛谷 P6628 - [省选联考 2020 B 卷] 丁香之路
https://www.cnblogs.com/milmon/p/16586142.html
代码模板
// 记录边的dfs,要注意记录边和记录点的差别
void dfs(int u) {
for (int i = h[u]; ~i; i = h[u]) {
h[u] = ne[i];
dfs(e[i]);
res[++rl] = w[i];
}
}
int getStart() {
int st = 0, a = 0, b = 0, c = 0;
for (int i = 0; i < 26; i++) { // 枚举每个有效节点,每道题的具体实现可能有差异
if (dout[i] != din[i]) a++; // 出度与入度不一致的数量
if (dout[i] == din[i] + 1) b++, st = i; // 起点数量，记录起点
if (dout[i] == din[i] - 1) c++; // 终点数量
}
if (a && (b != 1 || c != 1)) return -1; // 如果有不一致的，并且不是1个，则没有欧拉路径
// 如果是一个环，也是存在欧拉路径的，但所有点的入度和出度一致，st不会被改写，需要再手找出起点。
while (!dout[st]) st++;
return st;
}
