AcWing 2549. 估计人数

\(AcWing\) \(2549\). 估计人数

一、题目

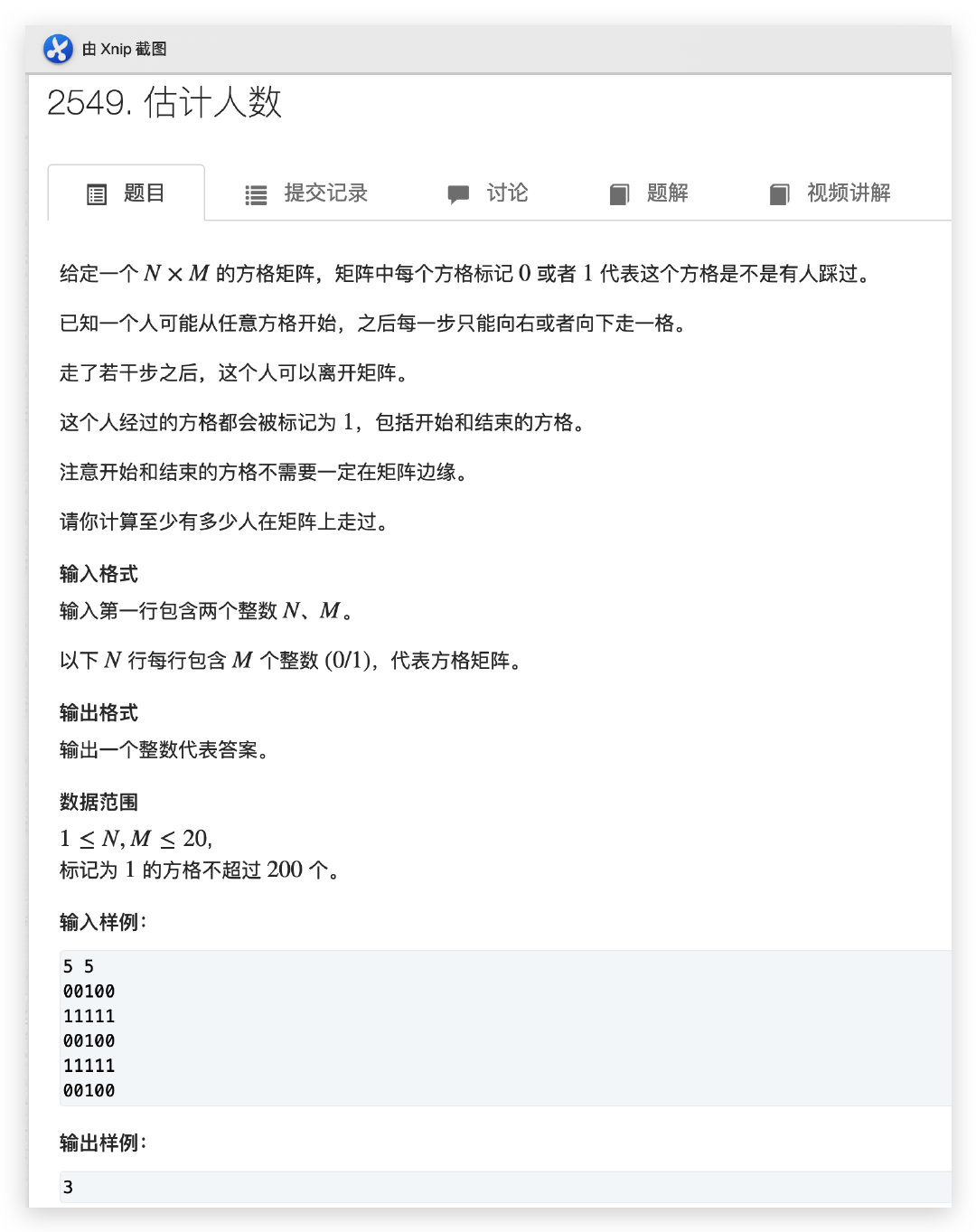
二、题意抽象

• ① 把 可相交的最小路径覆盖 问题转化成 不相交的最小路径覆盖 问题。（可以通过\(floyd\)算法转换）

• ② 求出 不相交的最小路径覆盖 问题的最小路径数（最小路径数=图中节点总数-节点最大匹配度）

• ③ 节点最大匹配度可以通过匈利亚算法求出

三、代码

#include <bits/stdc++.h>
using namespace std;

/*
用最少的人，走完这几条线。最小重复路径点覆盖问题
建图之后，跑一下二分图。
考虑建图：图中‘1’连着完下、或者右走。我们把图中所有的1编号，然后建图，然后floly，然后匈牙利。
*/

const int N = 310;
int n, m; // n行m列的矩阵

int a[N][N], al;
int g[N][N];

// 匈牙利算法
int st[N], match[N];
int dfs(int u) {
    for (int i = 1; i <= n; i++) {
        if (!g[u][i]) continue;           // u->i没有边，不玩了
        if (st[i]) continue;              // i被人预定，我不能选这个妹子
        st[i] = 1;                        // 我选了！
        if (!match[i] || dfs(match[i])) { // 如果以前有人选择了i这个妹子，那么他还有其它选择，那么i让给我
            match[i] = u;
            return 1;
        }
    }
    return 0;
}

int main() {
    cin >> n >> m; // n*m的矩阵

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            char x;
            cin >> x;
            if (x == '1') a[i][j] = ++al; // 每个是1的位置，标识上点的序号
        }

    // 建图
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            if (a[i][j] && a[i][j + 1]) g[a[i][j]][a[i][j + 1]] = 1; // 左右连续1，根据上面的点号建边
            if (a[i][j] && a[i + 1][j]) g[a[i][j]][a[i + 1][j]] = 1; // 上下连续1，根据上面的点号建边
        }

    // 最大点数量
    n = al;

    // Floyd求传送闭包,将传递关系打通,建边
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                g[i][j] |= g[i][k] & g[k][j];

    // 匈牙利算法
    int res = 0;
    for (int i = 1; i <= n; i++) {
        memset(st, 0, sizeof st);
        if (dfs(i)) res++;
    }
    // 最小路径覆盖=节点总数-最大匹配数
    cout << n - res << endl;
    return 0;
}