拓扑排序 专题
拓扑排序专题
拓扑排序指的是有向无环图（\(DAG\)）；
学过计算机网络的知道计算机网络中有一个拓扑结构；
下面就是一个拓扑结构；
那拓扑序就是，图中任意一对顶点\(u\)和\(v\)，若边\(<u,v>∈E(G)\)，则\(u\)在线性序列中出现在\(v\)之前
我们可以发现 拓扑序不是唯一的；
接下来，我们需要知道一个概念——度：
对于有向图的某个结点来说，我们把指向它的边的数量叫做入度；
把从它发出的边的数量称为出度，这个都很好理解吧；
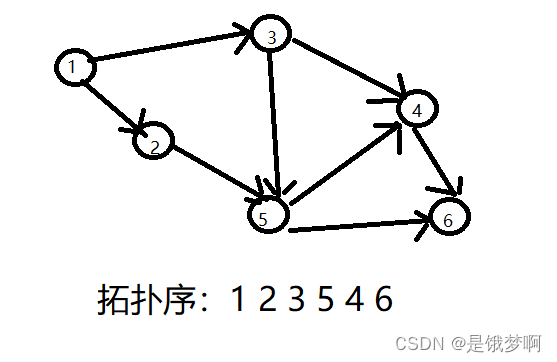
例如，下面这个图：
-
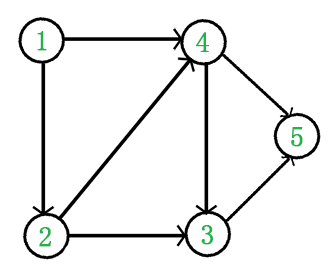
从 \(DAG\) 图中选择一个没有前驱（即入度为\(0\)）的顶点并输出。
-
从图中删除该顶点和所有以它为起点的有向边。
-
重复 \(1\) 和 \(2\) 直到当前的 \(DAG\) 图为空或 当前图中不存在无前驱的顶点为止。
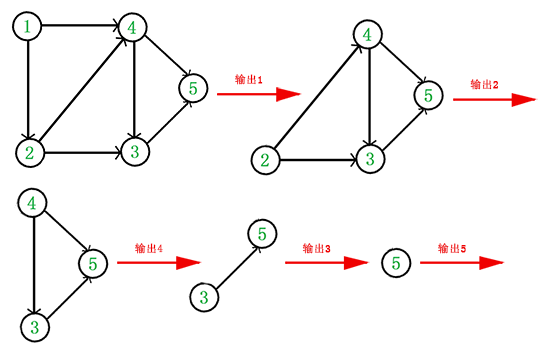
于是，得到拓扑排序后的结果是{ \(1,2,4,3,5\) }。
通常，一个有向无环图可以有一个或多个拓扑排序序列。这是因为可能同时存在多个入度为\(0\)的结点，这时，先处理哪个都是可以的。
如何获得一个拓扑序：
我们先来找一个 最容易理解的例子，那就是食物链，对一个自然界的食物链来说，一定存在拓扑序；
第一：不存在环
第二：有向
接下来我们来看看如何获得一个拓扑序，我们观察最左面的结点，一定是没有指向它的边，也就是入度为零，最右边的结点呢，是一定不存在它指向别人的边的，如果有，那么它就不是最右边的点也就是出度为零；
那就是说，所有入度为零的点都可以作为起点，我们开一个数组记录入度的值；
至于如何使用邻接表存边，这就不展开解释了，可以参考这个：传送门
其实，拓扑排序也是\(bfs\)的一个简单应用，我们需要 借助队列 来实现；
首先，我们遍历存储入度的数组，获得可以作为起点的结点，将其加入队列；
接下来就可以愉快的遍历了，没当我们遍历到一个点的时候，我们让它的入度--；
这样做的 意义 就是，判断指向这个点的边是不是都遍历过了，因为我们要保证拓扑序最重要的一个特点：\(<u,v>\)的边中，\(u\)一定在\(v\)的前面出现；
如果这个点所有的边都遍历过的话，是不是也就是说这个点已经没有指向它的边了，也就是说这个点可以作为一个起点了，那我们将它加入队列；循环这个操作，知道队列为空；
按最小的字典序输出拓扑排序
一个图的拓扑排序往往不只有一种，所以有时题目 要求输出字典序最小的拓扑排序，这时我们只需要把\(bfs\)中的队列 换成优先队列 就好，同时入度为\(0\)的点字典序小的先出队。
题单
\(AcWing\) \(848\). 有向图的拓扑序列
【判断是不是拓扑图的方法，输出任意一个拓扑序列】
\(AcWing\) \(1191\). 家谱树
【输出任意一个拓扑序列】
\(P4017\) 最大食物链计数 - 洛谷
【拓扑序、递推、记录入度的同时记录出度，方便找到终点、数字三角形模型】
\(P1137\) 旅行计划
【拓扑序、递推、记录入度的同时记录出度，方便找到终点、数字三角形模型】
\(AcWing\) \(1192\). 奖金
【拓扑序，给初始值，按拓扑序求最长路，得最小值】
\(AcWing\) \(164\). 可达性统计
【拓扑序，逆拓扑序倒推，\(bitset\)状态压缩,或运算求和】
\(AcWing\) \(456\). 车站分级
【拓扑序，笛卡尔积条边使用中间点降维建图技巧、最长路、最小值】
