AcWing 1322. 取石子游戏
一、状态定义
设 \(L[i][j]\) 表示在 \([i,j]\) 区间的左侧放上一堆数量为 \(L[i][j]\) 的石子后，先手必败。
\(L[i][j]\)可以为\(0\),此时\(a_i \sim a_j\)就已经是必败态了，前面什么也不用加。
| \(L[i][j]\) | \(a_i\) | \(a_{i+1}\) | ... | \(a_{j-1}\) | \(a_{j}\) | \(R[i][j]\) |
|---|
即：\((L[i][j],\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]})\),\((\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]},R[i][j])\) 为 先手必败局面。
二、\(L[i][j]\) 的存在性证明
（\(R[i][j]\) 同理，下同）：
反证法:
假设不存在满足定义的 \(L[i][j]\)，则对于任意非负整数 \(x\)，有形如:
都为必胜局面,记为 \(A(x)\) 局面。
由于 \(A(x)\) 为必胜局面，故从 \(A(x)\) 局面 必然存在\(M\)种一步可达必败局面。
若从最左边一堆中拿，因为假设原因，不可能变成必败局面，因为这样得到的局面仍形如 \(A(x)\)。
注意包括此行在内的接下来几行默认 \(x \neq 0\)
左边拿没用，只能考虑从右边拿：
于是设 \(A(x)\) 一步可达的（某个）必败局面为 \((x,a_i,a_{i+1},\cdots,a_{j-1},y)\)，显然有 \(0 \le y < a_j\)。
由于 \(x\) 有无限个，但 \(y\) 只有 \(a_j\)种——根据抽屉原理，必存在 \(x_1,x_2(x_1 \neq x_2),y\) 满足 \((x_1,a_i,a_{i+1},\cdots,a_{j-1},y)\) 和 \((x_2,a_i,a_{i+1},\cdots,a_{j-1},y)\) 都是必败局面。但这两个必败局面之间实际一步可达，故矛盾，进而原命题成立。
三、\(L[i][j]\) 的唯一性证明
反证法:
假设 \(L(i,j)\) 不唯一，则存在非负整数 \(x_1,x_2(x_1 \neq x_2)\)，使得\((x_1,a_i,a_{i+1},⋯,a_{j−1},a_j)\) 和 \((x_2,a_i,a_{i+1},\cdots,a_{j-1},a_j)\) 均为必败局面。而这两个必败局面之间实际一步可达，故矛盾，进而原命题成立。
四、状态转移
1、边界情况
对于两堆相同的石子，后手进行和先手对称的操作,你咋干我就咋干，我拿完，你瞪眼~
2、场景分析
- 边界情况：\(L[i][i]=a[i]\)
- 变化方法：从左侧拿走一些石子或者从右侧拿走一些石子
- 让我们使用\(L[i][j-1]\)和\(R[i][j-1]\)来表示\(L[i][j]\)和\(R[i][j]\),形成\(DP\)递推关系。
想像一个通用场景:假设现在前面动作都按要求整完了，问我们：本步骤，我们有哪些变化,根据这些变化，怎么样用前面动作积累下来的数据来完成本步骤数据变化的填充。这不就是动态规划吗？
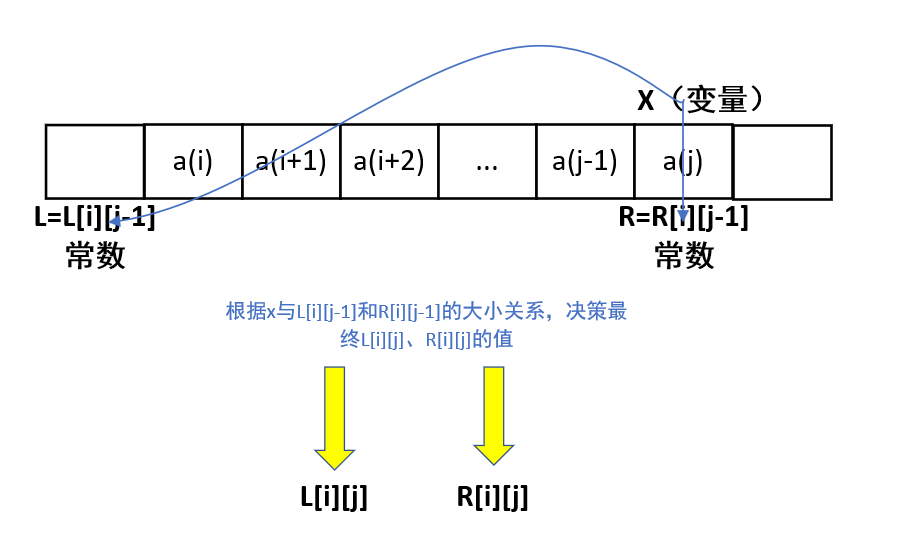
3、推论1
有了上面谁的\(L[i][j]\)唯一性，得出一个有用的推论：
对于任意非负整数 \(x \neq L(i,j)\)，\(\large (x,a_i,a_{i+1},\cdots,a_j)\)为必胜局面。
4、推论2
为方便叙述，下文记 \(L[i][j-1]\) 为 \(L\)，记 \(R[i][j-1]\) 为 \(R\)，并令 \(\displaystyle \large x=a_j(x>0)\)
若 \(R=0\) 则 \(L=R=0\)，此时 \(x>\max\{L,R\}\)，也就是说 \(L=0\) 和 \(R=0\) 都属于 \(Case\) \(5\)，故其它 \(Case\) 满足 \(L,R>0\)。
注：因\(R=0\),表示在[\(i\),\(j-1\)]确定后，右侧为\(0\)就能满足[\(i\),\(j-1\)]这一段为先手必败,此时，左侧增加那堆，个数为\(0\)就可以继续保持原来的先手必败，即\(L=0\)。
4、分类讨论
-
\(x=R\)（\(Case\) \(1\)）
最简单的情况——根据 \(R[i][j-1]\) 的定义，区间 \([i,j]\) 本来就是必败局面，故\[\LARGE L[i][j]=0 \] -
\(x<R\)
- \(x<L\)，即 \(x< \min\{L,R\}\)（\(Case\) \(2\)）
- 结论：
\[\LARGE L[i][j]=x \]-
证明：
即证 \(\large (x,a_i,a_{i+1},\cdots,a_{j-1},x)\)为必败局面。
由于最左边和最右边的两堆石子数量相同，后手可进行和先手对称的操作，后手必将获得一个形如\((y,a_i,a_{i+1},⋯,a_{j−1})\) 或 \((a_i,a_{i+1},\cdots,a_{j-1},y)\) 的局面,其中: \(0<y \le x<\min\{L,R\}\)。
结合 \(L(i,j-1)\) 和 \(R(i,j-1)\) 的定义知这个局面必胜，即后手必胜，先手必败，证毕。
只有左侧为\(L=L(i,j-1)\)这个唯一值时，才是必败态，现在不是\(L=L(i,j-1)\)，而是\(y<min(L,R)\)，所以后手必胜,即先手必败。 -
注意上述证明的前提是 \(x \neq 0\)，因此后续证明若使用 \(Case\) \(2\)，必须满足 \(x \neq 0\)（具体见后文）。
- \(x \geq L\)，即 \(L \leq x < R\)（\(Case\) \(3\)）
-
结论：$$\LARGE L[i][j]=x+1$$
-
证明：
即证 \((x+1,a_i,a_{i+1},\cdots,a_{j-1},x)\)为 必败局面。- 若先手拿最左边一堆，设拿了以后还剩 \(z\) 个石子。
- 若 \(z>L\)，则后手将最右堆拿成 \(z-1\) 个石子（注意 \(z-1 \ge L>0\)），保证左侧比右侧多\(1\)个石子,就能回到 \(Case\) \(3\) 本身，递归证明即可。
- 若 \(z=L\)，则后手将最右堆拿完，根据 \(L[i][j-1]\) 定义知此时局面必败。
- 若 \(0<z<L\)，则后手将最右堆拿成 \(z\) 个石子，由 \(Case\) \(2\) 知此时是必败局面。
- 若 \(z=0\)，此时最右堆石子数 \(k\) 满足 \(L \le k<R\)，结合 \(R[i][j-1]\) 定义知局面必胜。
- 若先手拿最右边一堆，设拿了以后还剩 \(z\) 个石子。
若 \(z \ge L\)，则后手将最左堆拿成 \(z+1\)个石子，递归证明即可。
若 \(0<z<L\)，则后手将最左堆拿成 \(z\) 个石子，由 \(Case\) \(2\) 知此时是必败局面。
若 \(z=0\)，则后手将最左堆拿成 \(L\) 个石子，由 \(L[i][j-1]\)定义知此时局面必败。
- 若先手拿最左边一堆，设拿了以后还剩 \(z\) 个石子。
-
- \(x<L\)，即 \(x< \min\{L,R\}\)（\(Case\) \(2\)）
- \(x>R\)
-
\(x≤L\)，即 \(R < x \leq L\)（\(Case\) \(4\)）
-
结论：$$\LARGE L[i][j]=x-1$$
-
证明：
- 若先手拿最左边一堆，设拿了以后还剩 \(z\) 个石子。
- 若 \(z \geq R\)，则后手将最右堆拿成 \(z+1\) 个石子，保证左侧比右侧多\(1\)个石子,就能回到 \(Case\) \(4\) 本身，递归证明即可。
- 若 \(0<z<R\)，则后手将最右堆拿成 \(z\) 个石子，由 \(Case\) \(2\) 知此时是必败局面。
- 若 \(z=0\)，则后手将最右堆拿成 \(R\) 个石子（注意 \(Case\) \(4\) 保证了此时最右堆石子个数 \(>R\)），由 \(R[i][j-1])\) 的定义知此时是必败局面。
- 若先手拿最右边一堆，设拿了以后还剩 \(z\) 个石子。
- 若 \(z>R\)，则后手将最左边一堆拿成 \(z-1\) 个石子（注意 \(z-1 \ge R >0\)），递归证明即可。保证右侧比左侧多\(1\)个石子。
- 若 \(z=R\)，则后手把最左堆拿完，根据 \(R[i][j-1]\)的定义可知得到了必败局面。
- 若 \(0<z<R\)，则后手将最左堆拿成 \(z\) 个石子，由 \(Case\) \(2\) 知此时是必败局面。
- 若 \(z=0\)，此时最左堆石子数量 \(k\) 满足 \(0<k<L\)，结合 \(L[i][j-1]\) 定义知局面必胜。
- 若先手拿最左边一堆，设拿了以后还剩 \(z\) 个石子。
-
-
\(x>L\)，即 \(x>\max\{L,R\}\)（\(Case\) \(5\)）
-
结论：$$\LARGE L[i][j]=x$$
-
证明：
设先手将其中一堆拿成了 \(z\) 个石子。-
若 \(z>\max\{L,R\}\)，后手将另一堆也拿成\(z\)个，回到 \(Case\) \(5\)，递归证明。
-
若 \(0<z<\min\{L,R\}\)，后手把另一堆也拿成 \(z\) 个石子即可转 \(Case\) \(2\)。
-
若 \(z=0\)，将另一堆拿成 \(L\) 或 \(R\) 个石子即可得到必败局面。
-
剩余的情况是 \(L \le z \le R\)或 \(R \le z \le L\)。
\(Case\) \(3\) 可以解决最左堆 \(L +1 \le z \le R\)，最右堆 \(L \le z \le R-1\) 的情况
\(Case\) \(4\) 可以解决最左堆 \(R \le z \le L-1\)，最右堆 \(R+1 \le z \le L\)的情
况。
所以只需解决最左堆 \(z=L\) 和最右堆 \(z=R\) 的情况。而这两种情况直接把另一堆拿完就可以得到必败局面。
-
-
-
综上所述：
温馨提示：请看清楚 \(L\) 取不取等，乱取等是错的！
同理可求 \(R(i,j)\)。
回到原题，先手必败当且仅当 \(L[2][n]=a_1\) ，于是我们就做完啦！
时间复杂度 \(O(n^2)\)。
五、实现代码
#include <cstdio>
using namespace std;
const int N = 1010;
int n;
int a[N], l[N][N], r[N][N];
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int len = 1; len <= n; len++)
for (int i = 1; i + len - 1 <= n; i++) {
int j = i + len - 1;
if (len == 1)
l[i][j] = r[i][j] = a[i];
else {
int L = l[i][j - 1], R = r[i][j - 1], x = a[j];
if (R == x)
l[i][j] = 0;
else if (x < L && x < R || x > L && x > R)
l[i][j] = x;
else if (L > R)
l[i][j] = x - 1;
else
l[i][j] = x + 1;
// 与上述情况对称的四种情况
L = l[i + 1][j], R = r[i + 1][j], x = a[i];
if (L == x)
r[i][j] = 0;
else if (x < L && x < R || x > L && x > R)
r[i][j] = x;
else if (R > L)
r[i][j] = x - 1;
else
r[i][j] = x + 1;
}
}
if (n == 1)
puts("1");
else
printf("%d\n", l[2][n] != a[1]);
}
return 0;
}
