AcWing 1273. 天才的记忆
. 天才的记忆
一、题目描述
从前有个人名叫 ,他有着天才般的记忆力,他珍藏了许多许多的宝藏。
在他离世之后留给后人一个难题(专门考验记忆力的啊!),如果谁能轻松回答出这个问题,便可以继承他的宝藏。
题目是这样的:给你一大串数字(编号为 到 ,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 个询问,每次询问就给你两个数字 ,要求你瞬间就说出属于 到 这段区间内的最大数。
一天,一位美丽的姐姐从天上飞过,看到这个问题,感到很有意思(主要是据说那个宝藏里面藏着一种美容水,喝了可以让这美丽的姐姐更加迷人),于是她就竭尽全力想解决这个问题。
但是,她每次都以失败告终,因为这数字的个数是在太多了!
于是她请天才的你帮他解决。如果你帮她解决了这个问题,可是会得到很多甜头的哦!
输入格式
第一行一个整数 表示数字的个数。
接下来一行为 个数,表示数字序列。
第三行读入一个 ,表示你看完那串数后需要被提问的次数。
接下来 行,每行都有两个整数 。
输出格式
输出共 行,每行输出一个数,表示对一个问题的回答。
数据范围
。
输入样例:
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3
输出样例:
34
123
123
8
二、问题
询问某个区间内的最大或最小值,一般采用算法,也称表、跳表。
缺陷:离线算法,不能修改,否则需要用到线段树
暴力解法
容易想到的是遍历,查询一次的复杂度是。但当数据量非常大且查询很频繁时,该算法无法在有效的时间内查询出正解,多次时的复杂度是
算法
1、预处理
状态表示
设是要求区间最值的数列,表示 从第个数起连续个数中的最大值
举栗子:
数列为:
表示第个数起,长度为的最大值,其实就是这个数。
;
初始值
可以容易的看出就等于。(的初始值)
状态转移
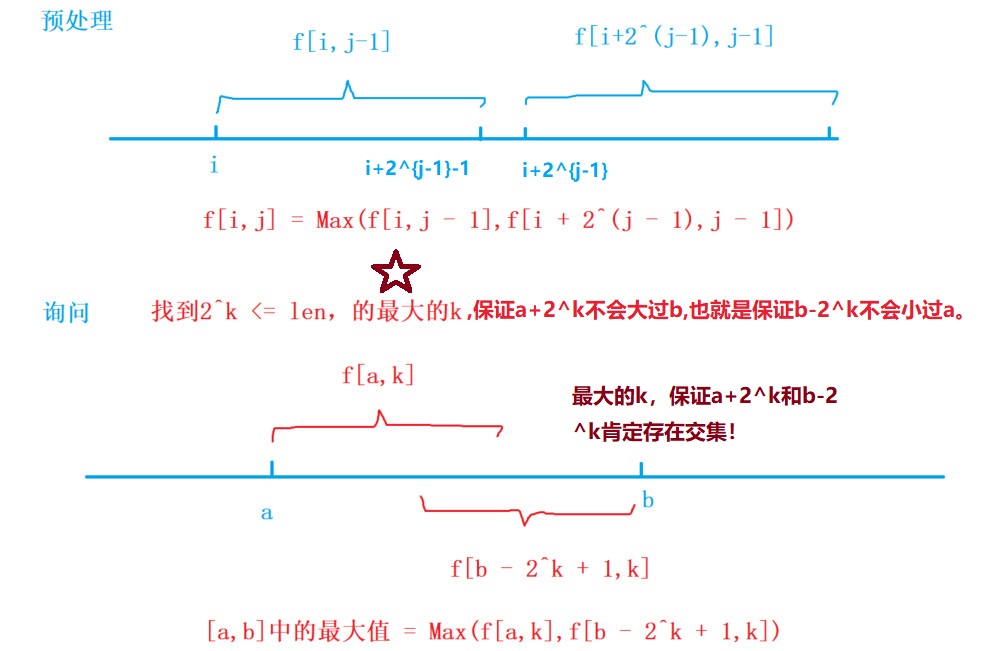
:为什么是外循环而是内循环?
能不能 调换一下嘞?
答案是 不可以,这个类似于 区间,需要先枚举长度。
你可以这样来理解:动态规划体现在二维数组形式上,就是一个二维填表的过程,可能采用的顺序是:
- 从左到右,从上到下去填写
- 从上到下,从左到右去填写
- 从右下角向左上角去填写
- ....
具体该怎么填写,其实是和实际场景相关的,必须 保证无后效性,就是这块填写完了就是填写完了,不能一会用到时说还没有填写,那就彼此依赖不上了。本题如果按列填写,就是依赖于,也就是按列,可以完成任务。如果是按行,你会发现是东一下,西一下,跳来跳去,整不好就在下一个要用到前序数字时,它还没有完成填充,这样彼此就无法实现依赖了!因此需要先枚举,再枚举。
查询
如何确定呢?
对于每个查询 ,需要先找出最大的一个满足 的 ,其中
,方法就是两边求对数:
要想取最大的整数,就是
如果是给整数赋值,就不用写强制转换,故直接写成:
int k = log2(len);
构造交集
查询时通过构建的方法,造成与存在一个交集,分别求与,然后取一个就是答案,虽然这里有一部分是重复的,但求最大值不怕重复!同时,也因为这个原因,使得算法,也就只能用来计算最大最小值,不能用来处理其它需求。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, M = 18;
int n, m;
int w[N];
int f[N][M];
// 预处理
void rmq() {
for (int j = 0; j < M; j++) // 注意是j在外层,类似于区间DP,长度在外层
for (int i = 1; i + (1 << j) - 1 <= n; i++) // i(行)在内层
if (j == 0) // base case 边界值
f[i][j] = w[i];
else
f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
// 查询区间最大值
int query(int l, int r) {
int len = r - l + 1;
int k = log2(len);
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
int main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> w[i];
rmq(); // ST表初始化
cin >> m;
while (m--) {
int l, r;
cin >> l >> r;
printf("%d\n", query(l, r));
}
return 0;
}
四、练习题
最大、最小一起来

思路
这一题是需要用到最大值和最小值两个,求出来后再相减就是答案。
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, M = 20;
int w[N]; // 原始数组
int f[N][M], g[N][M]; // 最大值结果数组,最小值结果数组
int n, q;
/*
输入样例:
6 3
1 7 3 4 2 5
1 5
4 6
2 2
答案:
6
3
0
*/
// 预处理最大值
void rmqMax() {
for (int j = 0; j < M; j++) // 注意是j在外层,类似于区间DP,长度在外层
for (int i = 1; i + (1 << j) - 1 <= n; i++) // i(行)在内层
if (j == 0) // base case 边界值
f[i][j] = w[i];
else
f[i][j] = max(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
// 查询区间最大值
int queryMax(int l, int r) {
int len = r - l + 1;
int k = log2(len);
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
// 预处理最小值
void rmqMin() {
for (int j = 0; j < M; j++) // 注意是j在外层,类似于区间DP,长度在外层
for (int i = 1; i + (1 << j) - 1 <= n; i++) // i(行)在内层
if (j == 0) // base case 边界值
g[i][j] = w[i];
else
g[i][j] = min(g[i][j - 1], g[i + (1 << j - 1)][j - 1]);
}
// 查询区间最小值
int queryMin(int l, int r) {
int len = r - l + 1;
int k = log2(len);
return min(g[l][k], g[r - (1 << k) + 1][k]);
}
int main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> w[i];
rmqMax(); // ST表初始化
rmqMin(); // ST表初始化
while (q--) {
int l, r;
cin >> l >> r;
printf("%d\n", queryMax(l, r) - queryMin(l, r));
}
return 0;
}
最大公约数

这一题跟上一题差不多,只需将改成就行了。
#include <bits/stdc++.h>
using namespace std;
const int N = 200010, M = 18;
/*
输入样例:
5 3
4 12 3 6 7
1 3
2 3
5 5
答案:
1
3
7
*/
int n, q;
int w[N];
int f[N][M];
// 预处理
void rmq() {
for (int j = 0; j < M; j++) // 注意是j在外层,类似于区间DP,长度在外层
for (int i = 1; i + (1 << j) - 1 <= n; i++) // i(行)在内层
if (j == 0) // base case 边界值
f[i][j] = w[i];
else
f[i][j] = __gcd(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
// 查询区间最大值
int query(int l, int r) {
int len = r - l + 1;
int k = log2(len);
return __gcd(f[l][k], f[r - (1 << k) + 1][k]);
}
int main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> q;
for (int i = 1; i <= n; i++) cin >> w[i];
rmq();
while (q--) {
int l, r;
cin >> l >> r;
printf("%d\n", query(l, r));
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享4款.NET开源、免费、实用的商城系统
· 全程不用写代码,我用AI程序员写了一个飞机大战
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了
· 上周热点回顾(2.24-3.2)
2021-07-04 数组初始化方法总结
2017-07-04 360开源的pika