AcWing 1310. 数三角形

题目传送门

引理一

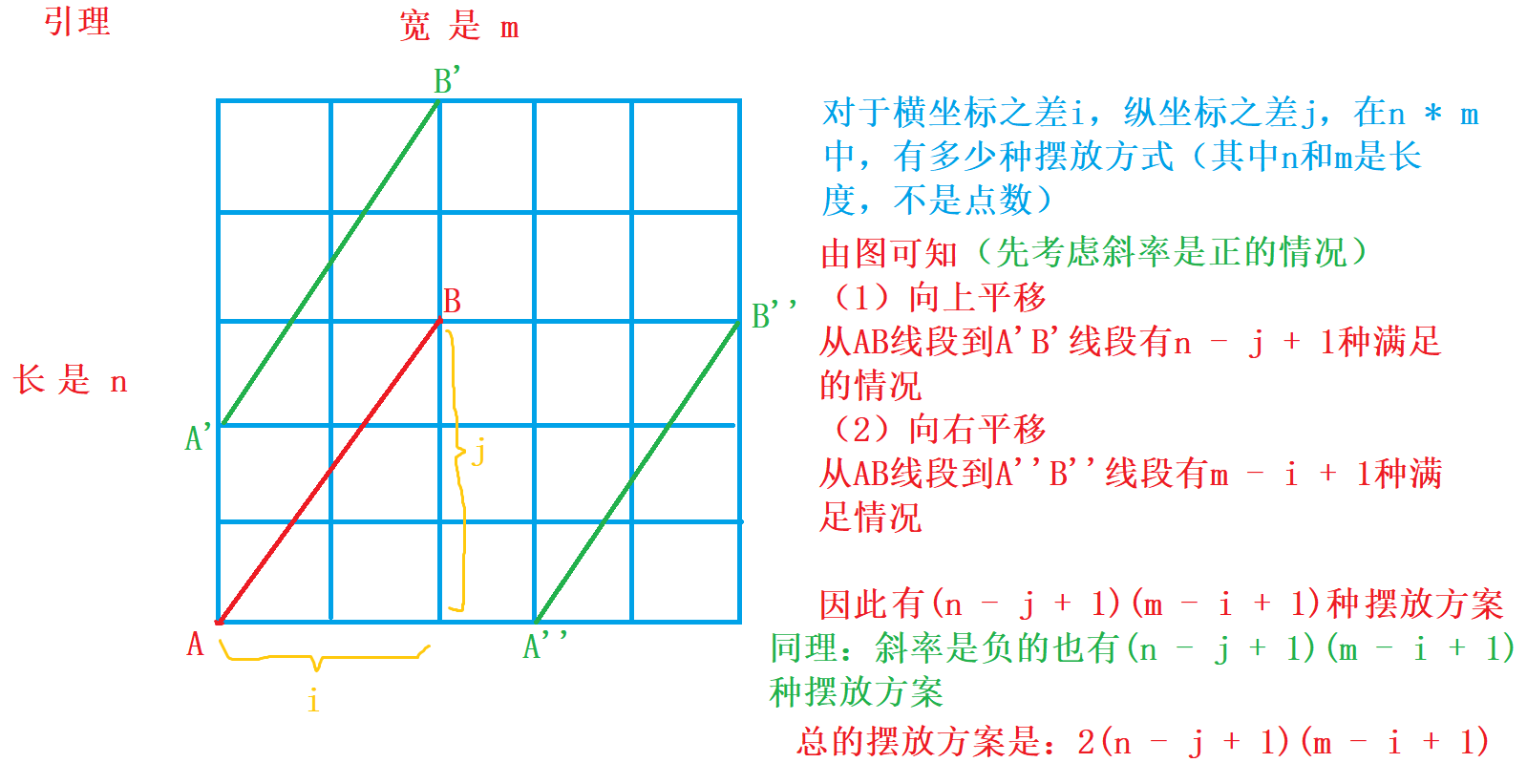
引理二

$gcd(i,j)−1$的证明

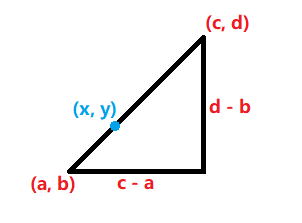
对于斜边上的任何一点 $(x,y)$, 其满足：

$$\large \frac{y-b}{x-a}=\frac{d-b}{c-a}$$

注意：$a≤x≤c,b≤y≤d$

可知：$$\large \displaystyle y=\frac{d-b}{c-a}(x-a)+b=\frac{\frac{d-b}{gcd(d-b,c-a)}}{\frac{c-a}{gcd(d-b,c-a)}}(x-a)+b
\
\Rightarrow
\
y=\frac{d-b}{gcd(d-b,c-a)}*\frac{x-a}{\frac{c-a}{gcd(d-b,c-a)}}+b \ \ \ x \in Z^+

$$那么如果使得 $y∈Z^+$ 的话,必须使得 $\large \displaystyle \frac{c-a}{gcd(d-b,c-a)}|(x-a)$，即： $$\large x=\frac{c-a}{gcd(d-b,c-a)}*q+a$$

对于条件 $b≤y≤d$ 上述式子是由直线方程推出的，因此其在方程中等价于 $a≤x≤c$, 因此我们只需要考虑 $x$ 的范围限制即可:

$$\large a≤x=\frac{c-n}{gcd(d-b,c-a)}*q+a≤c \\ \Rightarrow 0 ≤ q ≤ gcd(d-b,c-a)$$

$q$ 可以取这个区间中的所有整数，因此数量为 $gcd(d−b,c−a)+1$

然后我们分析对于区间中的任意一个点 $(x,y)$, 由于上面 $q$ 的范围可知 $a≤x≤c$, 因此均在斜边上不加上两个端点的话，就是 $gcd(d−b,c−a)−1$

算法分析

本题使用 容斥原理 的思想

题目给定长是$n$，宽是$m$的矩形，因此总端点数有$(n + 1) * (m + 1)$个，从总端点数选$3$个点的情况有
$\large \displaystyle C_{(n+1)∗(m+1)}^3$种，再将不符合三角形规则的情况减去即可，即 三角形的数目 = $\large \displaystyle C_{(n+1)∗(m+1)}^3$- 不满足要求的情况（三点共线）

不满足的情况

• 1、 斜率不存在：$(m+1)C_{n+1}^3$
• 2、 斜率为$0$：$(n+1)C_{m+1}^3$
• 3、斜率存在且不为 $0$：由两个端点 $A，B$ 组成的横坐标之差是 $i$ ，纵坐标之差是 $j$ 的线段共有 $2(n−j+1)(m−i+1)$ 条，对于每一条线段斜率上共有 $gcd(i,j)+1$ 个端点，减去 $A，B$ 两个端点，即第三个点有 $gcd(i,j)−1$ 种满足情况，因此总方案数是 $2(gcd(i,j)−1)(n−j+1)(m−i+1)$