AcWing 1305. GT考试
\(AcWing\) \(1305\). \(GT\)考试
一、题目描述
阿申准备报名参加 \(GT\) 考试，准考证号为 \(n\) 位数 \(X_1X_2⋯X_n\)，他不希望准考证号上出现不吉利的数字。
他的不吉利数字 \(A_1A_2⋯A_m\) 有 \(m\) 位，不出现是指 \(X_1X_2⋯X_n\) 中没有恰好一段等于 \(A_1A_2⋯A_m\)，\(A_1\) 和 \(X_1\) 可以为 \(0\)。
输入格式
第一行输入 \(n,m,K\)。
接下来一行输入 \(m\) 位的不吉利数字。
输出格式
阿申想知道不出现不吉利数字的号码有多少种，输出模 \(K\) 取余的结果。
数据范围
\(0≤X_i,A_i≤9,1≤n≤10^9,1≤m≤20,2≤K≤1000\)
输入样例：
4 3 100
111
输出样例：
81
二、知识图谱
-
扩展方式\(1\)：数据量扩展
\(AcWing\) \(1052\). 设计密码中的\(n\)值最大为\(50\)，本题的\(n\)最大可以取到\(10^9\)。 -
扩展方式\(2\): 不能包含多个字符串
对应题目是：\(AcWing\) \(1053\). 修复\(DNA\)，可以使用\(AC\)自动机解决。
三、暴力\(dp\)
利用\(kmp\)算法求方案数
-
状态表示
设\(f[i][j]\)表示\(dp\)到长串的第\(i\)位，匹配了短串的前缀长度为\(j\)时的 总方案数答案: \(\displaystyle \sum_{j=0}^{m-1}f[n][j]\)
-
状态转移
枚举\(0 \sim 9\)的每一个数，看在匹配 不能出现的串 \(j\)位后 再加当前枚举的数能变成匹配几位，如果匹配\(m\)位了则不合法:- 如果新加的这一位 可以 与 不能出现的串 的下一位匹配，那么就可以转移到 \(f[i + 1][j + 1]\)。
- 如果新加的这一位 不能 与 不能出现的串 的下一位匹配，就往回找第一个能匹配的位置，利用\(kmp\)的\(ne\)数组往回跳，匹配一个新的前缀。假设找到的位置\(u=ne[u]+1\),那么当前状态就可以转移到\(f[i+1][u]\)。
\(40\)分代码
复杂度\(O(nm^2)\)直接爆炸
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, m, mod;
const int N = 1e6 + 10;
int ne[N]; // kmp的ne数组，针对模式串s
char s[N]; // 模式串s
int f[N][22]; // dp数组
//原始版本，就是设计密码那道题的代码，可以过4个点，剩余6个点TLE
int main() {
cin >> n >> m >> mod;
cin >> s + 1;
// kmp
for (int i = 2, j = 0; i <= m; i++) {
while (j && s[j + 1] != s[i]) j = ne[j];
if (s[j + 1] == s[i]) j++;
ne[i] = j;
}
//普通dp
f[0][0] = 1;
for (int k = 0; k < n; k++)
for (int i = 0; i < m; i++)
for (char c = '0'; c <= '9'; c++) {
int j = i;
while (j && s[j + 1] != c) j = ne[j];
if (s[j + 1] == c) j++;
//在kmp过程中进行判断,不能命中m个长度，需要避让
if (j < m) f[k + 1][j] = (f[k + 1][j] + f[k][i]) % mod;
}
int res = 0;
for (int i = 0; i < m; i++) res = (res + f[n][i]) % mod;
printf("%d\n", res);
return 0;
}
四、矩阵优化
时间复杂度\(O(m^3logn)\)
设计密码那道题的\(n<=20\),这道题的数据范围有\(1e9\)!
看到这个另人发指的数量级，感觉到普通\(dp\)肯定凉凉，一定要用特殊手段！
通过上面的分析，我们根据状态计算可以得到第\(i\)层和第\(i+1\)层之间的关系，即
\(\large \left\{\begin{array}{ll} f[i+1][0]=f[i][0] * a[0][0] + f[i][1] * a[1][0]+...+f[i][m-1] * a[m-1][0] & \\ f[i+1][1]=f[i][0] * a[0][1] + f[i][1] * a[1][1]+...+f[i][m-1] * a[m-1][1] & \\ ... & \\ f[i+1][m-1]=f[i][0] * a[0][m-1] + f[i][1] * a[1][m-1]+...+f[i][m-1] * a[m-1][m-1] \end{array}\right. \)
看着像矩阵，构造一下，令： $$\large F[i+1]=(f[i+1][0],f[i+1][1],...,f[i+1][m-1])$$
递推式：
证明：
结论：具有递推性质！
\(Q1:A\)矩阵实际含义
答：\(A[k][j]\) 表示在 和短串匹配长度为\(k\)的串(后缀) 后面添加一个字符，使新构成的串 和短串匹配长度为\(j\)(前缀)，这样的字符添加方案数。
\(Q2:\)\(A\)矩阵求法
答：根据上面的分析可知，矩阵\(A\)只与不合法串\(S\)有关，因此\(A\)矩阵是不变的。根据上面递推式可知：
如何求解数组\(A\)呢？如果从\(f(i, j)\)可以转移到\(f(i+1, k)\)，则让\(a[j, k]++\)。即让\(f(i+1, k) += f(i, j)\)：
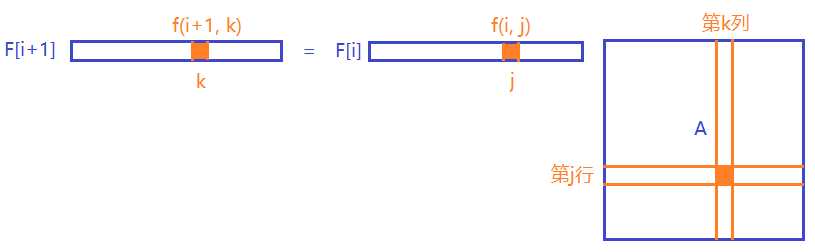
求出向量\(F(n)\)后，最后的答案就是向量\(F(n)\)中所有的元素之和。
总结
对于所有类似于本题的\(DP\)问题(状态转移方程是线性的)都可以采用快速幂的优化方式
\(AC\)代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 25;
int n, m, mod;
char s[N];
int ne[N];
int a[N][N];
//矩阵乘法
void mul(int a[][N], int b[][N], int c[][N]) {
int t[N][N] = {0};
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
for (int k = 0; k < N; k++)
t[i][j] = (t[i][j] + (LL)(a[i][k] * b[k][j]) % mod) % mod;
}
memcpy(c, t, sizeof t);
}
int main() {
cin >> n >> m >> mod;
cin >> s + 1;
// kmp
for (int i = 2, j = 0; i <= m; i++) {
while (j && s[j + 1] != s[i]) j = ne[j];
if (s[j + 1] == s[i]) j++;
ne[i] = j;
}
// 初始化A[i][j]
for (int i = 0; i < m; i++)
for (int c = '0'; c <= '9'; c++) {
int j = i;
while (j && s[j + 1] != c) j = ne[j];
if (s[j + 1] == c) j++;
if (j < m) a[i][j]++;
}
// f[0][0]=1 base case
int f[N][N] = {1};
//矩阵快速幂
for (int i = n; i; i >>= 1) {
if (i & 1) mul(f, a, f); // f:基底 a:需要计算快速幂的常数矩阵 f:结果存储
mul(a, a, a); //倍增a
}
int res = 0;
for (int i = 0; i < m; i++) res = (res + f[0][i]) % mod;
printf("%d\n", res);
return 0;
}
