AcWing 220. 最大公约数
\(AcWing\) \(220\). 最大公约数
一、题目描述
给定整数 \(N\)，求 \(1≤x,y≤N\) 且 \(GCD(x,y)\) 为素数的 数对\((x,y)\) 有多少对。
\(GCD(x,y)\) 即求 \(x，y\) 的最大公约数。
输入格式
输入一个整数 \(N\)。
输出格式
输出一个整数，表示满足条件的数对数量。
数据范围
\(1≤N≤10^7\)
输入样例：
4
输出样例：
4
二、解题思路
最开始读错题，成了: \(1<=x,y<=N\),并且\(gcd(x,y)=1\)有多少数对？
这不就是在计算\(\displaystyle \sum_{i=1}^{N}φ(i)\)吗？
其实本题不是说\(gcd(x,y)=1\)，而是说\(gcd(x,y)=p\),其中\(p\)是质数 。
1、解读样例
先来看一下样例：\(n=4\)时，答案是\(4\)。
手动枚举一下：
\(gcd(2,2)=2\),\(gcd(3,3)=3\),\(gcd(2,4)=2\),\(gcd(4,2)=2\)
就这四个，因为只有这几种组合，最大公约数才是质数,组数是\(4\)组。
\(gcd(2,3)=1,gcd(3,2)=1,gcd(3,4)=1,gcd(4,3)=1\)，结果不是质数而是\(1\)，不符合要求。
可以看得出来，由这个样例推出：这里\(gcd(2,4)=gcd(4,2)=2\)被看成了两组，也说是说 对于不同的\(x,y\),视为两组结果。
小结:手动计算一下样例非常重要，可以帮我们更深刻理解题意！
2、推式子
这是一个最大公约数的典型转化技巧：把\(p\)除过来，形成：
为什么要除过来呢？因为\(p\)的取值是多种多样的，我们不知道\(p\)具体是什么，如果我们把\(p\)除过来，是不是就会简化很多呢？其实就是从骨子里想要用欧拉函数解决问题，不搞成和欧拉函数差不多的样子，怎么能用得上人家呢？ 除吧，技巧，背吧，技巧~
这是在 最大公约数中最常见的变化技巧 之一，后面还有比较难的莫比乌斯变换，以后再讲~
现在，可以视\(\large x'=\frac{x}{p},y'=\frac{y}{p}\),即\(gcd(x',y')=1\),这不就用上欧拉函数了吗？只不过数据范围有了变化，变成了\(1<=x',y'<=\frac{N}{p}\)
到了这里，\(p\)是啥呢？它是需要在\(1\sim N\)之间枚举的每一个质数，用线性筛法求得，然后遍历就可以计算了。
for (int i = 0; i < cnt; i++) {
int p = primes[i]; //枚举1~n中的所有质数p
......
}
如果\(p\)被枚举到，比如现在\(p=2\),那我们如何来求\(gcd(x',y')=1\)的数对个数呢？
这就是简单的欧拉函数+求和（可以使用前缀和优化）啊~
数据范围：\(1<=x',y'<=\frac{N}{p}\)
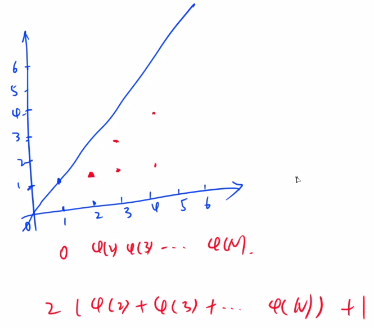
- 像\(AcWing\) \(201\) 可见的点一样，计算出前缀和,可以避免每次重复计算：
//维护前缀和
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + phi[i];
- 这里有一个第一象限\(45^。\)直线上点的问题，就是\(x'=y'\)时，分别在下方和上方计算了，需要再减去\(1\),比如\((2,2),(2,2)\)这是不行的，算重复了，减去\(1\)个。
res += s[n / p] * 2 - 1; //推导的公式
三、实现代码
#include <cstdio>
using namespace std;
typedef long long LL;
//快读
char buf[1 << 23], *p1 = buf, *p2 = buf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
const int N = 1e7 + 10; //这家伙好大啊
int primes[N], cnt;
bool st[N];
int phi[N];
LL s[N];
void euler(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] * i <= n; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) {
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
phi[i * primes[j]] = phi[i] * (primes[j] - 1);
}
}
}
int main() {
int n = read();
//利用筛法，预处理出欧拉函数值前缀和
euler(n);
//前缀和优化
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + phi[i];
LL res = 0;
for (int i = 0; i < cnt; i++)
res += s[n / primes[i]] * 2 - 1; //推导的公式
printf("%lld\n", res);
return 0;
}
四、答疑解惑
\(Q\):为什么\(AcWing\) \(201\)中可以使用\(euler(N-1)\),而本题采用的是\(euler(n)\)呢?我换成\(euler(N-1)\)发现结果不对啊？
答：因为本题除了要获取一个\(phi\)的静态结果数组外，还要用到欧拉函数筛法中的副产品\(primes\)数组,\(cnt\)变量。以此来枚举区间内所有的合法质数，对于每个质数范围内，进行求欧拉函数值，整体求和。如果我们也采用的\(N-1\)做为参数，那么这个\(cnt\)就被放大了,结果就会有问题，当然，也可以采用判断的办法进行弥补，但那样就有点啰嗦了,性能也下降为\(3639 ms\)：
#include <cstdio>
using namespace std;
typedef long long LL;
//快读
char buf[1 << 23], *p1 = buf, *p2 = buf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
const int N = 1e7 + 10;
int primes[N], cnt;
bool st[N];
int phi[N];
LL s[N];
void euler(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] * i <= n; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) {
phi[i * primes[j]] = phi[i] * primes[j];
break;
}
phi[i * primes[j]] = phi[i] * (primes[j] - 1);
}
}
for (int i = 1; i <= n; i++) s[i] = s[i - 1] + phi[i];
}
int main() {
int n = read();
euler(N - 1);
LL res = 0;
for (int i = 0; i < cnt; i++) {
if (primes[i] > n) break;
res += s[n / primes[i]] * 2 - 1;
}
printf("%lld\n", res);
return 0;
}
