P3808 【模板】AC 自动机（简单版）

\(P3808\) 【模板】\(AC\) 自动机（简单版）

AC自动机详细讲解

\(AC\)自动机真是个好东西！之前学\(KMP\)被\(Next\)指针搞晕了，所以咕了许久都不敢开\(AC\)自动机，近期学完之后，发现\(AC\)自动机并不是很难，特别是对于\(KMP\)​，个人感觉\(AC\)自动机比\(KMP\)要好理解一些，可能是因为我对树上的东西比较敏感（实际是因为我到现在都不会\(KMP\)）。

很多人都说\(AC\)自动机是在\(Trie\)树上作\(KMP\)，我不否认这一种观点，因为这确实是这样，不过对于刚开始学\(AC\)自动机的同学们就一些误导性的理解（至少对我是这样的）。\(KMP\)是建立在一个字符串上的，现在把\(KMP\)搬到了树上，不是很麻烦吗？实际上\(AC\)自动机只是有\(KMP\)的一种思想，实际上跟一个字符串的\(KMP\)有着很大的不同。

所以看这篇\(blog\)，请放下\(KMP\)，理解好\(Trie\)，再来学习。

前置技能

• \(Trie\)(很重要哦)
• \(KMP\)的思想（懂思想就可以了，不需要很熟练）

问题描述

给定\(n\)个模式串和\(1\)个文本串，求有多少个模式串在文本串里出现过。

注意:是出现过,就是出现多次只算一次。

默认这里每一个人都已经会了\(Trie\)。

我们将\(n\)个模式串建成一颗\(Trie\)树，建树的方式和建\(Trie\)完全一样。

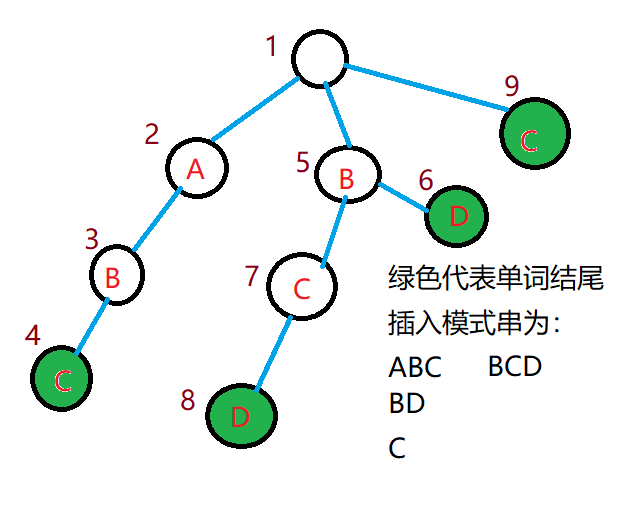
假如我们现在有文本串\(ABCDBC\)。

我们用文本串在\(Trie\)上匹配，刚开始会经过\(2、3、4\)号点，发现到\(4\)，成功地匹配了一个模式串，然后就不能再继续匹配了，这时我们还要重新继续从根开始匹配吗？

不，这样的效率太慢了。这时我们就要借用\(KMP\)的思想，从\(Trie\)上的某个点继续开始匹配。

明显在这颗\(Trie\)上，我们可以继续从\(7\)号点开始匹配，然后匹配到\(8\)。

那么我们怎么确定从那个点开始匹配呢？我们称\(i\)匹配失败后继续从\(j\)开始匹配，\(j\)是\(i\)的\(Fail\)（失配指针）。

构建\(Fail\)指针

\(Fail\)的含义

\(Fail\)指针的实质含义是什么呢？

如果一个点\(i\)的\(Fail\)指针指向\(j\)。那么\(root\)到\(j\)的字符串是\(root\)到\(i\)的字符串的一个后缀。

举个例子：（例子来自上面的图)

\(i:4\) \(j:7\)
\(root\)到\(i\)的字符串是\(ABC\)
\(root\)到\(j\)的字符串是\(BC\)
\(BC\)是\(ABC\)的一个后缀
所以\(i\)的\(Fail\)指针指向\(j\)

同时我们发现，\(C\) 也是\(ABC\)的一个后缀。

所以\(Fail\)指针指的\(j\)的深度要尽量大。

重申一下\(Fail\)指针的含义：((最长的(当前字符串的后缀))在\(Trie\)上可以查找到)的末尾编号。

感觉读起来挺绕口的蛤。感性理解一下就好了，没什么卵用的。知道\(Fail\)有什么用就行了。

求\(Fail\)

首先我们可以确定，每一个点\(i\)的\(Fail\)指针指向的点的深度一定是比\(i\)小的。（\(Fail\)指的是后缀啊）

第一层的\(Fail\)一定指的是\(root\)。（比深度\(1\)还浅的只有\(root\)了）

设点\(i\)的父亲\(fa\)的\(Fail\)指针指的是\(fafail\)，那么如果\(fafail\)有和\(i\)值相同的儿子\(j\)，那么\(i\)的\(Fail\)就指向\(j\)。这里可能比较难理解一点，建议画图理解，不过等会转换成代码就很好理解了。

由于我们在处理\(i\)的情况必须要先处理好\(fa\)的情况，所以求\(Fail\)我们使用\(BFS\)来实现。

实现的一些细节

• 1、刚开始我们不是要初始化第一层的\(fail\)指针为\(root\)，其实我们可以建一个虚节点\(0\)号节点，将\(0\)的所有儿子指向\(root\)（\(root\)编号为\(1\)，记得初始化)，然后\(root\)的\(fail\)指向\(0\)就\(OK\)了。效果是一样的。

• 2、如果不存在一个节点\(i\)，那么我们可以将那个节点设为\(fafail\)的((值和\(i\)相同)的儿子)。保证存在性，就算是\(0\)也可以成功返回到根，因为\(0\)的所有儿子都是根。

• 3、无论\(fafail\)存不存在和\(i\)值相同的儿子\(j\)，我们都可以将\(i\)的\(fail\)指向\(j\)。因为在处理\(i\)的时候\(j\)已经处理好了，如果出现这种情况，\(j\)的值是第\(2\)种情况，也是有实际值的，所以没有问题。

• 4、实现时不记父亲，我们直接让父亲更新儿子

void bfs() {
    int hh = 0, tt = -1; //将队列的头和尾变量写在这里，可以有效防止多组测试数据的初始化问题
    for (int i = 0; i < 26; i++)
        if (tr[0][i]) q[++tt] = tr[0][i];

    while (hh <= tt) {
        int p = q[hh++];
        for (int i = 0; i < 26; i++) {
            int t = tr[p][i]; // p状态，通过i这条边，到达的新状态t; 也可以理解为是前缀

            if (!t)
                tr[p][i] = tr[ne[p]][i]; //节点 指向父节点失配指针的i这条边
            else {
                ne[t] = tr[ne[p]][i]; //失配指针指向父节点失配指针的i这条边
                q[++tt] = t;          //存在的要入队列
            }
        }
    }
}

查询

求出了\(Fail\)指针，查询就变得十分简单了。

为了避免重复计算，我们每经过一个点就打个标记为\(-1\)，下一次经过就不重复计算了。

同时，如果一个字符串匹配成功，那么他的\(Fail\)也肯定可以匹配成功（后缀嘛），于是我们就把\(Fail\)再统计答案，同样，\(Fail\)的\(Fail\)也可以匹配成功，以此类推……经过的点累加\(flag\)，标记为\(-1\)。

最后主要还是和\(Trie\)的查询是一样的。

int res = 0;
for (int i = 0, j = 0; s[i]; i++) {
    j = tr[j][s[i] - 'a']; //从j点出发，经t这条边,重复利用变量j，不断的移动游标j
    //沿着失配指针不断向上，累加匹配值
    for (int p = j; p && ~cnt[p]; p = ne[p]) res += cnt[p], cnt[p] = -1;
}

完整代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;
const int N = 1000010;

int n;     // n个模式串
char s[N]; //模式串
char T[N]; //文本串

// Trie树
int tr[N][26], idx;
int cnt[N];
void insert(char *s, int x) {
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int t = s[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++idx;
        p = tr[p][t];
    }
    cnt[p]++; //以p为结束节点的字符串个数+1,如果有重复的，这里++也是OK的~
}

// AC自动机
int q[N], ne[N];
void bfs() {
    int hh = 0, tt = -1;
    for (int i = 0; i < 26; i++)
        if (tr[0][i]) q[++tt] = tr[0][i];

    while (hh <= tt) {
        int p = q[hh++];
        for (int i = 0; i < 26; i++) {
            int t = tr[p][i]; //此处直接优化为Trie图，没有采用原始的while向上递归处理的办法，记忆这个版本即可
            if (!t)
                tr[p][i] = tr[ne[p]][i];
            else {
                ne[t] = tr[ne[p]][i];
                q[++tt] = t;
            }
        }
    }
}

//查询字符串s中 n个模式串出现了几个
int query(char *s) {
    int p = 0;
    int res = 0;
    for (int i = 0; s[i]; i++) {
        p = tr[p][s[i] - 'a'];
        for (int j = p; j; j = ne[j]) {
            if (cnt[j] == -1) break;
            res += cnt[j];
            cnt[j] = -1;
        }
    }
    return res;
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    //构建Trie树
    for (int i = 1; i <= n; i++) {
        cin >> s;
        insert(s, i);
    }
    //构建AC自动机
    bfs();
    //输入文本串
    cin >> T;
    //输出模式串出现的个数（注意：不是次数，是个数）
    printf("%d\n", query(T));
    return 0;
}