AcWing 253. 普通平衡树
. 普通平衡树
一、题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 1 插入数值 。
- 2 删除数值 (若有多个相同的数,应只删除一个)。
- 3 查询数值 的排名(若有多个相同的数,应输出最小的排名)。
- 4 查询排名为 的数值。
- 5 求数值 的前驱(前驱定义为小于 的最大的数)。
- 6 求数值 的后继(后继定义为大于 的最小的数)。
注意: 数据保证查询的结果一定存在。
输入格式
第一行为 ,表示操作的个数。
接下来 行每行有两个数 和 , 表示操作的序号()。
输出格式
对于操作 每行输出一个数,表示对应答案。
数据范围
,所有数均在 到 内。
输入样例:
8
1 10
1 20
1 30
3 20
4 2
2 10
5 25
6 -1
输出样例:
2
20
20
20
二、
和我一起大声读:大法好! ,比平衡树慢一倍左右。
#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
int n;
vector<int> a;
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
int op, x;
while (n--) {
cin >> op >> x;
if (op == 1)
a.insert(lower_bound(a.begin(), a.end(), x), x); //插入数值x
else if (op == 2)
a.erase(lower_bound(a.begin(), a.end(), x)); //删除数值x
else if (op == 3)
printf("%d\n", lower_bound(a.begin(), a.end(), x) - a.begin() + 1); //查询数值 x 的排名
else if (op == 4)
printf("%d\n", a[x - 1]); //查询排名为 x 的数值
else if (op == 5)
printf("%d\n", *--lower_bound(a.begin(), a.end(), x)); //求数值 x 的前驱
else if (op == 6)
printf("%d\n", *upper_bound(a.begin(), a.end(), x)); //求数值 x 的后继
}
return 0;
}
三、普通平衡树
本题是一道普通平衡树的引入模板题,是想让我们了解并开始学习平衡树的,用水过,一来可以让大家更好的学习,二来是没有背下来普通平衡树、树、之前,有一技傍身,废话少说,开始操练:
指 ,又叫作 树堆,同时满足二叉搜索树和堆两种性质。二叉搜索树满足中序有序性,输入序列不同,创建的二叉搜索树也不同,在 最坏的情况 下(只有左子树或只有右子树)会退化为 线性。例如输入1 2 3 4 5,创建的二叉搜索树如下图所示。
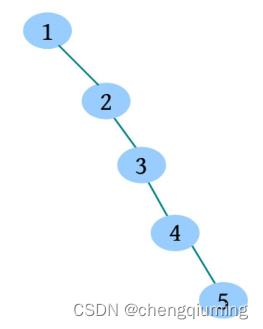
二叉搜索树 的插入、查找、删除等效率与树高成正比,因此在创建二叉搜索树时 要尽可能通过调平衡压缩树高。平衡树有很多种,例如 树、伸展树、、红黑树等,这些调平衡的方法相对复杂。
若一个二叉搜索树插入节点的顺序是随机的,则得到的二叉搜索树在大多数情况下是平衡的,即使存在一些极端情况,这种情况发生的概率也很小,因此 以随机顺序创建的二叉搜索树,其期望高度为。这是有数学定理证明过的,水平所限,不再详细论述。所以,可以将输入数据随机打乱,再创建二叉搜索树,但我们有时并不能事前得知所有待插入的节点,而可以有效解决该问题。
在 的构建过程中,插入节点时会给每个节点都 附加一个随机数作为优先级,该优先级满足堆的性质(最大堆或最小堆均可,这里以 最大堆为例,根的优先级大于左右子节点),数值满足二叉搜索树性质(中序有序性,左子树小于根,右子树大于根)。
的中序遍历 投影法则
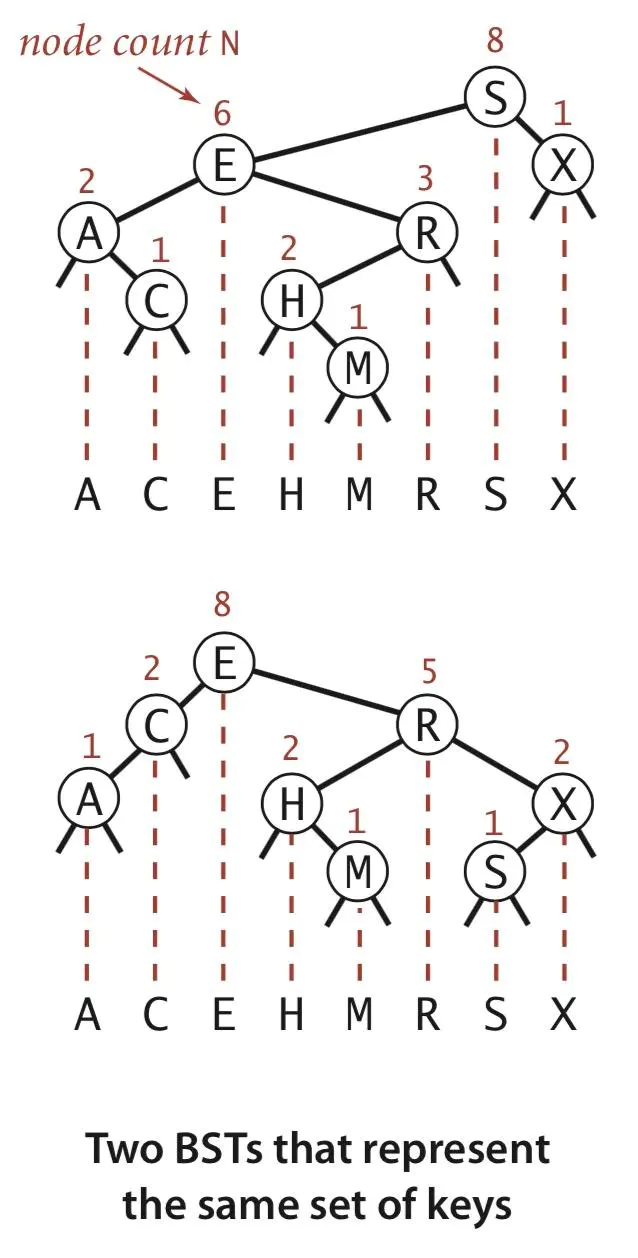
同样的中序遍历输出其实在真正的存储时,是不一样的形态。我们只要维持住中序遍历的次序不变,结合大顶堆的随机值在上的特点,就可以得到一个 矮粗胖 的平衡树,获取最好的性能。
构建过程
输入 6 4 9 7 2,构建 。首先给每个节点都附加一个随机数作为优先级,根据 输入数据 和 附加随机数,构建的 如下图所示。

右旋和左旋
需要两种神操作,通过两个神操作,才能保证平衡树不是一条链,而是又矮又胖,这两个神操作是:右旋和左旋
右旋()
节点 右旋时,会携带自己的右子树,向右旋转到 的右子树位置, 的右子树被抛弃,此时 右旋后左子树正好空闲,将 的右子树放在 的左子树位置,旋转后的树根为 。

动画演示:
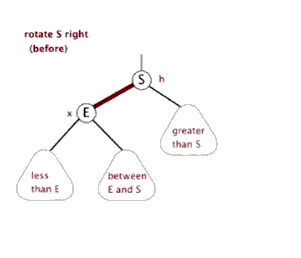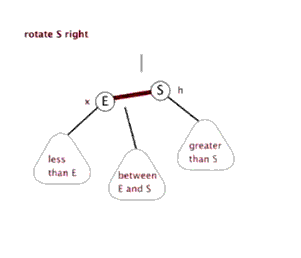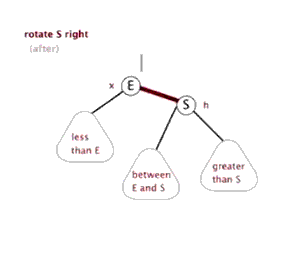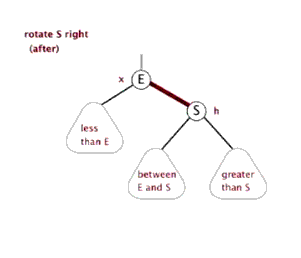
左旋()
节点 左旋时,携带自己的左子树,向左旋转到 的左子树位置, 的左子树被抛弃,此时 左旋后右子树正好空闲,将 的左子树放在 的右子树位置,旋转后的树根为 。

动画演示:
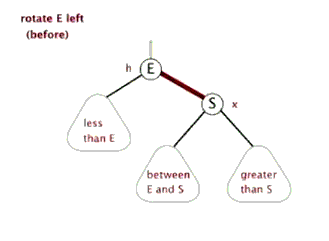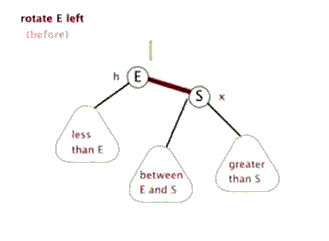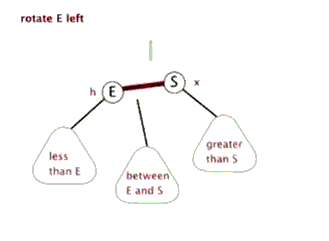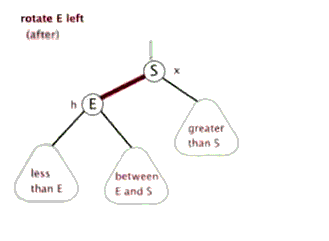
插入
的插入操作和二叉搜索树一样,首先根据有序性找到插入的位置,然后创建新节点插入该位置。创建新节点时,会给该节点附加一个随机数作为优先级,自底向上检查 该优先级是否满足堆性质,若不满足,则需要右旋或左旋,使其满足堆性质。
算法步骤:
-
① 从根节点 开始,若 为空,则创建新节点,将待插入元素 存入新节点,并给新节点附加一个随机数作为优先级
-
② 若 等于 ,则
-
③ 若 小于 ,则在 的左子树中递归插入。回溯时做旋转调整,若 ,则 右旋
-
④ 若 大于 ,则在 的右子树中递归插入。回溯时做旋转调整,若 ,则 左旋
一个树堆如下图所示,在该树堆中插入元素 ,插入过程如下:
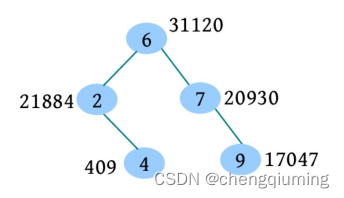
(1)根据二叉搜索树的插入操作,将 插入 的左子节点位置,假设 的随机数优先级为 。
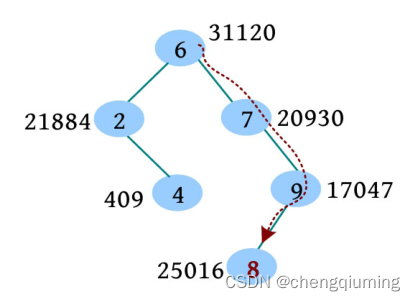
(2)回溯时,判断是否需要旋转, 的优先级比其左子节点小,因此 节点右旋。

(3)继续向上判断, 的优先级比 的右子节点小,因此节点左旋。
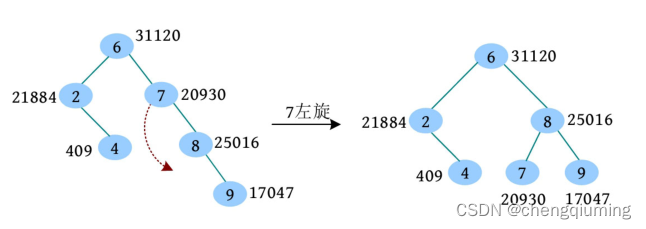
(4)继续向上判断, 的优先级不比 的左右子节点小,满足最大堆性质,无须调整,已向上判断到树根,算法停止。
删除
的删除操作 :找到待删除的节点,将该节点向优先级大的子节点旋转,一直旋转到叶子,直接删除叶子即可。
算法步骤
-
从根节点 开始,若待删除元素 等于 ,则:
- 若 只有左子树或只有右子树,则令其子树子承父业代替 ,返回;
- 若 ,则 右旋,继续在 的 右子树中递归 删除
- 若 ,则 左旋,继续在 的 左子树中递归 删除
-
若 ,则在 的 左子树中递归 删除
-
若 ,则在 的 右子树中递归 删除
在上面的树堆中删除元素 ,删除过程如下:
(1)根据二叉搜索树的删除操作,首先找到 的位置, 的右子节点优先级大, 左旋。
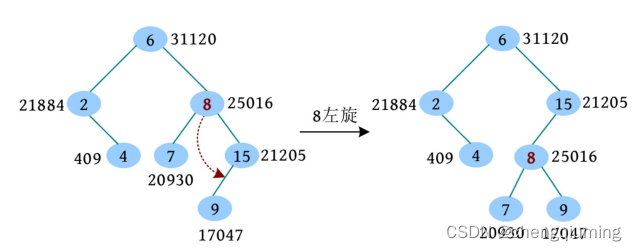
(2)接着判断, 的左子节点优先级大, 右旋。
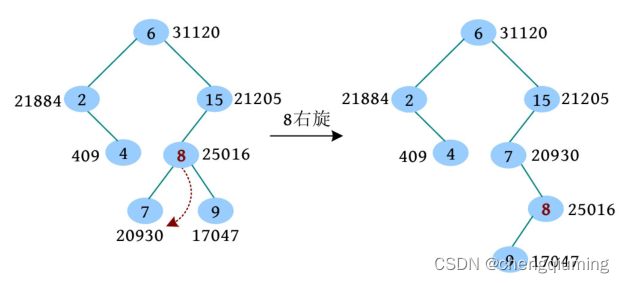
(3)此时 只有一个左子树,左子树子承父业代替它
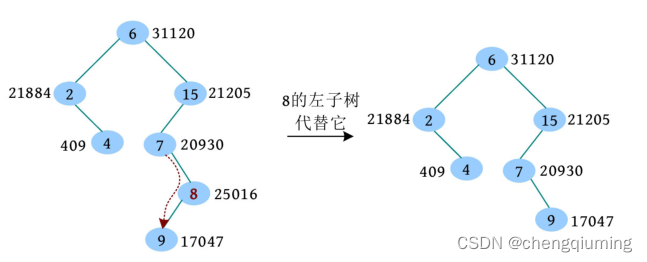
前驱
在 中求一个节点 的前驱时,首先从树根开始,若当前节点的值小于 ,则用 暂存该节点的值,在当前节点的右子树中寻找,否则在当前节点的左子树中寻找,直到当前节点为空,返回 ,即为 的前驱。
后继
在 中求一个节点 的后继时,首先从树根开始,若当前节点的值大于 ,则用 暂存该节点的值,在当前节点的左子树中寻找,否则在当前节点的右子树中寻找,直到当前节点为空,返回 ,即为 的后继。
三、实现代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, INF = 1e8;
int n;
struct Node {
int l, r; // 左右儿子节点号
int key, val; // BST中的真实值,堆中随机值
int cnt, size; // 当前数字个数,小于等于当前数字的数字个数总和
} tr[N];
int root, idx;
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt; // BST左子树数字个数+右子树数字个数+自己数字个数
}
int get_node(int key) {
tr[++idx].key = key; //填充 BST的值
tr[idx].val = rand(); //堆中的随机值
tr[idx].cnt = tr[idx].size = 1;
return idx;
}
//右旋
void zig(int &p) {
int q = tr[p].l;
tr[p].l = tr[q].r;
tr[q].r = p;
p = q;
pushup(tr[p].r), pushup(p);
}
//左旋
void zag(int &p) {
int q = tr[p].r;
tr[p].r = tr[q].l;
tr[q].l = p;
p = q;
pushup(tr[p].l), pushup(p);
}
void build() {
get_node(-INF), get_node(INF);
root = 1, tr[1].r = 2;
pushup(root);
if (tr[1].val < tr[2].val) zag(root);
}
void insert(int &p, int key) {
if (!p)
p = get_node(key);
else if (tr[p].key == key)
tr[p].cnt++;
else if (tr[p].key > key) {
insert(tr[p].l, key); //往左边插入
if (tr[tr[p].l].val > tr[p].val) zig(p); //左儿子大,右旋
} else {
insert(tr[p].r, key); //往右边插入
if (tr[tr[p].r].val > tr[p].val) zag(p); //右儿子大,左旋
}
pushup(p);
}
void remove(int &p, int key) {
if (!p) return; //如果发现p==0, 就是没找着
if (tr[p].key == key) { //如果找着了
if (tr[p].cnt > 1) //并且不止1个,这个就简单了,去掉一个就行了,记得 pushup
tr[p].cnt--;
else if (tr[p].l || tr[p].r) { //如果只有1个,并且,有左儿子或右儿子,这时不能直接删除掉,需要处理一下
if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) { //如果没有右儿子,或者是左儿子的随机值大于右儿子随机值,右旋
zig(p); //右旋后,此值向右运动,继续递归右子树处理
remove(tr[p].r, key);
} else {
zag(p); //左旋,此值向左运动,继续递归向左子树处理
remove(tr[p].l, key);
}
} else
p = 0; //左右都没有子树,直接标识为删除
} else if (tr[p].key > key) //如果在左
remove(tr[p].l, key);
else
remove(tr[p].r, key); //如果在右
//向上更新统计信息
pushup(p);
}
int get_rank(int p, int key) { // 通过数值找排名
if (!p) return 0; // 本题中不会发生此情况
if (tr[p].key == key) return tr[tr[p].l].size + 1;
if (tr[p].key > key) return get_rank(tr[p].l, key);
return tr[tr[p].l].size + tr[p].cnt + get_rank(tr[p].r, key);
}
int get_key(int p, int rank) { // 通过排名找数值
if (!p) return INF; // 本题中不会发生此情况
if (tr[tr[p].l].size >= rank) return get_key(tr[p].l, rank);
if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
return get_key(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}
int get_prev(int p, int key) { // 找到严格小于key的最大数
if (!p) return -INF;
if (tr[p].key >= key) return get_prev(tr[p].l, key);
return max(tr[p].key, get_prev(tr[p].r, key)); //当前位置可能成为答案
}
int get_next(int p, int key) { // 找到严格大于key的最小数
if (!p) return INF;
if (tr[p].key <= key) return get_next(tr[p].r, key);
return min(tr[p].key, get_next(tr[p].l, key));
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
build();
cin >> n;
while (n--) {
int op, x;
cin >> op >> x;
if (op == 1)
insert(root, x);
else if (op == 2)
remove(root, x);
else if (op == 3)
printf("%d\n", get_rank(root, x) - 1);
else if (op == 4)
printf("%d\n", get_key(root, x + 1));
else if (op == 5)
printf("%d\n", get_prev(root, x));
else
printf("%d\n", get_next(root, x));
}
return 0;
}
四、 树堆
,以下简写为,是一种(树堆)的变体,功能比强大,代码比好写,易于理解,常数稍大.
不需要 通过一般平衡树的 左右旋转 来保持平衡,而是通过 分裂 和 合并 来实现操作。
结构
以结构体作为树的每一个节点,存储:
- ① 左子树位置
- ② 右子树的位置
- ③ 权值
- ④ 堆中随机索引
- ⑤ 子树大小.一般子树大小用于查排名和查值
root是树根编号,idx是点的编号.
struct Node {
int l, r; // 左右子树编号
int key, val; // key权 val堆权
int size; // 子树大小
} tr[N];
int root, idx;
fhq和treap一样满足treap的性质,也就是 既是,又是 随机权值的堆.
至于为什么满足堆的性质的就能平衡,有如下定理保证:
一颗有个不同关键字随机构建的的期望高度为.
随机堆的权值正是模拟了随机构建,所以是平衡的,同理也平衡.
创建节点和更新子树大小
int get_node(int key) {
tr[++idx].key = key;
tr[idx].val = rnd();
tr[idx].size = 1;
return idx;
}
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
}
子树大小由两侧子树和根节点更新.rnd()为随机值产生函数。
首先是一个二叉搜索树(),它的每个节点有两个主要信息:和,是我们要维护的键值,而是随机生成的,信息主要用于我们对于题目信息的处理,而则是用于维持在结构上满足期望高度为的。 除了要满足关于的性质之外,还需满足关于的 小根堆 性质。就是说,对于任意中的节点 :
-
其左子树上的所有节点的 小于等于 节点的值, 节点所有右子树上所有节点的 大于等于 节点的值
-
对于任意节点 ,其左、右儿子的值 大于等于 的值(满足 小根堆 的性质)
要牢牢记住这两点的区别,否则会像我一样搞混,然后写代码的时候狂 ,。下面给出一颗:

上图就是一颗,其中每个节点中的数字为,每个节点下方的数字为当前节点的。可以发现一颗中序遍历后得到的序列是单调递增。 这里,我们要引入的两个基本操作:和, 其中是分离操作,是合并操作,下面我们来一一阐明:
1. 操作
通常情况下, 用于分离一颗,对于一个元素 ,我们会将这棵分裂为左右两棵树,左树上每个节点的值都小于等于 , 而右树上的所有节点的值都大于 ;下面给出代码:
//将以p为根的平衡树进行分裂,小于等于key的都放到以x为根的子树中,大于key放到以y为根的子树中
void split(int p, int key, int &x, int &y) {
if (!p) { //当前节点为空
x = y = 0;
return;
}
if (tr[p].key <= key)
x = p, split(tr[p].r, key, tr[p].r, y); // x确定了,左边确定了,但右边未确定,需要继续递归探索
else
y = p, split(tr[p].l, key, x, tr[p].l); // y确定了,右边确定了,但左边未确定,需要继续递归探索
pushup(p); //更新统计信息
}
以上代码如果学过线段树的话会好理解的多,本蒟蒻也建议先去熟练掌握线段树再来学习,这样会轻松很多。下面我们来模拟这个过程—— 本蒟蒻就是开始没有自己去模拟,导致一直不是很理解的实现方式。
对于上图,假如我们要将其分离为小于等于和大于两个部分:
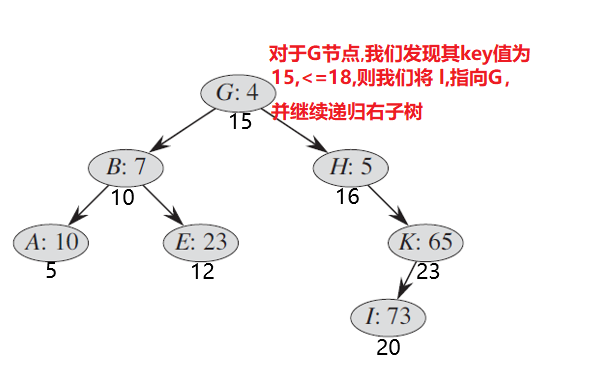
经过此役,的指向已经很清楚了,就是,因为左侧的所有数,都会比小,所以左子树的范围也就相应继承下来了:不需要动,但的右边界不没有确定,因为到底应该在右子树的哪个位置割开呢?还需要继续研究,继续递归解决。
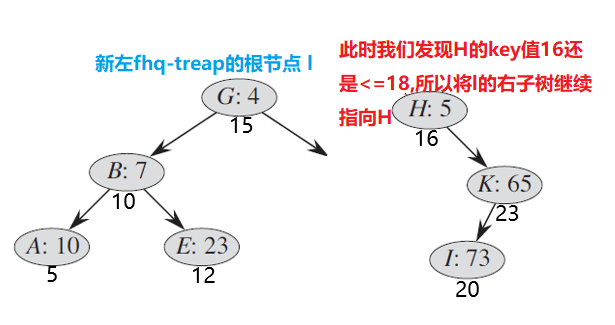
经过此役, 的右边界还在不断的修改,不断的向右逼近。
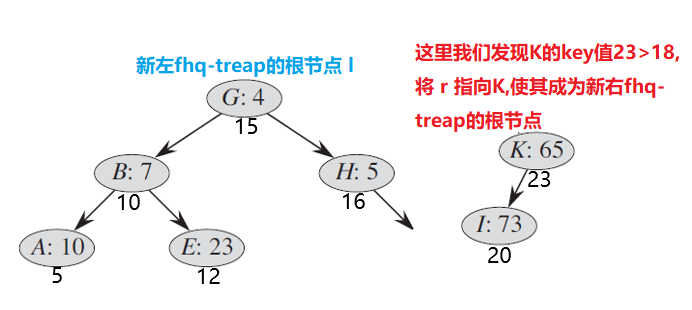
经过此役,出现了第一个大于的点,那么此点做为一个有代表性的点,被设置为。同时,的右边界,的左边界依然不明,需要继续递归查找。分裂节点的左子树,由于节点的权值,所以我们将 节点归入右,接下来我们会碰到空节点,递归将会跳出,这时,我们就能得到左右两棵了:
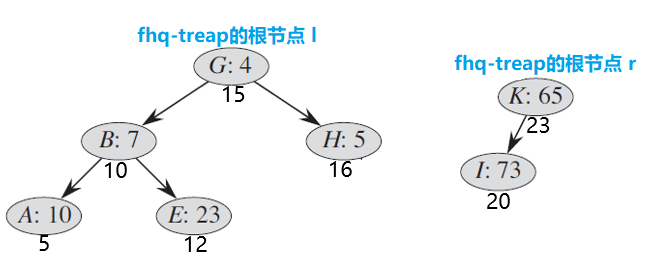
以上就是的基本操作之一操作的全部过程了 。
. 操作
这是一个合并操作,但它也不能随便合并,如果要合并两棵,那么它们可以进行合并当且仅当左上所有节点的值都小于等于右中的最小值(也就是左树小于等于右树)或两棵树中有空树。 这个性质很重要,为根据合并两棵树做好的前提,保证了结构不会因合并而被破坏。 合并时,我们会根据左右两棵树的根节点的值大小进行合并,大家先看一下代码:
//将以x,y为根的两个子树合并成一棵树.要求x子树中所有key必须小于等于y子树中所有key
int merge(int x, int y) {
if (!x || !y) return x + y; //如果x或者y有一个是空了,那么返回另一个即可
int p; //根,返回值
if (tr[x].val > tr[y].val) { // x.key<y.key,并且, tr[x].val > tr[y].val, x在y的左上,此时理解为大根堆,y向x的右下角合并
p = x;
tr[x].r = merge(tr[x].r, y);
} else {
p = y;
tr[y].l = merge(x, tr[y].l); //复读机
}
pushup(p); //更新统计信息
return p;
}
还是一样,画图好理解:
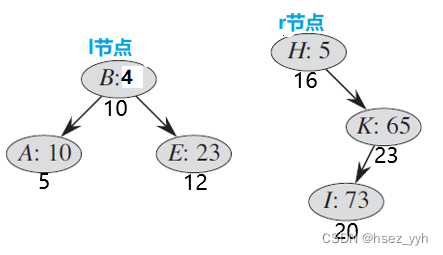
以上是两棵要合并的
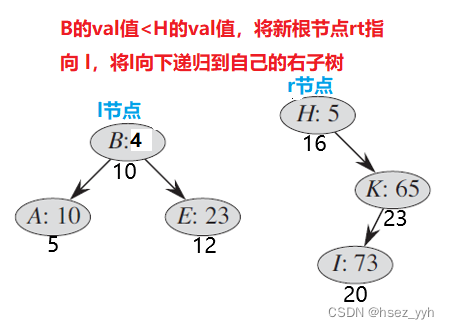
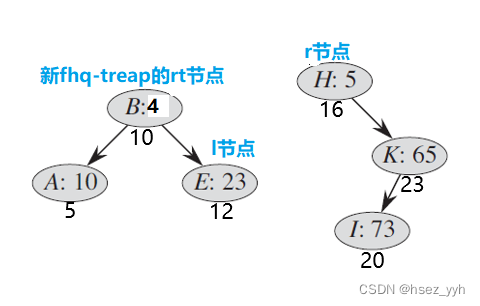
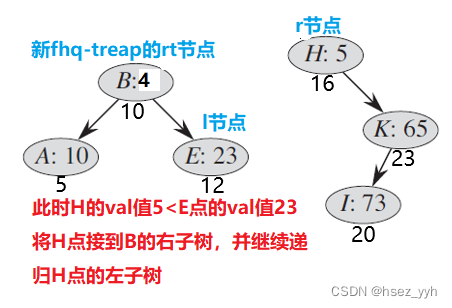
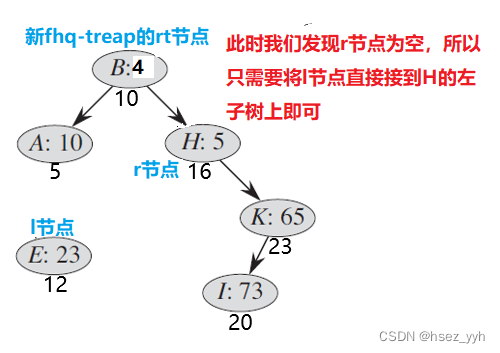
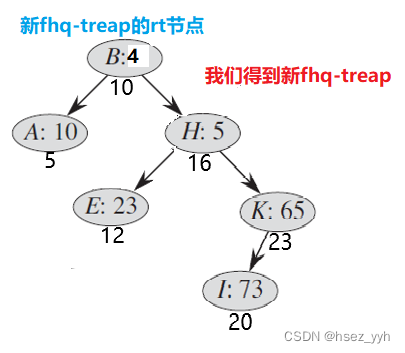
以上就是合并的全部过程了。
六、实现代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
//普通Treap 316 ms
// FHQ Treap 433 ms
//两者基本在一个数量级上,常数略大
using namespace std;
const int N = 1e5 + 10;
struct Node {
int l, r; //左右儿子的节点号
int key; // BST中的真实值
int val; //堆中随机值,用于防止链条化
int size; //小于等于 key的数字个数,用于计算rank等属性
} tr[N];
int root, idx; //用于动态开点,配合tr记录FHQ Treap使用
int x, y, z; //本题用的三个临时顶点号
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1; //合并信息
}
int get_node(int key) { //创建一个新节点
tr[++idx].key = key; //创建一个新点,值为key
tr[idx].val = rand(); //随机一个堆中索引号
tr[idx].size = 1; //新点,所以小于等于它的个数为1个,只有自己
return idx; //返回点号
}
//将以p为根的平衡树进行分裂,小于等于key的都放到以x为根的子树中,大于key放到以y为根的子树中
void split(int p, int key, int &x, int &y) {
if (!p) { //当前节点为空
x = y = 0;
return;
}
if (tr[p].key <= key)
x = p, split(tr[p].r, key, tr[p].r, y); // x确定了,左边确定了,但右边未确定,需要继续递归探索
else
y = p, split(tr[p].l, key, x, tr[p].l); // y确定了,右边确定了,但左边未确定,需要继续递归探索
pushup(p); //更新统计信息
}
//将以x,y为根的两个子树合并成一棵树.要求x子树中所有key必须小于等于y子树中所有key
int merge(int x, int y) {
if (!x || !y) return x + y; //如果x或者y有一个是空了,那么返回另一个即可
int p; //根,返回值
if (tr[x].val > tr[y].val) { // x.key<y.key,并且, tr[x].val > tr[y].val, x在y的左上,此时理解为大根堆,y向x的右下角合并
p = x;
tr[x].r = merge(tr[x].r, y);
} else {
p = y;
tr[y].l = merge(x, tr[y].l); //复读机
}
pushup(p); //更新统计信息
return p;
}
void insert(int key) {
split(root, key, x, y); //按k分割
root = merge(merge(x, get_node(key)), y); //在x与key节点合并,再与key合并
}
void remove(int key) {
split(root, key, x, z);
split(x, key - 1, x, y);
// x<=key ,再分x <= key - 1,y就是=key的树
y = merge(tr[y].l, tr[y].r); //删除y点(根)
root = merge(merge(x, y), z); //合并x,y,z
}
int get_rank(int key) { //按值查排名
split(root, key - 1, x, y); //按key-1分割,x子树大小+1就是排名
int rnk = tr[x].size + 1; //储存x的大小+1
root = merge(x, y);
return rnk;
}
int get_key(int rnk) { //按排名查值
int p = root;
while (p) {
if (tr[tr[p].l].size + 1 == rnk)
break; //找到排名了
else if (tr[tr[p].l].size >= rnk)
p = tr[p].l; //当前size>=rank,去左子树
else {
//去右子树中找rank -= 左子树大小+1(根)的排名
rnk -= tr[tr[p].l].size + 1;
p = tr[p].r;
}
}
return tr[p].key;
}
//返回<key的最大数
int get_prev(int key) {
split(root, key - 1, x, y); //按key-1分,x最右节点就是前驱
int p = x;
while (tr[p].r) p = tr[p].r; //向右走
int res = tr[p].key;
root = merge(x, y);
return res;
}
//返回>key的最小数
int get_next(int key) {
split(root, key, x, y); //按key分y最左节点是后继
int p = y;
while (tr[p].l) p = tr[p].l;
int res = tr[p].key;
root = merge(x, y);
return res;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
int q;
cin >> q;
while (q--) {
int op, x;
cin >> op >> x;
if (op == 1)
insert(x);
else if (op == 2)
remove(x);
else if (op == 3)
printf("%d\n", get_rank(x));
else if (op == 4)
printf("%d\n", get_key(x));
else if (op == 5)
printf("%d\n", get_prev(x));
else if (op == 6)
printf("%d\n", get_next(x));
}
return 0;
}
七、待研习
平衡树进阶博文
【模板】普通平衡树 - 洛谷
【模板】文艺平衡树 - 洛谷
AcWing 266. 超级备忘录 - AcWing题库
[NOI2005] 维护数列 - 洛谷
【模板】可持久化平衡树 - 洛谷
【模板】可持久化文艺平衡树 - 洛谷
【模板】二逼平衡树(树套树)
FHQ-Treap(非旋treap/平衡树)——从入门到入坟



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2018-05-07 云平台丢失文件的查找办法
2015-05-07 在lua中正确使用uuid的方法:
2013-05-07 Mysql 备份工具 XtraBackup 2.0.7 发布