GSS5 - Can you answer these queries V

\(GSS5\) - \(Can\) \(you\) \(answer\) \(these\) \(queries\) \(V\)

洛谷

一、题目大意

对于长度为\(n\)的序列，回答\(m\)个询问，每个询问查询左端点在\([x_1,y_1]\)之中,右端点在\([x_2,y_2]\)之中的所有区间和的最大值，即：

\[\large \max_{x_1<x<x_2,y_1<y<y_2}\sum_{i=l}^ja[i] \]

(其中保证\(l_1\leq l_2;r_1\leq r_2;n,m,|a[i]|\leq 1e4\)).

二、题目解析

通过分类讨论解决:

• \(y_1<x_2\)
  即两个区间没有重合部分

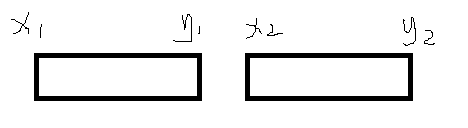
此时，我们只有一种选择方案：

区间 \([x_1,y_1]\) 找到右起最大子段和，区间 \([y_1+1,x_2-1]\) 的区间和，区间 \([x_2,y_2]\) 找到左起最大子段和，三者相加就是这个询问的答案

注：为了保证左右端点必须在\((x_1,y_1),(x_2,y_2)\)两个范围内，所以，中间你不想要也不行，只能硬着头皮上。

• \(y_1\ge x_2\)
  ​如图：

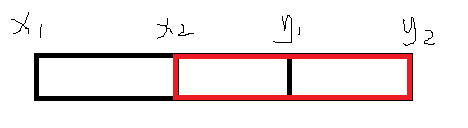
两个区间有重叠，那我们就不能考虑一种方案了。

分三种情况：

• 区间 \([x_2,y_1]\) 的 区间最大子段和
• 区间 \([x_1,x_2]\) 的 右起最大子段和 + 区间 \([x_2,y_2]\) 的 左起最大子段和
• 区间 \([y_1,y_2]\) 的 左起最大子段和 + 区间 \([x_1,y_1]\) 的 右起最大子段和

这样这个询问的最优解就一定被计算到了，保证了答案的最优。

最后，就能保证所有的询问都是最优的答案。

三、实现代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>

using namespace std;
const int N = 10010;

int a[N];
struct Node {
    int l, r;
    int sum, tmax, lmax, rmax;
} tr[N << 2];

void calc(Node &u, Node &l, Node &r) {
    u.sum = l.sum + r.sum;                           // 区间和
    u.tmax = max({l.tmax, r.tmax, l.rmax + r.lmax}); // 子区间最大值
    u.lmax = max(l.lmax, l.sum + r.lmax);            // 左前缀最大值
    u.rmax = max(r.rmax, r.sum + l.rmax);            // 右后缀最大值
}
void pushup(int u) {
    calc(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    tr[u] = {l, r, 0, 0, 0, 0};

    if (l == r) {
        tr[u].sum = tr[u].tmax = tr[u].lmax = tr[u].rmax = a[l];
        return;
    }

    int mid = (tr[u].l + tr[u].r) >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

Node query(int u, int l, int r) {
    if (l > tr[u].r || r < tr[u].l) return {}; // 递归出口，不在我管辖范围内的情况，返回0
    if (l <= tr[u].l && tr[u].r <= r) return tr[u];

    int mid = (tr[u].l + tr[u].r) >> 1;
    if (r <= mid) return query(u << 1, l, r);
    if (l > mid) return query(u << 1 | 1, l, r);

    Node a = query(u << 1, l, r), b = query(u << 1 | 1, l, r), c;
    calc(c, a, b);
    return c;
}
int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    int T, n, m;
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> a[i];
        build(1, 1, n);

        cin >> m;
        while (m--) {
            int x1, y1, x2, y2, res;
            Node a, b, c;
            cin >> x1 >> y1 >> x2 >> y2;
            if (y1 < x2) { // 这里不能取等 不然边界会被算2次
                a = query(1, x1, y1);
                b = query(1, x2, y2);
                c = query(1, y1 + 1, x2 - 1);
                res = a.rmax + c.sum + b.lmax;
            } else {
                res = query(1, x2, y1).tmax; // 最大子序列和出现在交集中

                a = query(1, x1, x2 - 1);
                b = query(1, x2, y2);
                res = max(res, a.rmax + b.lmax);

                a = query(1, x1, y1);
                b = query(1, y1 + 1, y2);
                res = max(res, a.rmax + b.lmax);
            }
            printf("%d\n", res);
        }
    }
    return 0;
}