AcWing 352 . 闇の連鎖
\(AcWing\) \(352\) . 闇の連鎖
一、题目描述
传说中的暗之连锁被人们称为 \(Dark\)。
\(Dark\) 是人类内心的黑暗的产物，古今中外的勇者们都试图打倒它。
经过研究，你发现 \(Dark\) 呈现 无向图 的结构，图中有 \(N\) 个节点和两类边，一类边被称为 主要边，而另一类被称为 附加边。
\(Dark\) 有 \(N–1\) 条主要边，并且 \(Dark\) 的任意两个节点之间都存在一条只由主要边构成的路径。
另外，\(Dark\) 还有 \(M\) 条附加边。
你的任务是把 \(Dark\) 斩为不连通的两部分。 [提示我们：最小生成树]
① 一开始 \(Dark\) 的附加边都处于无敌状态，你只能选择一条主要边切断。
一旦你切断了一条主要边，\(Dark\) 就会进入防御模式，主要边会变为无敌的而附加边可以被切断。
② 但是你的能力只能再切断 \(Dark\) 的一条附加边。
现在你想要知道，一共有多少种方案可以击败 \(Dark\)。
注意，就算你第一步切断主要边之后就已经把 \(Dark\) 斩为两截，你也需要切断一条附加边才算击败了 \(Dark\)。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
之后 \(N–1\) 行，每行包括两个整数 \(A\) 和 \(B\)，表示 \(A\) 和 \(B\) 之间有一条主要边。
之后 \(M\) 行以同样的格式给出附加边。
输出格式
输出一个整数表示答案。
二、题目分析
首先梳理下题意，一个无向图中，有\(N - 1\)条主要边，这么多主要边构成了原图的一棵支撑树。同时还有\(M\)条附加边，每条附加边都会增加一个回路。我们需要做的就是将原图斩为两个不连通的部分，并且需要切断两条边，第一条边必须是主要边，第二条边必须是附加边。
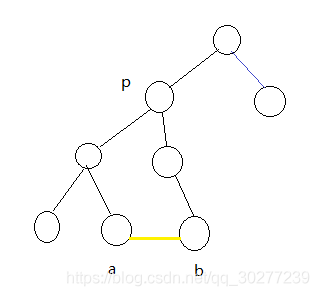
如上图所示，黑色线条连接的边就是主要边，黄色线条连接的边就是附加边。
易知主要边构成了树结构，我们可以依次考虑每个附加边（每次只考虑一条附加边，当其它附加边不存在），然后考虑附加边和树边构成的环。对于这个环上的树边而言，删掉它们之中的任一条后，只能再将那条附加边删掉才能击败\(Dark\)。
可以这样考虑，我们规定树边有一个权值，该权值初始为\(0\)，每次枚举一个附加边的时候，都将其所在环的树边的权值加\(1\)。那么在枚举完毕所有附加边之后，权值为\(0\)的边是那种只要将其删去，就直接能击败\(Dark\)（因为它不在任何一个含附加边的环里），所以第一步删去它的方案数有\(M\)个；权值为\(1\)的边是那种将其删去后，还需要删掉\(1\)条附加边才能击败\(Dark\)，所以第一步删去它的方案数有\(1\)个；而权值大于\(1\)的边是删去之后无法击败\(Dark\)。
所以问题转化为如何 快速实现 将树上的某条路径权值都加上某个数\(c\)，和如何求出每条边最后的权值。这可以用 树上差分(边权) 来做：
构造一个差分树，该树和原树的点集和边集一模一样。先对每个点\(v\)开一个点权\(d[v]\)，初始为\(0\)，如果要将路径\(a\sim b\)这条树上路径的所有边权重都加上\(c\)，那么我们可以将\(d[a]\)和\(d[b]\)都加上\(c\)，并且\(a\)和\(b\)的最近公共祖先\(p\)的点权\(d[p]\)减去\(2c\)。那么原树某条边的边权就等于差分树中该边指向的深度更深的节点的子树点权之和。
\(1\).主要边被覆盖了\(0\)次,即上面只有\(0\)条附加边.
我们发现删除完这条主要边后,随意删除一条附加边,我们都可以让树不连通.也就是\(m\)种方案.
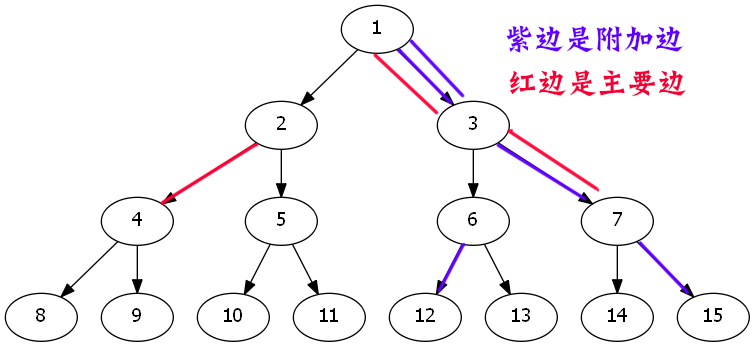
只要删除\((2,4)\)这条红边,那么随意一条附加边,都可以满足条件.
\(2\).主要边覆盖\(1\)次,即上面只有一条附加边
我们发现删除完这条主要边后,我们只能删除这条主要边的附加边.也就是\(1\)种方案.
也就是删除咱们图上面的\((3,7)\)红边,然后我们只能删除那条上面的紫色边.
\(3\).主要边覆盖大于\(1\)次,即上面有多条附加边
我们发现,怎么删除,总能连通.于是\(0\)种方案.
二、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010;
int depth[N], f[N][25];
int n, m;
int dlt[N]; //差分数组
int ans; //存答案
const int T = 22;
//邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
//树上倍增
void bfs() {
queue<int> q;
q.push(1);
depth[1] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!depth[j]) {
depth[j] = depth[u] + 1;
q.push(j);
f[j][0] = u;
for (int k = 1; k <= T; k++) f[j][k] = f[f[j][k - 1]][k - 1];
}
}
}
}
//标准lca
int lca(int a, int b) {
if (depth[a] < depth[b]) swap(a, b);
for (int i = T; i >= 0; i--)
if (depth[f[a][i]] >= depth[b]) a = f[a][i];
if (a == b) return a;
for (int i = T; i >= 0; i--)
if (f[a][i] != f[b][i])
a = f[a][i], b = f[b][i];
return f[a][0];
}
//前缀和
void dfs(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
dlt[u] += dlt[j];
}
}
int main() {
int a, b;
scanf("%d %d", &n, &m);
memset(h, -1, sizeof h);
for (int i = 1; i < n; i++) { // n-1条边
scanf("%d %d", &a, &b);
add(a, b), add(b, a);
}
// lca的准备动作
bfs();
//读入附加边
for (int i = 0; i < m; i++) {
scanf("%d %d", &a, &b);
//树上差分
// dlt[a]的含义：从a->fa这边条，多了一个环
// dlt[b]的含义：从b->fb这边条，多了一个环
dlt[a]++, dlt[b]++;
int p = lca(a, b);
/*
Q:lca(a,b)为什么要减2？
A:边差分，每条边是下放到下面的那个点上，用点来表示这个边的。
其实，每个点表示的是它向上那条边被覆盖的次数，对于lca(a,b)而言，由于dfs统计进行前缀和汇总时，
是左子树+右子树这样的形式进行汇总的，也按同样逻辑处理就会多出2个，需要扣除掉。
*/
dlt[p] -= 2;
}
//差分数组求前缀和
dfs(1, 0);
// Q:为什么要从2开始？
// A:因为1是根，1是没有边的，边是向上的，从2开始才有边
for (int i = 2; i <= n; i++) {
if (dlt[i] == 0) ans += m;
if (dlt[i] == 1) ans += 1;
}
//输出
printf("%d\n", ans);
return 0;
}
