AcWing 356 次小生成树
\(AcWing\) \(356\) 次小生成树
一、分析
本题要求 严格次小生成树，之前在\(AcWing\) \(1148\) 秘密的牛奶运输 里也曾求过次小生成树，但是本题的 数据范围更大 。
本题目因\(N=1e5\),值太大，无法使用 \(AcWing\) \(1148\). 秘密的牛奶运输 的办法（开二维数组，记录\(x->y\)间的 最大边权 和 次大边权），直接报错
additional relocation overflows omitted from the output\(MLE\)了。
void dfs(int s, int u, int fa, int m1, int m2) {
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
int t1 = m1, t2 = m2;
if (w[i] > t1)
t2 = t1, t1 = w[i];
else if (w[i] < t1 && w[i] > t2)
t2 = w[i];
d1[s][j] = t1, d2[s][j] = t2;
dfs(s, j, u, t1, t2);
}
}
for (int i = 1; i <= n; i++)
dfs(i, i, -1, -1e9, -1e9);
也就是说，原来的那个\(dfs+kruskal\)求严格次小生成树的办法，时间复杂度\(TLE\)，空间\(MLE\)，需要一个更牛\(x\)的 求严格次小生成树的办法 了。
秘密的牛奶运输的的性能为什么可以优化呢？这是因为每次执行\(dfs\)求最小生成树上两点路径中的最大边权和次大边权 的时间复杂度是\(O(n)\)，总的时间复杂度就是\(O(n^2)\)，求任意两点间的最短距离可以想办法优化
\(LCA\)树上倍增法申请出战
因为树上倍增法可以求出树上任意两点间的最短距离，扩展一下也可以求也次短距离，而且是\(O(log_2N)\)级别的，比上面的\(O(n)\)快。也就是说本题总的解题流程与秘密的牛奶运输那题基本一致，只是在求 最大边权、次大边权 的方法上有所不同。
二、思路
设\(d[i][k]\)表示树上的某节点\(i\)向上走\(2^k\)步到达的节点，则状态转移方程为
设\(j = d[i][k-1]\)，则状态转移方程表示为
直观的理解就是要想到达离\(i\)距离为\(2^k\)的节点，只需要先走\(2^{k-1}\)步到达\(j\)节点，再从\(j\)节点走\(2^{k-1}\)步就到达了目的节点。
设\(f[i][k]\)表示\(i\)到\(d[i][k]\)节点路径上的最大边权、次大边权，显然
也就是\(i\)到\(d[i][k]\)一共有\(2^k\)条边，边权的 最大值 是\(i\)到\(j\)中边权的 最大值 与\(j\)到\(d[i][k]\)中边权的 最大值 中的 较大者。
\(f[i][k].second\)的求解就需要分情况讨论了：
①if(f[i][k-1].first == f[j][k-1].first)
②f[i][k-1].first > f[j][k-1].first
③f[i][k-1].first < f[j][k-1].first
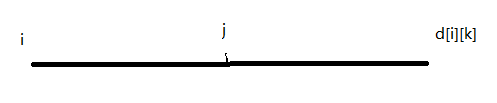
求出了树上任意一点向上走\(2^k\)步路径中的最大边权和次大边权并不是求解本题的终点 ，我们需要的是求解树上任意两点间的最大边权和次大边权。
回忆下求节点\(a\)和节点\(b\)的\(LCA\)的过程，我们先将深度较大的\(a\)节点不断向上跳，直到跳到与\(b\)节点同一深度为止，如果此时\(a\)与\(b\)不重合，则继续将\(a\)和\(b\)以同样的步数向上跳，直到\(a\)和\(b\)的父节点是同一个为止。
求\(LCA\)的树上倍增的过程也可以用来求最大和次大边权，只需要在跳的过程中同步更新最大边权和次大边权即可。
使用 树上倍增法求解树上两点路径中的最大边权和次大边权的时间复杂度降低到了\(O（log_2N）\)，只需要再加上图和树的存储代码以及\(kruskal\)算法的并查集代码就可以了，总的代码如下：
三、实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 100010, M = 300010;
const int INF = 0x3f3f3f3f;
int f[N][16]; // f[i][k]表示树上的某节点i向上走2^k步到达的节点
PII d[N][16]; // d[i][k]表示树上的某节点i向上走2^k步到达的节点最长距离和次长距离
int depth[N]; // 深度数组
// Kruskal用的结构体
struct Edge {
int a, b, c; //从a到b边权为c
bool flag; //是不是最小生成树的树边
const bool operator<(const Edge &ed) const {
return c < ed.c;
}
} edge[M];
//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
//并查集
int p[N];
int find(int x) {
if (x == p[x]) return x;
return p[x] = find(p[x]);
}
//树上倍增求任意两点最短距离
int bfs(int root) {
queue<int> q;
q.push(root);
depth[root] = 1;
while (q.size()) {
int u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!depth[j]) {
depth[j] = depth[u] + 1; //记录深度
q.push(j);
f[j][0] = u; //记录2^0->t,描述父节点
//-->下面是与普通的倍增不一样的代码<--
d[j][0] = {w[i], -INF}; // j->t 的最大距离与次大距离,递推初始化数据
for (int k = 1; k <= 15; k++) { //倍增
int v = f[j][k - 1]; // 设j跳2 ^(k-1)到达的是v点
f[j][k] = f[v][k - 1]; // v点跳2^(k-1)到达的终点就是j跳2^k的终点
//-->下面是与普通的倍增不一样的代码<--
//①最大边权
d[j][k].first = max(d[j][k - 1].first, d[v][k - 1].first);
//②次大边权
if (d[j][k - 1].first == d[v][k - 1].first)
d[j][k].second = max(d[j][k - 1].second, d[v][k - 1].second);
else if (d[j][k - 1].first < d[v][k - 1].first)
d[j][k].second = max(d[j][k - 1].first, d[v][k - 1].second);
else
d[j][k].second = max(d[j][k - 1].second, d[v][k - 1].first);
}
}
}
}
}
//因为同时需要同步修改最大值和次大值，所以采用了地址符&引用方式定义参数
// m1:最大值，m2：次大值
void update(int &m1, int &m2, PII x) {
if (m1 == x.first)
m2 = max(m2, x.second);
else if (m1 < x.first)
m2 = max(m1, x.second), m1 = x.first;
else
m2 = max(m2, x.first);
}
// 最近公共祖先
// 由a->b的边,边权是c
// 返回值：如果加上这条边c，去掉最小生成树中的某条边(m1或m2)，得到一个待选的次小生成树
// 此时的 c- m1 或者 c-m2的值是多少。
// 具体是-m1,还是-m2，要区别对待，因为如果c=m1,就是-m2,否则就是-m1
// 利用倍增的思想，对bfs已经打好的表 d数组和f数组 进行快速查询
// 找出a->b之间的最大距离和次大距离
int lca(int a, int b, int c) {
if (depth[a] < depth[b]) swap(a, b); //保证a的深度大于b的深度
int m1 = -INF, m2 = -INF; //最大边，次大边初始化
for (int k = 15; k >= 0; k--) //由小到大尝试
if (depth[f[a][k]] >= depth[b]) { //让a向上跳2^k步
update(m1, m2, d[a][k]); //可达即可改,先更再前进。
a = f[a][k]; //标准的lca
}
//当a与b不是同一个点时
//此时两者必然是depth一样的情况，同时向上查询2^k，必然可以找到LCA
if (a != b) {
for (int k = 15; k >= 0; k--)
if (f[a][k] != f[b][k]) {
update(m1, m2, d[a][k]);
update(m1, m2, d[b][k]); //可达即可改,先更再前进。注意写在a=f[a][k],b=f[b][k]上方，要不a,b就被改了，此句就不对了
a = f[a][k], b = f[b][k];
}
// 此时a和b到lca下同一层 所以还要各跳1步=跳2^0步
// 联想一下在普通版本LCA中的最终返回值就明白了
// return f[a][0];
update(m1, m2, d[a][0]);
update(m1, m2, d[b][0]);
}
// m1,m2中装的是 a->b之间的最大边权和次大边权，现在给了一个新边权c,它能替换m1,m2,还是谁也替换不了呢？
// 因为m1,m2是最小生成树中的最大边权和次大边权，c >= m1 > m2
// if(c==m1) 那么c能去替换m2,获取的收益就是c-m2
// if(c> m1) 那么c能去替换m1,获取的收益就是c-m1
return c == m1 ? c - m2 : c - m1;
}
int main() {
int n, m, a, b, c;
scanf("%d %d", &n, &m);
//并查集初始化
for (int i = 1; i <= n; i++) p[i] = i;
//邻接表初始化
memset(h, -1, sizeof h);
// Kruskal
for (int i = 0; i < m; i++) {
scanf("%d %d %d", &a, &b, &c);
edge[i] = {a, b, c, 0};
}
//按边权排序+最小生成树
sort(edge, edge + m);
LL sum = 0, ans = 1e18;
for (int i = 0; i < m; i++) {
a = find(edge[i].a), b = find(edge[i].b), c = edge[i].c;
if (a != b) {
p[a] = b;
sum += c; //最小生成树的边权总和
edge[i].flag = true; //标识为最小生成树中的边
//将最小生成树中的树边单独构建一个图出来
add(edge[i].a, edge[i].b, c), add(edge[i].b, edge[i].a, c);
}
}
//倍增预处理,记录任意点向上2^k步的最大值，次大值，深度等信息，后面lca会用到
//以任意点为根
bfs(1);
//用非树边去尝试替换最小生成树中的边，然后取min
// lca查表
for (int i = 0; i < m; i++)
if (!edge[i].flag) { //枚举非树边
a = edge[i].a, b = edge[i].b, c = edge[i].c;
ans = min(ans, sum + lca(a, b, c));
}
//输出
printf("%lld\n", ans);
return 0;
}
