矩阵乘法详解
首先要知道矩阵是怎么相乘的
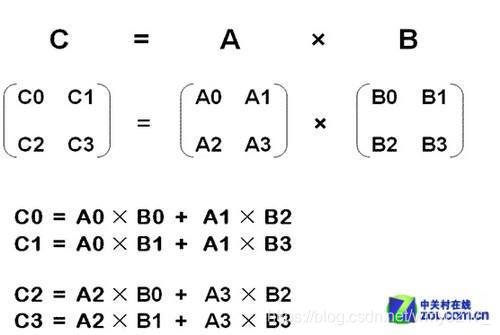
首先，两个矩阵要是想相乘需要满足，第一个矩阵的列数等于第二个矩阵的行数
满足的话就可以相乘得到新的矩阵了。
举个例子嗷：
矩阵\(a\)：
1 2 3
3 2 2
2 1 2
矩阵\(b\)：
2 2
3 1
2 1
\(a\)矩阵是\(3 * 3\)（\(3\)行\(3\)列）的矩阵，\(b\)矩阵是\(3 * 2\)（\(3\)行\(2\)列）的矩阵，满足第一个矩阵的列数等于第二个矩阵的行数。那我们就可以相乘了
一个\(m*n\)的矩阵和一个\(n*p\)的矩阵相乘，将会得到一个\(m*p\)的矩阵
相乘得到的矩阵\(c\)是\(3*2\)的：
14 7
16 10
11 7
其实就是矩阵\(a\)的第一行每个元素分别与\(b\)的第一列相乘再求和，得到\(c\)矩阵的第一个数，然后\(a\)矩阵的第一行再与\(b\)矩阵的第二列相乘，得到第二个数，然后是\(a\)矩阵的第二行与\(b\)矩阵的第一列…
不明白的看下边吧：
1 * 2 + 2 * 3 + 3 * 2 = 14
1 * 2 + 2 * 1 + 3 * 1 = 7
3 * 2 + 2 * 3 + 2 * 2 = 16
3 * 2 + 2 * 1 + 2 * 1 = 10
2 * 2 + 1 * 3 + 2 * 2 = 11
2 * 2 + 1 * 1 + 2 * 1 = 7
好了，懂了怎么相乘就来看题吧…
先看这道题…
题目描述
矩阵\(A\)规模是\(n×m\)，矩阵\(B\)规模是\(m×p\)，现在需要你求\(A*B\)
输入
输入\(n,m\)。然后输入\(n×m\)的矩阵。
输入\(p\),然后输入\(m×p\)的矩阵。
\(1<=n,m,p<=100\)
\(-10000<=\)矩阵元素\(<=10000\)
输出
输出相乘后的\(n×p\)的矩阵
样例输入
2 3
1 2 3
3 2 1
2
1 1
2 2
3 3
样例输出
14 14
10 10
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N][N], b[N][N], c[N][N];
int n, m, p;
int main() {
cin >> n >> m; //矩阵a为n*m（n行m列）
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> a[i][j];
cin >> p; //矩阵b为m*p（m行p列）
for (int i = 0; i < m; i++)
for (int j = 0; j < p; j++)
cin >> b[i][j];
//结果是n行p列的，所以外面两层循环是n和p
//最后一层循环是m，因为(n,m),(m,p),所以(i,k)一组，(k,j)一组
for (int i = 0; i < n; i++) //矩阵c是a与b相乘得到的
for (int j = 0; j < p; j++) // n*p（n行p列）
for (int k = 0; k < m; k++)
c[i][j] += a[i][k] * b[k][j]; //乘法再sum求和
//输出
for (int i = 0; i < n; i++) {
for (int j = 0; j < p; j++)
cout << c[i][j] << " ";
cout << endl;
}
return 0;
}
这一题根上面那一道没什么区别…
L1-048 矩阵\(A\)乘以\(B\)
给定两个矩阵\(A\)和\(B\)，要求你计算它们的乘积矩阵\(AB\)。需要注意的是，只有规模匹配的矩阵才可以相乘。即若\(A\)有\(R_a\)行、\(C_a\)列，\(B\)有\(R_b\)行、\(C_b\) 列，有\(C_a\)与\(R_b\) 相等时，两个矩阵才能相乘。
输入格式：
输入先后给出两个矩阵\(A\)和\(B\)。对于每个矩阵，首先在一行中给出其行数\(R\)和列数\(C\)，随后\(R\)行，每行给出\(C\)个整数，以\(1\)个空格分隔，且行首尾没有多余的空格。输入保证两个矩阵的\(R\)和\(C\)都是正数，并且所有整数的绝对值不超过\(100\)。
输出格式：
若输入的两个矩阵的规模是匹配的，则按照输入的格式输出乘积矩阵\(AB\)，否则输出Error: C_a != R_b，其中\(C_a\)是\(A\)的列数，\(R_b\)是\(B\)的行数。
输入样例1：
2 3
1 2 3
4 5 6
3 4
7 8 9 0
-1 -2 -3 -4
5 6 7 8
输出样例1：
2 4
20 22 24 16
53 58 63 28
输入样例2：
3 2
38 26
43 -5
0 17
3 2
-11 57
99 68
81 72
输出样例2：
Error: 2 != 3
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int a[N][N], b[N][N], c[N][N];
int n, m, p, q;
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> a[i][j];
cin >> p >> q;
for (int i = 0; i < p; i++)
for (int j = 0; j < q; j++)
cin >> b[i][j];
if (m != p)
cout << "Error: " << m << " != " << p;
else {
cout << n << " " << q << endl;
for (int i = 0; i < n; i++)
for (int j = 0; j < q; j++)
for (int k = 0; k < m; k++)
c[i][j] += a[i][k] * b[k][j];
for (int i = 0; i < n; i++) {
for (int j = 0; j < q; j++) {
if (j == q - 1)
cout << c[i][j]; //注意每行最后一个数字后没有空格
else
cout << c[i][j] << " ";
}
if (i != n - 1)
cout << endl;
}
}
return 0;
}
矩阵乘法是一种巧妙地方式将加法转化成乘法的方式，以便在较短的方式解决递推问题。
对于这种加法形递推式，一般都可以使用矩阵乘法加速递推。
矩阵乘法满足结合律，不满足一般的交换律。
利用结合律，矩阵乘法可以利用 快速幂 的思想来优化。
在比赛中，由于线性递推式可以表示成矩阵乘法的形式，也通常用矩阵快速幂来求线性递推数列的某一项。
