A*与IDA* 算法介绍

一、理清概念

• $A*$是对于$bfs$的优化，启发式搜索

• $IDA*$是对于$dfs$的优化，是基于迭代加深的$A*$算法

二、估价函数

$$f = g + h$$

$A*$ 与 $IDA*$ 都是用来搜索路径的算法。它们分别是单纯的$BFS$和$DFS$的优化，其核心都在于对从现状态到目标状态的步数的估计。
即下面这个等式：
$f′ = g′ + h′$

其中$g'$为从初始状态到现状态需要的最少步数，$h′$为从现状态到目标状态需要的最少步数。那么根据等式含义，$f′$就是从初始状态到目标状态，一定要经过现状态时的最少步数。

很显然的是，$f′$ , $g′$ , $h′$都太过理想，是我们不知道的。因此，我们用它们的估算的结果代替使用，即下面这个式子：

$$f = g + h$$

其中$g$为从初始状态到现状态已经走过了多少步，$h$为从现状态到目标状态最少可能会走多少步。

由定义，$g ≥ g′$ ， $f≤f′$ 。（不好理解的话，仔细读定义体会一下。）

下面举个例子（不要纠结例子的合理性啦w）：

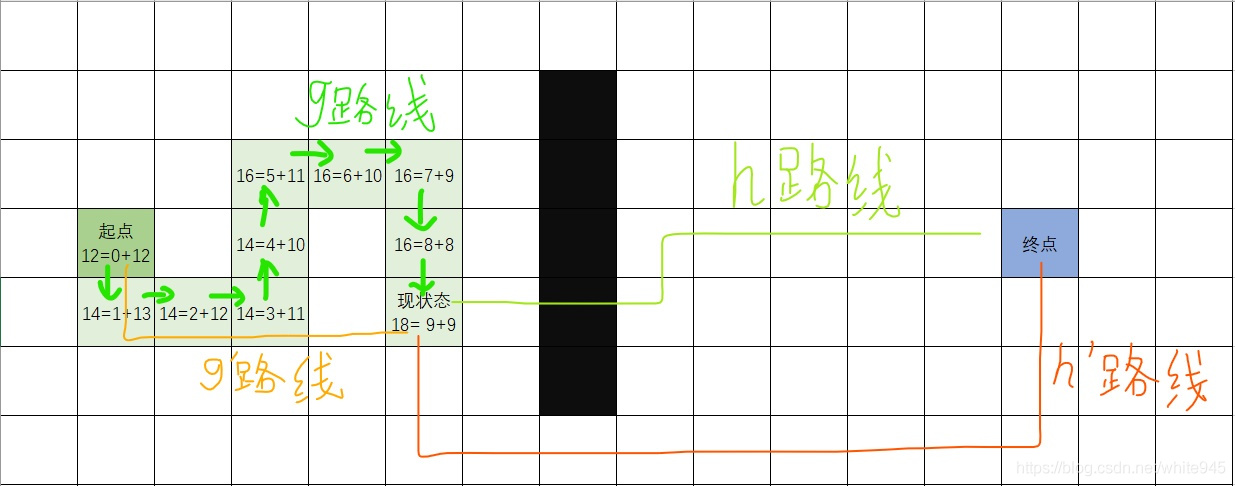
图1

如图一所示，深绿色方块是起点，蓝色方块是终点，黑色是不能经过的部分，浅绿色是本次$dfs$(就当是$dfs$了)的路线，路线中的等式表示$f = g + h$；两条绿色路线分别表示现状态的$g$路线和一条$h$路线，两条橙色路线分别表示现状态的一条$g′$路线和一条$h′$路线（之所以说“一条”，是因为路线不唯一）。可以看出，每次只能从本格子前往上下左右四个格子之一。
现状态：$g = 9，h = 9，g′=5，h′ = 13$。

例子结束。

那么$f = g + h$这个式子是怎么优化$BFS$和$DFS$的呢？请往下看。

三、A*

即优化了的$BFS$。
（安利一个讲得很好的博客：$A*$寻路算法。当然也可以只看我的，十分欢迎。）

$BFS$是一层一层扩展的，也就是我们有目前已经在第$i$步的所有状态，之后由它们拓展出所有第$i+1$步的状态。

很容易想到，当前的所有状态是有优劣之分的，也就是有的状态很可能是正解的必经状态，而有的状态则与正解差了十万八千里。如果我们优先拓展最优的状态，那么就会更快地接近目标。而状态优劣的判断标准显然可以是$f$。

$BFS$通常使用队列实现的。那么这时，我们就可以用优先队列进行优化，以$f$的大小作为判断标准，优先拓展$f$小的。

这，就是$A*$了。

四、IDA*

即优化了的$DFS$。
普通的$DFS$ 不撞南墙不回头，不限制的话，很可能沿着一个错误的方向一直递归下去。而$IDA*$主要有两点升级：

迭代加深
枚举答案的步数。也就是从最小的可能的步数开始往大枚举，直到在这个步数时能从初始状态抵达目标状态。可以简单想一下，每次步数（或者叫深度）加$1$，那么增加的状态数是相当多的，因此可以忽略前面根本抵达不了终点的步数的耗时。

利用$f = g + h$预判是否可能在规定步数抵达终点。假设我们预先设置的步数为$x$，可以知道现状态的$f$，那么如果$f > x$，则现状态到不了终点。
这两点优化都很容易理解，也比较好实现，只要在$dfs$外加一个循环，在$dfs$中加一个提前return的判断语句即可。

如果要输出具体路径的话，$IDA*$在适合不过了。（也不一定啊）最起码回溯时路径就在那里摆着呢啊

这就是 $$IDA*$$ 了。

五、总结

从A和IDA的原理上，我们可以看出它们的核心就是$f = g + h$。$g$是已知的步数，只有$h$是我们需要思考如何求的。$h$的计算方法就因题而异了，不过它一定有以下的性质：

$h$是从现状态到达目标状态的可能的最小步数，也就是说它不一定是真正的最小步数。真正的最小步数是$h′$，是存在，但我们很难求出来的。$h ≤ h′$。$h$越接近$h′$越好。

正是$h$让我们有了预判的能力。$h$函数的定义对一道题有着决定性影响。令$h = 0$，这就是普通的$BFS$和$DFS$了。
$h$真是一个神奇的字母，你$h$了吗?

六、练习题

没有经过细选，只是我遇到的几个例题：
Eight POJ - 1077（这题解法貌似有很多，我用的是IDA）
The Rotation Game POJ - 2286（据说是IDA入门题，TM我用BFS做了一天！！！这也是我开始接触IDA*的题）
[SCOI2005]骑士精神