AcWing 166. 数独

\(AcWing\) \(166\). 数独

一、题目描述

数独 是一种传统益智游戏，你需要把一个 \(9×9\) 的数独补充完整，使得数独中每行、每列、每个 \(3×3\) 的九宫格内数字 \(1\)∼\(9\) 均恰好出现一次。

请编写一个程序填写数独。

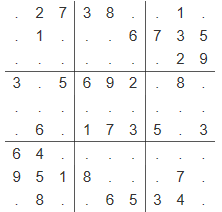
输入格式
输入包含多组测试用例。

每个测试用例占一行，包含 \(81\) 个字符，代表数独的 \(81\) 个格内数据（顺序总体由上到下，同行由左到右）。

每个字符都是一个数字（\(1−9\)）或一个 \(.\)（表示尚未填充）。

您可以假设输入中的每个谜题都只有一个解决方案。

文件结尾处为包含单词 \(end\) 的单行，表示输入结束。

输出格式
每个测试用例，输出一行数据，代表填充完全后的数独。

输入样例：

4.....8.5.3..........7......2.....6.....8.4......1.......6.3.7.5..2.....1.4......
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end

输出样例：

417369825632158947958724316825437169791586432346912758289643571573291684164875293
416837529982465371735129468571298643293746185864351297647913852359682714128574936

二、状态压缩+暴搜

首先介绍普通的 暴搜，就是 自左而右，自上而下的去填充数字 ，直到找到最优解为止。

状态压缩

要想在某个位置上填充x，就需要判断x在 同一行 、 同一列 以及 同一个九宫格 是否出现过。

令r[i]表示第i行的状态，r[i] = 100010001表示第i行 数字 1，5，9已经被填充上了，如果想在第i行的某个空位上填充k，需要判断r[i] >> k & 1是否为0，只有r[i]的第k位是0才可以填充，当然，还需要用c[i]表示第i列的状态。

解释：r[i] >> k & 1 ==1表示数字\(k\)已在同行被使用过了

一共有9个九宫格，也用0-8去编号下，再用w[i]表示第i个九宫格的状态。只要k在 同一行、同一列、同一个九宫格 都没有出现过，就可以去填充了。

这里实现的细节要注意，为了方便，读入时比如第0行填充了3，我们需要写成r[0] += 1 << 3；就算1-9全部填满，也只是把二进制的1-9位全部置为了1，而第0位我们不用去管它，也就是说，实际上我们是维护一个宽度为10的二进制数，然后只去考虑第1-9位上的数是否为1。

\(dfs\)的过程

找到一个空位，枚举1-9，当这个数 不曾出现 在 同一行、同一列、同一九宫格 的时候就填充这个数，并且把该行、该列、该九宫格这个数对应的二进制位置设置为1，然后遍历 下一个位置，遍历完后也要 恢复 所有 全局数组的状态

另外，由于每个数独的答案可能不唯一，找到其中一个就可以返回，不用继续\(dfs\)了。如果只有单个输入，找到解后直接exit(0)即可，但是本题是多组用例，所以为了让\(dfs\)尽快返回，让递归栈里的内容快速弹出，这里在找到最优解后设置一个标志变量flag的值为true，后面\(dfs\)只要遇见flag是true的情况直接返回即可:

#include <bits/stdc++.h>

using namespace std;

const int N = 10;
int g[N][N]; // 棋盘
// 行，列，九宫格分别用的状态压缩桶
// 索引：行，列，九宫格是0~8的索引
// 内容值：1~9位，状态压缩,0位没有用，不用管它。
int r[N], c[N], w[N];
bool flag; // 是不是搜索到了第一个答案，如果是，则让其它搜索快速返回，剪一下枝

// 返回九宫格的编号
int get(int x, int y) {
    x /= 3, y /= 3;   // 注意两个都是/3，表示是第几个小方块，可以理解为0~8，共9个小方块
    return x * 3 + y; // 通过上面的变换，映射到0~8数字上
}

// x,y这个坐标开始暴搜
// cnt:还有多少个点需要填充
void dfs(int x, int y, int cnt) {
    if (flag) return; // 快速返回，剪枝
    if (cnt == 0) {   // 没有空格子了
        // 输出答案
        for (int i = 0; i < 9; i++)
            for (int j = 0; j < 9; j++)
                cout << g[i][j];
        cout << endl;
        // 修改第一次完成的标识
        flag = true;
        return;
    }

    int nx = x, ny = y + 1;    // 下一个位置,默认是向右
    if (ny == 9) nx++, ny = 0; // 越界了就从下一行开始

    if (g[x][y] == 0) {                // 如果此位置是空白
        int u = get(x, y);             // 这是第几号九宫格
        for (int i = 1; i <= 9; i++) { // 尝试填充1~9
            if (r[x] >> i & 1) continue;
            if (c[y] >> i & 1) continue;
            if (w[u] >> i & 1) continue;
            // 修改状态，修改棋盘
            r[x] += 1 << i, c[y] += 1 << i, w[u] += 1 << i, g[x][y] = i;
            // 尝试下一个位置
            dfs(nx, ny, cnt - 1);
            // 恢复状态
            r[x] -= 1 << i, c[y] -= 1 << i, w[u] -= 1 << i, g[x][y] = 0;
        }
    } else // 如果此位置不是空白，那么就尝试下一个位置
        dfs(nx, ny, cnt);
}
int main() {
    string str; // 输入的棋盘
    while (cin >> str && str[0] != 'e') {
        // 初始化
        memset(g, 0, sizeof g); // 清空地图
        memset(r, 0, sizeof r); // 清空行的标识
        memset(c, 0, sizeof c); // 清空列的标识
        memset(w, 0, sizeof w); // 清空9个小方块的标识
        // 找到第一个方案的停止标识
        flag = false;

        // 记录需要填充的空位数量
        int cnt = 0;
        for (int i = 0; i < str.size(); i++) {
            if (str[i] == '.') {
                cnt++;
                continue;
            }
            // 转换为行列坐标
            int x = i / 9, y = i % 9; // x:行，y:列
            int u = get(x, y);        // 0~8哪个九宫格
            g[x][y] = str[i] - '0';   // 棋盘上放上数字
            r[x] += 1 << g[x][y];     // 本质上是一个状态压缩，用二进制方式描述 x行上 g[x][y]这个数字的占用情况，1表示已使用，0表示未使用
            c[y] += 1 << g[x][y];     // 列也用状态压缩描述
            w[u] += 1 << g[x][y];     // 九宫格也用状态压缩描述
        }
        // 从左上角暴搜,cnt描述还有多少个位置需要搜索，当cnt==0时停止
        dfs(0, 0, cnt);
    }
    return 0;
}

四、\(dfs\) + 优化搜索顺序

上面的代码虽然思路比较简洁，按顺序去\(dfs\)，在本题中却会 超时，当然，如果不是多组测试用例肯定不会超时的，因此，需要进行 剪枝 。首先要注意到按顺序\(dfs\)可能会造成很大的 冗余。

比如说一个数独初始时最后一行除了第一列都已经有数字了，只剩下2可以被填充到第一个位置了。如果是我们人去写数独，肯定是先写这种可以填充的数是唯一的位置，然后再去写其他位置。为什么我们会采取这样的 策略 呢？一开始我们就知道最后一行第一列只能填充2，所以其他行的第一列都不能填2，否则就找不到解了。但是方法一的这种搜索必然会导致，枚举第一行第一列时填个2，此时没有违背数独的规则，然后沿着搜索树中2后面的分支搜索个遍，没找到答案再去改第一行第一列上的数。不止如此，\(dfs\)在枚举第二行、第三行一直到第八行第一列位置上的数时也都会考虑2，这将 耗费大量 的时间。如果我们最先枚举的就是最后一行第一列，先把2填进去，这些冗余都是可以避免的，所以，本题搜索顺序很重要。我们应该优先搜索能填数字少的地方。

方法一中，在枚举（x，y）上能填充的数字时，我们是先看这个数字是否在第x行、第y列、第u个九宫格中出现过，设此时行、列、九宫格的状态分别是r、c和w，也就是说。我们是判断r中第k位是0，c中第k位是0，w中第k位也是0才去填充k的。设st = r | c | w，三个对应位都是0的位置才能够填充，因此只要三种状态或起来的状态st的第k为是0就可以填充了，st状态中有几个0，就代表这个位置可以填几种数，我们需要优先枚举0最少也就是1最多的状态。换而言之，就是要遍历数独中所有的空位，找到这些位置中st状态中1最多的位置优先填充。一个二进制数中有多少个1，可以先预处理出来。前面说过，这里状态表示实际上是用了10位的二进制数，所以将\(2^{10} = 1024\)种状态中1的个数都记录下来即可。统计1的个数用lowbit运算即可，比较简单这里不再赘述了。

预备知识

利用\(lowbit\) 求数字二进制表示中1的个数：

#define lowbit(x) (x & -x) //通常用于获取二进制中最低位的值，即最右边的1的位置。
int count(int x) {
    int cnt = 0;
    while (x) x -= lowbit(x), cnt++;
    return cnt;
}

五、优化解法

本题的时间卡的很死，如果使用\(lowbit\)现用现算，仍然会\(TLE\), 需要进一步使用预处理，将\(0 \sim 2^n\)数字，提前一次性计算完它当中二进制表示有多少个数位是\(1\),这样可以避免重复计算，才能正常\(AC\)本题。

#include <bits/stdc++.h>
using namespace std;
const int N = 10;
const int M = (1 << 10) + 10; // 2^10 个可能出现的数字

int g[N][N]; // 棋盘
// 行，列，九宫格分别用的状态压缩桶
// 索引：行，列，九宫格是0~8的索引
// 内容值：1~9位，状态压缩,0位没有用，不用管它。
int r[N], c[N], w[N];
bool flag;  // 是不是搜索到了第一个答案，如果是，则让其它搜索快速返回，剪一下枝
int one[M]; // 每个0~ 2^10-1 的数字当中，每个数字的二进制表示法中数字1的个数

// 方法1
#define lowbit(x) (x & -x)
int count(int x) {
    int cnt = 0;
    while (x) x -= lowbit(x), cnt++;
    return cnt;
}

// 返回九宫格的编号
int get(int x, int y) {
    x /= 3, y /= 3;   // 注意两个都是/3，表示是第几个小方块，可以理解为0~8，共9个小方块
    return x * 3 + y; // 通过上面的变换，映射到0~8数字上
}

void getPos(int &x, int &y) {
    int res = -1; // 每个位置上，已经占用数字最多的是多少个
    // 每次通过9*9的双重循环，枚举出每次哪个位置上需要尝试的数字数量是最少的
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            if (g[i][j]) continue;      // 如果已经填充过，就不用理
            int u = get(i, j);          // 第几个九宫格
            int t = r[i] | c[j] | w[u]; // 三者并集生成的数字
            if (one[t] > res) {         // 这个数字里面的数字1的个数如果大于当前值，修改之。找到1最多的位置
                res = one[t];           // 更新个数最大值
                x = i, y = j;           // 记录当前的坐标
            }
        }
    }
}

// cnt:还有多少个点需要填充
void dfs(int cnt) {
    if (flag) return; // 快速返回，剪枝
    if (cnt == 0) {   // 没有空格子了
        // 输出答案
        for (int i = 0; i < 9; i++)
            for (int j = 0; j < 9; j++)
                cout << g[i][j];
        cout << endl;
        // 修改第一次完成的标识
        flag = true;
        return;
    }

    int x, y; // 记录当前找到的可能性最少的那个点,nx,ny:坐标，nu:哪个九宫格

    // 查询获取到最合理的位置作为尝试顺序
    getPos(x, y);

    // 这是第几个九宫格
    int u = get(x, y);
    for (int i = 1; i <= 9; i++) {
        if (r[x] >> i & 1) continue; // 如果同行出现过，不能填
        if (c[y] >> i & 1) continue; // 如果同列出现过，不能填
        if (w[u] >> i & 1) continue; // 如果同九宫格出现过，不能填
        // 模拟填入
        r[x] += 1 << i, c[y] += 1 << i, w[u] += 1 << i, g[x][y] = i;
        // 递归下一个位置
        dfs(cnt - 1);
        // 恢复现场
        r[x] -= 1 << i, c[y] -= 1 << i, w[u] -= 1 << i, g[x][y] = 0;
    }
}

int main() {
    // 预处理 0~ 2^N 中每个数字二进制表示中数字1的个数
    for (int i = 0; i < 1 << N; i++) one[i] = count(i);

    string str;
    while (cin >> str && str[0] != 'e') {
        // 全部清空一次，因为有多组测试数据
        memset(g, 0, sizeof g);
        memset(r, 0, sizeof r);
        memset(c, 0, sizeof c);
        memset(w, 0, sizeof w);
        // 当前测试数据，还没有找到第一个合理解
        flag = false;

        int cnt = 0;
        for (int i = 0; i < str.size(); i++) {
            if (str[i] == '.') {
                cnt++;
                continue;
            }
            int x = i / 9, y = i % 9;
            int u = get(x, y);
            g[x][y] = str[i] - '0';
            r[x] += 1 << g[x][y];
            c[y] += 1 << g[x][y];
            w[u] += 1 << g[x][y];
        }
        dfs(cnt);
    }
    return 0;
}