凸包知识介绍

一、凸包的定义

凸包($Convex$ $Hull$)是一个计算几何(图形学)中的概念。

在一个实数向量空间$V$中，对于给定集合$X$，所有包含$X$的凸集的交集$S$被称为$X$的凸包。

X的凸包可以用$X$内所有点($X_1$，...$X_n$)的凸组合来构造.

在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈。

用不严谨的话来讲，给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形，它能包含 点集 中所有的点。

如上图所示，点集中外层的点构成的凸多边形就构成了能够包含所有点的凸包，其中连接相邻顶点构成的边越来越平缓，或者说斜率越来越小构成的一组点叫做上凸壳，而相邻的边，斜率越来越大的一组点叫做下凸壳。

关于斜率，同学们可以认为是直线与横轴在第一象限的夹角，夹角越小，斜率越小，夹角越大，斜率越大，换句话说：斜率越小，越贴近x轴，斜率越大，越贴近y轴。

如图所示，开始只有顶点$A、B$构成的凸包，然后加入第三点$C_1$，显然$BC_1$的斜率是高于$AB$的，因此$AB$，$BC_1$构成了一个下凸壳；
但是如果新加的点不是$C_1$而是$C_2$，$BC_2$的斜率小于$AB$，那么$AB$和$BC2$就不能构成下凸壳了，因为不能作为点集的下边界，不能包含在$AB$下面却在$AC_2$上面的点，(这样就不是凸包，而是凹包了！)

因此，加入$C_2$后，$AC_2$将成为下凸壳新的边界了。对于平面上的三点$A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$，(其中$x_1 < x_2 < x_3,y_1 < y_2 < y_3$),$AB$的斜率小于$BC_1$的斜率才能使得$AB$、$BC_1$形成下凸壳。

二、凸包用途

以本节的三道题为例，写一下我对凸包在此专题中作用的理解：


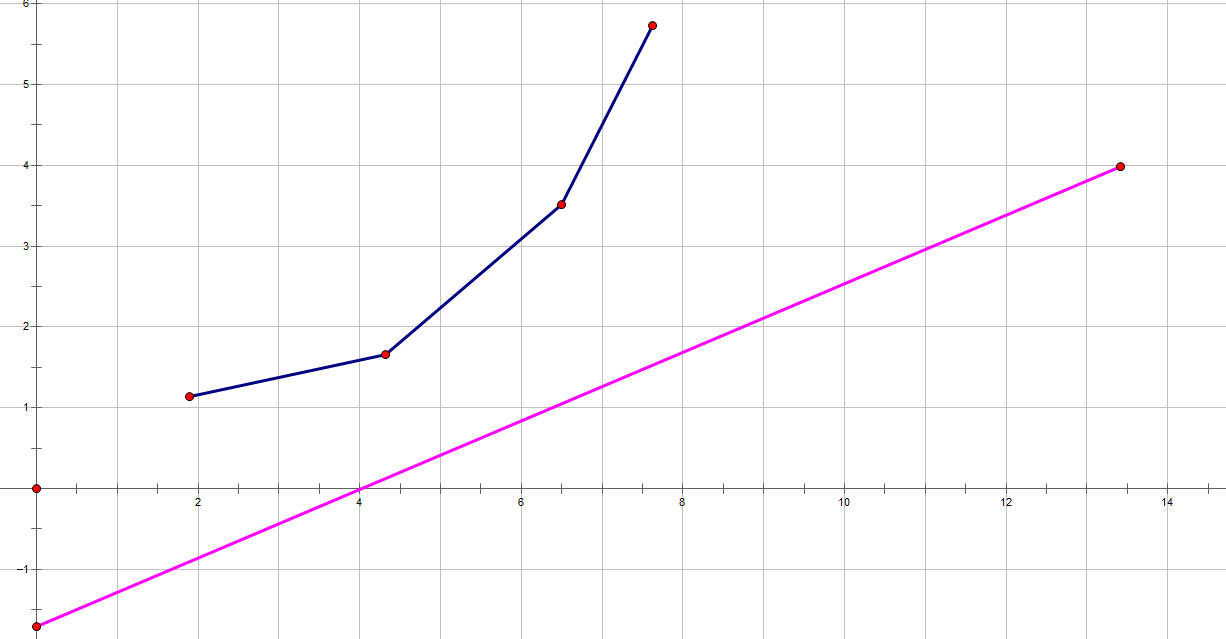
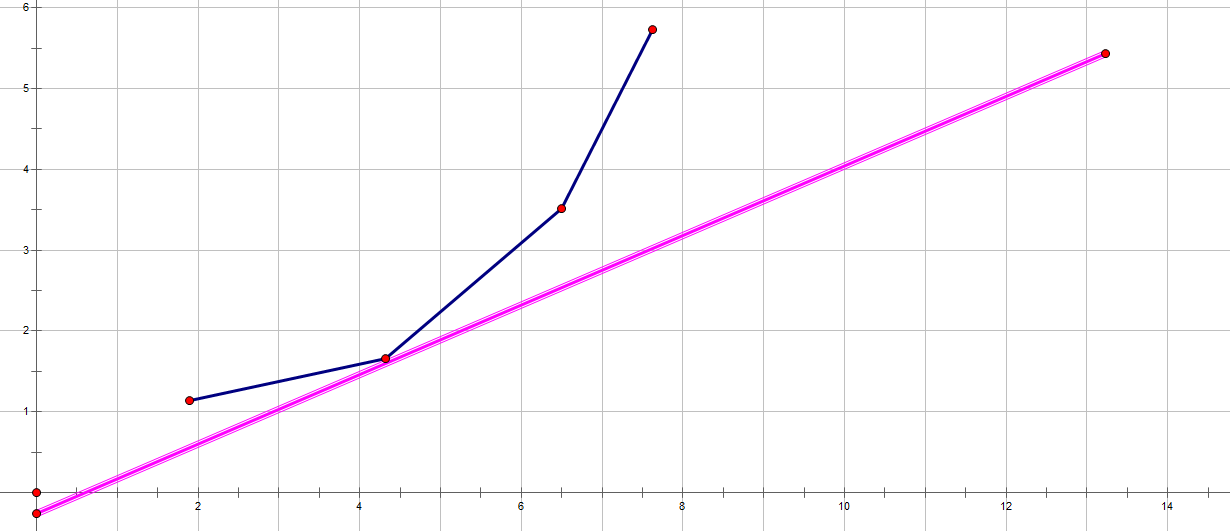
考虑什么时候一个点可以取到最小值

对于点$J_2$，当以$x$为关键字排序后的两个相邻的点$J_1$和$J_3$（在此题中对应$c[j]$的单调性）

当斜率$k_1<k_0<k_2$时，此点就是最优转移点

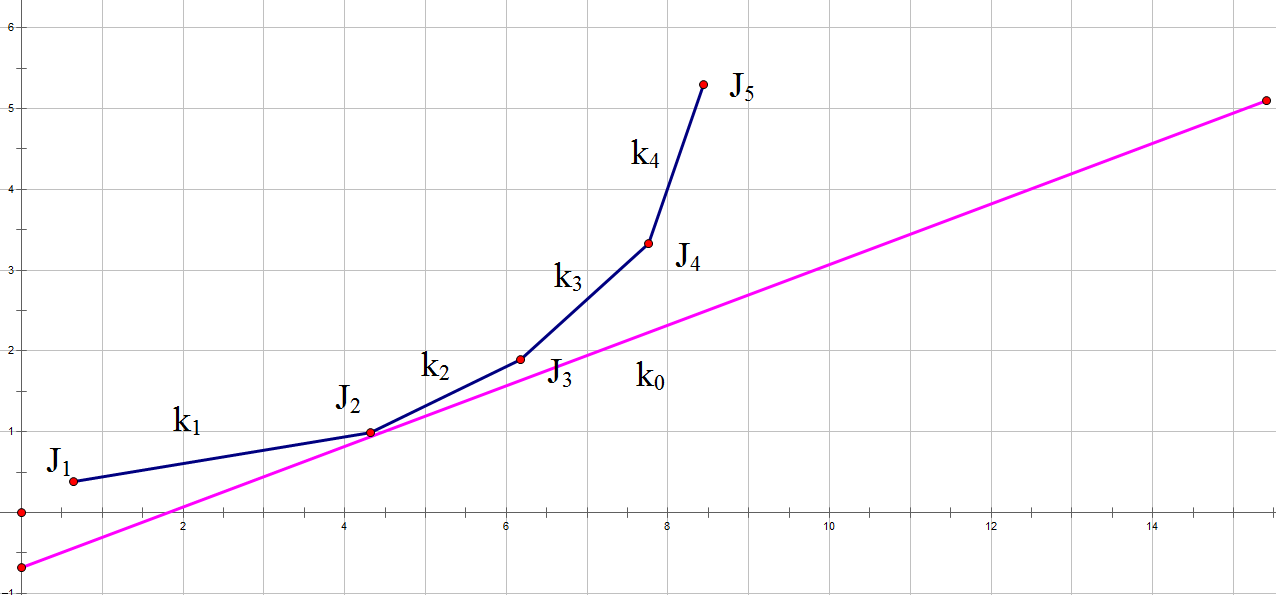
考虑什么时候一个点可能可以取到最小值，什么时候一定不能

如下图，当斜率$k_1<k_2$时，$J_2$是有机会的，此时三个点下凸

当斜率$k_1>=k_2$时，$J_2$不会有一点机会，此时三个点上凸

此处模拟了一条斜率为$k$的直线，上面的点集是它的前序依赖值，问我们，当此直线方程取前序依赖值集中的哪一个点，使得直线方程的截距最小。

答案显而易见，就是从下到上遇到的第一个斜率比自己高的那个点。

非常幸运的是，凸包的维护，也是要求每两个点组成的直线，斜率不断长大，才是下凸壳。换句话说，如果我们用一个单调队列维护了一个下凸壳的话，那么，在这个集合中通过二分查找，很容易能够找到比当前直线斜率高的第一个点，从而求出此直线方程的截距最小值。

整理一下：

1、我们从小到大，不断的向二维空间中增加一些符合直线方程的点，并动态维护好一个凸包（单调队列）。

2、当新的点想要加入时，它需要找出它的前序点中截距最小的点，可以利用二分搜索在凸包队列中快速找出。

3、我们只要维护好凸包，永远都在下凸壳的组成点集中查找，其它点都肯定不是答案，这样明显提速。再加上面2中提到的单调性+二分，速度杠杠滴~