AcWing 135. 最大子序和
\(AcWing\) \(135\). 最大子序和
一、题目描述
输入一个长度为 \(n\) 的整数序列，从中找出一段 长度不超过 \(m\) 的连续子序列，使得子序列中所有数的和最大。
注意： 子序列的长度至少是 \(1\)。
输入格式
第一行输入两个整数 \(n,m\)。
第二行输入 \(n\) 个数，代表长度为 \(n\) 的整数序列。
同一行数之间用空格隔开。
输出格式
输出一个整数，代表该序列的最大子序和。
数据范围
\(1≤n,m≤300000\),保证所有输入和最终结果都在 int 范围内。
输入样例：
6 4
1 -3 5 1 -2 3
输出样例：
7
二、暴力作法
如果只要 固定长度为\(m\)的连续子区间 元素总和最大，那就是个简单的滑动窗口，我们先计算一下前缀和，然后维护一个滑动窗口，一边加来一边减就行了。
此题就难度提升了，因为是一个 长度不超过\(m\) 的连续子区间！
窗口长度不固定，那我们就考虑枚举每个位置做为终点，然后从终点向回走，最长枚举\(m\)个长度，这样纯暴力的思路就出来了！
暴力大法
\(TL\)E掉\(3\)个点
通过了 \(11/14\)个数据
#include <bits/stdc++.h>
using namespace std;
// Brute-force 暴力
const int N = 300010;
const int INF = 0x3f3f3f3f;
int s[N];
int n, m;
// TLE掉3个点,通过了 11/14个数据
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> s[i], s[i] += s[i - 1];
int res = -INF;
// 遍历每一个终点
for (int i = 1; i <= n; i++)
// 从终点向前，找出所有区间在m之内的数字，通过前缀和计算出区间的累加和，保留最大值
// 在刚刚出发不久，长度不够m的时候,即i<m,则i-m会出现负数
for (int j = i; j > max(0, i - m); j--)
res = max(res, s[i] - s[j - 1]); // j>0 && j> i-m --> j> max(0,i-m)
printf("%d\n", res);
return 0;
}
三、优化办法
本题的数据范围是\(30w\)，上面平方级别复杂度的代码显然会超时。
状态表示
\(f[i]\):以第\(i\)个数字结尾的长度不超过\(m\)的子序列的最大和
\(s[i]\):数组的前缀和，则\(a[l] + ... + a[r] = s[r] - s[l-1]\)
状态转移方程为\(f[i] = max(s[i] - s[j-1])\)，其中\(i - j\)大于等于\(0\)并且不超过\(m\)
举个栗子：
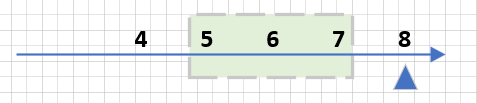
- 假设：现在\(i=8,m=3\),就是要找出包括\(i=8\)在内，\(3\)个数字的窗口中，窗口的最大值:
- 每次计算累加和不好计算，我们采用前缀和优化一下
- 当前枚举到了\(8\),可以认为\(s[8]\)是固定值，那么其实就是在求
这些数字的特点是：\(8\)的左侧三个范围内，前缀和最小。典型的 单调队列求极小值问题。
-
推广到通用形态，当前枚举到的是\(i\),那么就是在求$$\large min(s[i-1],s[i-2],…,s[i-m])$$ (可以类比一下上面的例子)
-
由上面的分析得知，其实这个窗口就是在\(i\)前面的\(m\)个位置内！不包括\(i\)
-
采用单调队列优化一下，可以在\(O(1)\)时间内找出前面\(m\)个数的最小值：维护一个队列，保存距离当前结点前面\(i-1 \sim i-m\)范围内的前缀和最小的那个结点索引下标。每次计算到\(i\)时，直接取队列中的队头进行计算即可。
因为\(i\)不在窗口中，当枚举到\(i\)时，需要在它未加入到队列前查询队列头！ -
考虑一下边界问题，如果\(i=1\)，那么它也需要向队列中去找出它前面的最小前缀和,而它是第一个进来的，还没有来得及维护队列，这样的话就找不到了，需要手动向队列中初始化一个合理的初始化值 【哨兵】。从本题来说，就是第一个数字前面的所有前缀和，当然是\(0\)，即\(q[hh]=q[0]=0,tt++\); 并且因为\(q\)是定义在全局变量区，默认就是\(0\)，不用再写这句，所以直接\(tt=0\)就描述了初始化的过程。
算法细节
在单调队列的实现时，需要先在队列中加入哨兵结点\(s[0]\)，后面就是解决四个问题:
-
① 何时出队头，枚举到第\(i\)个数字时，第\(i\)个数字还没加入队列时，队头元素的下标允许的最小值是\(i - m\)，所以当\(i - q[hh] > m\)时就需要出队头了
-
② 何时出队尾，我们需要队头的元素是\(s[q[hh]]\)最小的元素，所以当\(s[i] <= s[q[tt]]\)时，出队尾元素
-
③ 何时加入新元素，队尾元素该出的出完了就可以将\(i\)加入到队列中了
-
④ 何时更新我们要求的长度不超过\(m\)的子序列的和的最大值\(res\)，只要在确保队列中的元素个数不超过\(m\)时就可以尝试更新\(res\)了
时间复杂度
使用单调队列优化\(DP\)的方法时间复杂度是\(O(n)\)。
四、单调队列实现
#include <bits/stdc++.h>
using namespace std;
const int N = 300010;
const int INF = 0x3f3f3f3f;
int n, m;
int q[N];
// 单调队列，本质记录的是下标序号，因为只有记录了下标，才能知道是否离i的距离长度超过m了没有。
// 同时，记录了下标的话，想要其它的信息都是可以表示出来的，比如s[q[hh]]
int s[N]; // 前缀和
int res = -INF; // 预求最大，先设最小
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> s[i], s[i] += s[i - 1]; // 前缀和
int hh = 0, tt = 0; // 等价于增加了一个哨兵节点,也就是把下标为0的前缀和s[0]=0加入了滑动窗口中，描述1号节点向前m个节点的前缀和最小值是0
// 枚举右边界
for (int i = 1; i <= n; i++) {
// 1、老掉牙的需要去世
while (hh <= tt && q[hh] < i - m) hh++;
// 2、此时单调队列中保存就是i以前、长度最长为m的单调上升的一个序列，队列头保存的就是i前面前缀和的最小值
// 此时i还没有进入队列，单调队列其实在枚举数字i的左侧
res = max(res, s[i] - s[q[hh]]);
/*
把0，也就是sum(0)塞入队列中（这是给sum（1）用的，因为可能sum（1）-sum（0）就是最大的子序列，不加这个0就没法计算了），最小值为0
*/
// 3、i入队列
// 比i老没它小的都去死吧~
while (hh <= tt && s[q[tt]] >= s[i]) tt--;
// i入队列,本轮结束
q[++tt] = i;
}
// 输出结果
cout << res << endl;
return 0;
}
