AcWing 1073. 树的中心
\(AcWing\) \(1073\). 树的中心
一、题目描述
给定一棵树，树中包含 \(n\) 个结点（编号\(1\)~\(n\)）和 \(n−1\) 条无向边，每条边都有一个权值。
请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 \(n\)。
接下来 \(n−1\) 行，每行包含三个整数 \(a_i,b_i,c_i\)，表示点 \(a_i\) 和 \(b_i\)
之间存在一条权值为 \(c_i\) 的边。
输出格式
输出一个整数，表示所求点到树中其他结点的最远距离。
数据范围
\(1≤n≤10000,\)
\(1≤a_i,b_i≤n,\)
\(1≤c_i≤10^5\)
输入样例：
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例：
2
二、暴力大法
国际惯例上来就写暴力:
对每一个点都求得它的 最远距离, 答案=\(min(\)所有点的最远距离\()\)
通过 \(7/11\)个数据然后\(TLE\)
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 10010, M = N << 1;
int n;
int ans;
int res = INF;
// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void dfs(int u, int fa, int sum) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v == fa) continue;
dfs(v, u, sum + w[i]);
}
ans = max(ans, sum);
}
int main() {
memset(h, -1, sizeof h);
cin >> n;
for (int i = 1; i < n; i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
// 暴力换根
for (int i = 1; i <= n; i++) {
ans = 0;
dfs(i, 0, 0);
res = min(res, ans);
}
printf("%d\n", res);
return 0;
}
三、换根\(DP\)【模板，背诵】
注：与前一题类似，也是怕两重循环导致时间复杂度上升到\(O(N^2)\),不能遍历每两个节点，只能是遍历每个节点，尝试构建此节点的上下游信息，再用这些信息找出树的中心。
换根\(DP\)就是根据父亲的属性来更新他更新儿子的属性，相当于只需要考虑把顶点移到儿子对结果造成的影响。
同样，先来想一下如何暴力求解该问题：先 枚举 目标节点，然后求解该节点到其他节点的 最远距离
时间复杂度为 \(O(n^2)\)，对于本题的 数据规模，十分极限，经测试只能过 \(7/11\)
考虑如何优化求解该问题的方法
思考一下：在确定树的 拓扑结构 后单独求一个节点的 最远距离 时，会在该树上去比较哪些 路径 呢？
- 从当前节点往下，直到子树中某个节点的最长路径
- 从当前节点往上走到其父节点，再从其父节点出发且不回到该节点的最长路径
此处就要引入 换根\(DP\) 的思想了
换根\(DP\) 一般分为三个步骤：
- 指定任意一个根节点
- 一次\(dfs\)遍历，统计出当前子树内的节点对当前节点的贡献
- 一次\(dfs\)遍历，统计出当前节点的父节点对当前节点的贡献，然后合并统计答案
那么我们就要先 \(dfs\) 一遍，预处理出当前子树对于根的 最大贡献(距离) 和 次大贡献（距离）
处理 次大贡献（距离） 的原因是：
如果 当前节点 是其 父节点子树 的 最大路径 上的点，则 父节点子树 的 最大贡献 不能算作对该节点的贡献
因为我们的路径是 简单路径，不能 走回头路
然后我们再 \(dfs\) 一遍，求解出每个节点的父节点对他的贡献（即每个节点往上能到的最远路径)
两者比较，取一个 \(max\) 即可
我们用 \(mx1[u],mx2[u],up[u],id[u]\)分别存一下需要的信息，这些数据存的是：
\(mx1[u]\)：存下\(u\)节点向下走的最长路径的长度
\(mx2[u]\)：存下\(u\)节点向下走的第二长的路径的长度
\(id[u]\)：存下\(u\)节点向下走的最长路径是从哪一个节点下去的
\(up[u]\)：存下\(u\)节点向上走的最长路径的长度
图解
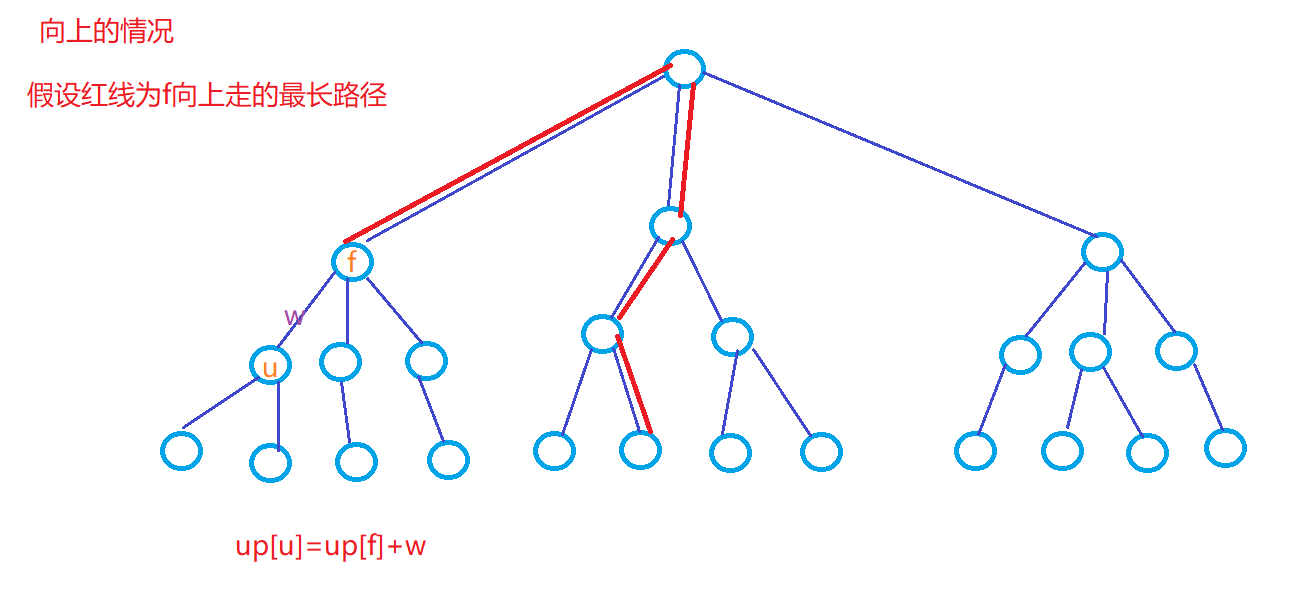
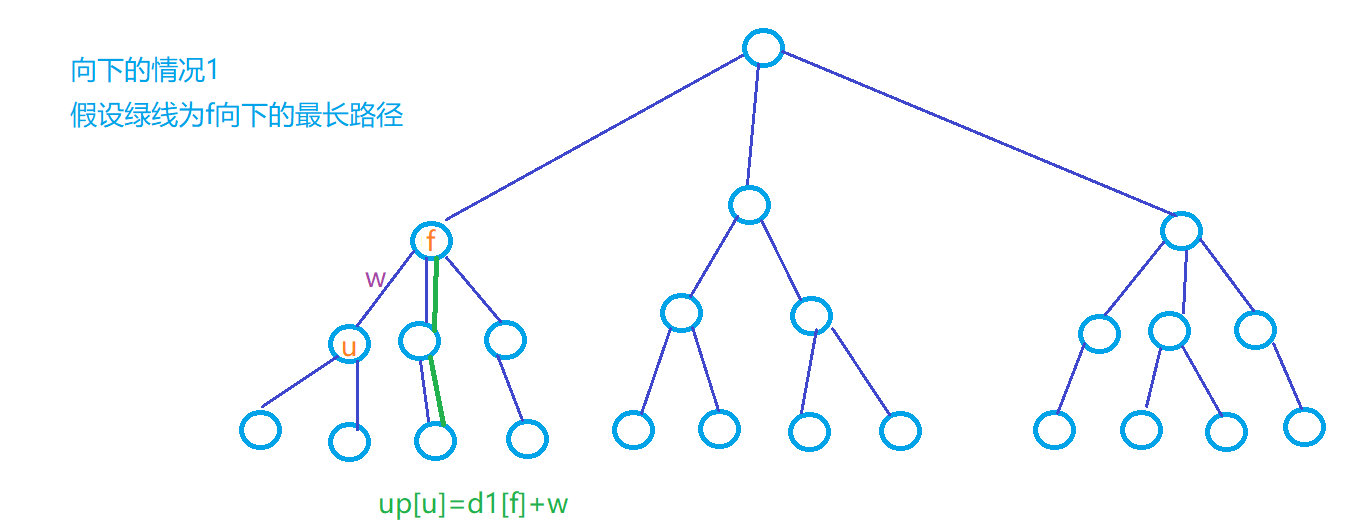
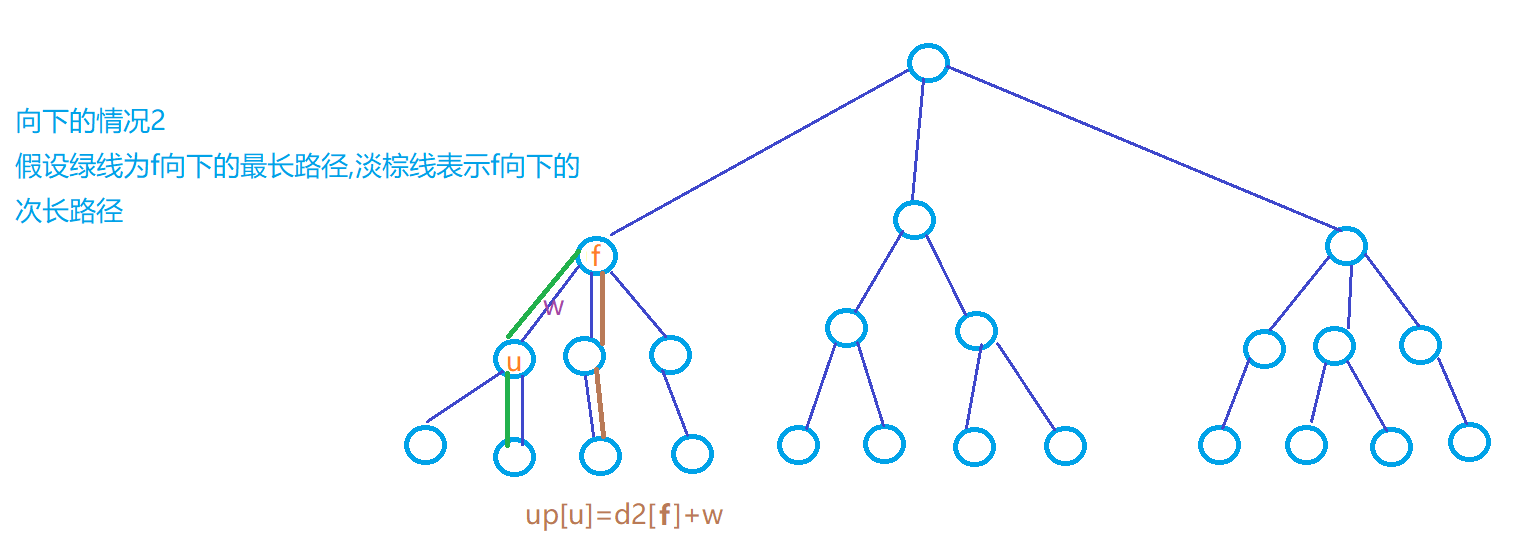
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = N << 1;
const int INF = 0x3f3f3f3f;
int n; // n个节点
int mx1[N]; // mx1[u]：u节点向下走的最长路径的长度
int mx2[N]; // mx2[u]：u节点向下走的次长路径的长度
int id[N]; // id[u]：u节点向下走的最长路径是从哪一个节点下去的
int up[N]; // up[u]：u节点向上走的最长路径的长度
// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 功能:以u为根，向叶子进行递归，利用子节点返回的最长信息，更新自己的最长和次长,并记录最长是从哪个节点来的
void dfs1(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v == fa) continue;
// 递归完才能有数据
dfs1(v, u);
int x = mx1[v] + w[i]; // u问到：儿子v可以带我走多远？
if (mx1[u] < x) { // 更新最长
mx2[u] = mx1[u]; // ① 更新次长
mx1[u] = x; // ② 更新最长
id[u] = v; // ③ 记录最长来源
} else if (mx2[u] < x) // 更新次长
mx2[u] = x;
}
}
// 功能：完成向上的信息填充
void dfs2(int u, int fa) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (v == fa) continue;
// 二者取其一
if (id[u] == v)
up[v] = max(mx2[u], up[u]) + w[i];
else
up[v] = max(mx1[u], up[u]) + w[i];
// 递归
dfs2(v, u);
}
}
int main() {
memset(h, -1, sizeof h);
cin >> n;
for (int i = 1; i < n; i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs1(1, 0); // 选择任意一个节点进行dfs,用儿子更新父亲的统计信息
dfs2(1, 0); // 向上
int res = INF;
for (int i = 1; i <= n; i++) res = min(res, max(mx1[i], up[i]));
printf("%d\n", res);
return 0;
}
