AcWing 8. 二维费用的背包问题
\(AcWing\) \(8\). 二维费用的背包问题
一、题目描述
有 \(N\) 件物品和一个容量是 \(V\) 的背包,背包能承受的最大重量是 \(M\)。
每件物品只能用一次。体积是 \(v_i\),重量是 \(m_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。
输出最大价值。
输入格式
第一行三个整数,\(N,V,M\),用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 \(N\) 行,每行三个整数 \(v_i,m_i,w_i\),用空格隔开,分别表示第 \(i\) 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
\(0<N≤1000,0<V,M≤100,0<v_i,m_i≤100,0<w_i≤1000\)
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例:
8
二、分析
每件物品只能 用一次 因此是个 01背包模型
费用一共有两个,一个是 体积,一个是 重量,因此是个 01背包二维费用问题
本题是一道裸题,直接上 闫氏DP分析法
闫氏DP分析法
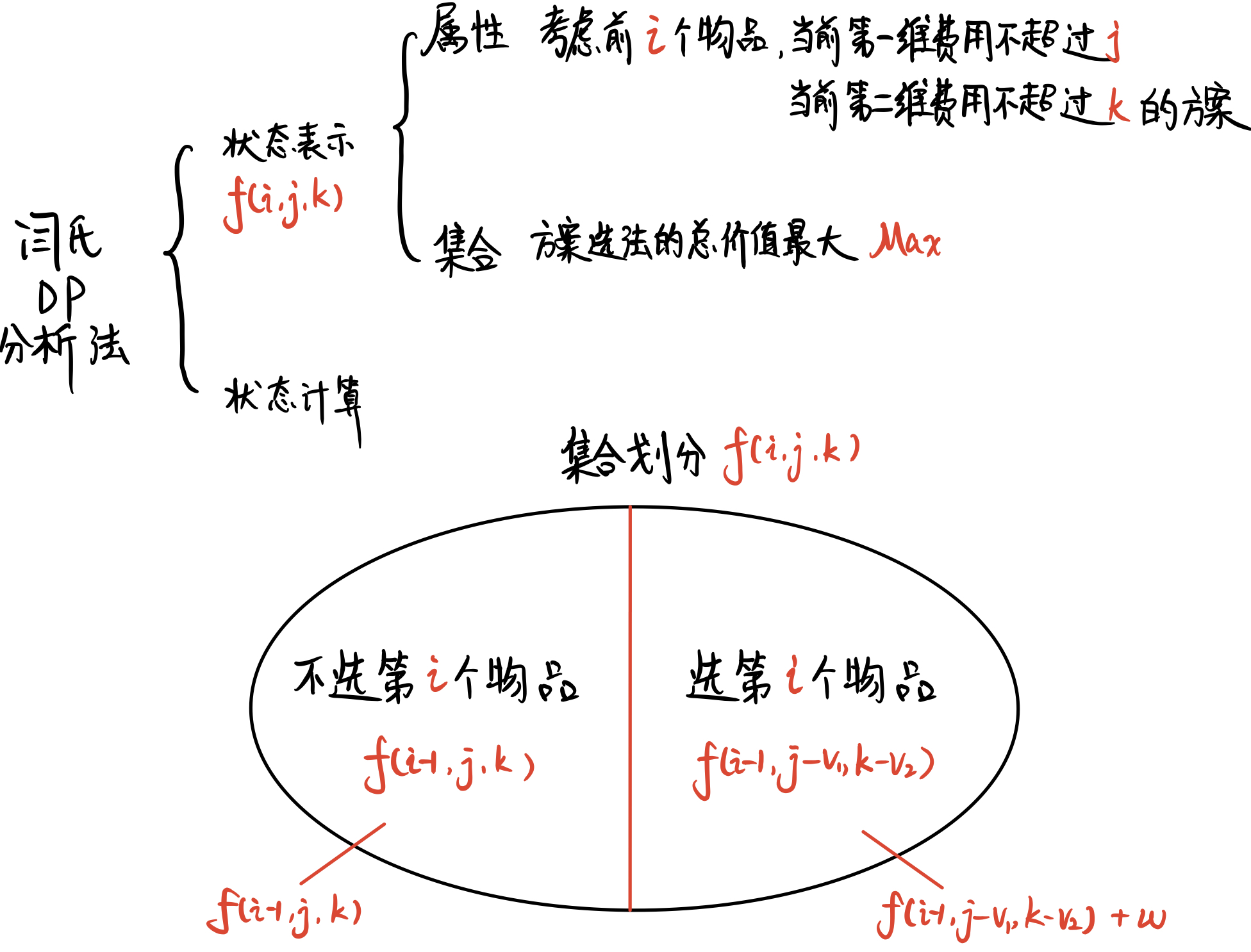
初始状态:f[0][0][0]
目标状态:f[n][V][M]
状态转移方程:
-
当剩余的空间\(j\)不能装下当前物品\(i\),即\(j<v_1\)时不能选择\(i\)物品。
\(f[i,j,k]=f[i−1,j,k]\) -
当剩余的重量\(k\)不能装下当前物品\(i\),即\(k<v_2\)时不有选择\(i\)物品。
\(f[i,j,k]=f[i−1,j,k]\) -
当\(j>=v_1\&\&k>=v_2\)时,可以选择要\(i\),还是不要\(i\)。
- 不要\(i\):\(f[i,j,k]=f[i−1,j,k]\)
- 要\(i\):\(f[i,j,k]=f[i−1,j−v_1,k−v_2]+w\)
三、三维数组解朴素解法
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = 110;
int n;
int m1, m2;
int f[N][M][M];
int main() {
cin >> n >> m1 >> m2;
for (int i = 1; i <= n; i++) {
int v1, v2, w;
cin >> v1 >> v2 >> w;
for (int j = 0; j <= m1; j++)
for (int k = 0; k <= m2; k++) {
f[i][j][k] = f[i - 1][j][k];
if (j >= v1 && k >= v2)
f[i][j][k] = max(f[i - 1][j][k], f[i - 1][j - v1][k - v2] + w);
}
}
printf("%d", f[n][m1][m2]);
return 0;
}
四、二维数组空间优化解法
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = 110;
int n;
int m1, m2;
int f[M][M];
int main() {
cin >> n >> m1 >> m2;
for (int i = 1; i <= n; i++) {
int v1, v2, w;
cin >> v1 >> v2 >> w;
for (int j = m1; j >= v1; j--)
for (int k = m2; k >= v2; k--)
f[j][k] = max(f[j - v1][k - v2] + w, f[j][k]);
}
printf("%d\n", f[m1][m2]);
return 0;
}


