AcWing 1019. 庆功会

\(AcWing\) \(1019\). 庆功会

一、题目描述

为了庆贺班级在校运动会上取得全校第一名成绩，班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。

期望拨款金额能购买最大价值的奖品，可以补充他们的精力和体力。

输入格式
第一行二个数\(n，m\)，其中\(n\)代表希望购买的奖品的种数，\(m\)表示拨款金额。

接下来\(n\)行，每行\(3\)个数，\(v、w、s\)，分别表示第\(I\)种奖品的价格、价值（价格与价值是不同的概念）和能购买的最大数量（买\(0\)件到\(s\)件均可）。

输出格式
一行：一个数，表示此次购买能获得的最大的价值（注意！不是价格）。

数据范围
\(n≤500,m≤6000\),\(v≤100,w≤1000,s≤10\)

输入样例：

5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1

输出样例：

1040

二、题目解析

物品个数为 \(n\)，总体积为\(m\)，初步识别是一个 背包问题

观察到每个物品有 数量限制，断定该题是 多重背包问题

本题是一道 多重背包 的裸题

不多废话，我们直接上 闫氏DP分析法

闫氏DP分析法

初始状态：f[0][0]
目标状态：f[n][m]

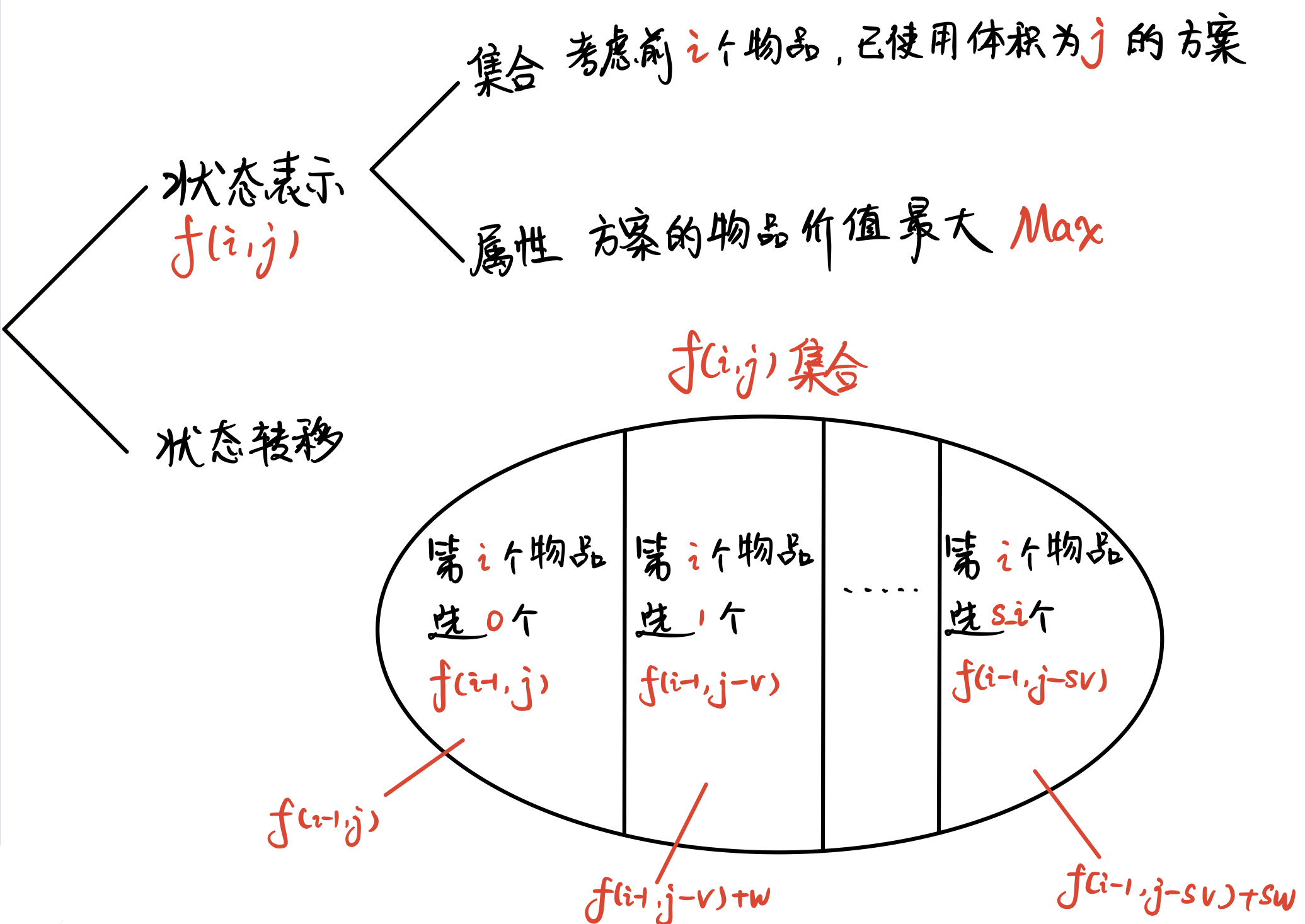
三、朴素版本解法

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 6010;

int n, m;
int v[N], w[N], s[N];
int f[N][M];

// 二维朴素作法
int main() {
    cin >> n >> m;

    for (int i = 1; i <= n; i++) {
        int v, w, s;
        cin >> v >> w >> s;
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= s && j >= k * v; k++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);
    }
    printf("%d\n", f[n][m]);
    return 0;
}