AcWing 6. 多重背包问题 III
AcWing 6. 多重背包问题 III
一、题目描述
有 \(N\) 种物品和一个容量是 \(V\) 的背包。
第 \(i\) 种物品最多有 \(s_i\) 件,每件体积是 \(v_i\),价值是 \(w_i\)。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,\(N,V\) (\(0<N≤1000, 0<V≤20000\)),用空格隔开,分别表示物品种数和背包容积。
接下来有 \(N\) 行,每行三个整数 \(v_i,w_i,s_i\),用空格隔开,分别表示第 \(i\) 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
\(0<N≤1000\)
\(0<V≤20000\)
\(0<v_i,w_i,s_i≤20000\)
提示
本题考查多重背包的单调队列优化方法。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
二、多重背包的前世今生
\(AcWing 4\). 多重背包问题 I
\(AcWing 5\). 多重背包问题 II
\(AcWing 6\). 多重背包问题 III
三、空间问题
下面将讨论此问题的三种解法,特别说明的是,二维最好理解,而且空间范围也是在可以接受的范围内,不必盲目追求一维,性能上不会带来提升。以最终极版本的单调队列优化算法来说,需要的二维空间最大值就是\(f[N][M]\),其中\(N*M=1000\times 20000=20000000\),换算成空间大小就是$$\large 1000\times 20000\times4/1024/1024=76MB$$,一般题目的空间限制都是\(128MB\)左右,再加上\(C++\)程序运行需要的一部分内存,是可以正常通过测试的,事实上二维方法,在
AcWing 6. 多重背包问题 III中,是可以正常\(AC\)的。
即使题目限制了内存大小最多为\(64MB\)(这就很\(BT\)了),也可以简单的使用滚动数组的方法优化,$$\large 2\times 20000\times4/1024/1024=16MB$$,足够过掉此题,一维限制无意义,也不做为讲解的重点,此文只关注二维实现,文末将附上一维实现办法。
四、三种解法
三种解法的根本区别在于数据范围,题面都是一样的:
| ① 朴素版本 | ② 二进制优化版本 | ③ 单调队列优化版本 |
|---|---|---|
| \(n≤100\),\(V≤100\) | \(n≤1000\),\(V≤2000\) | \(n≤1000\),\(V≤20000\) |
-
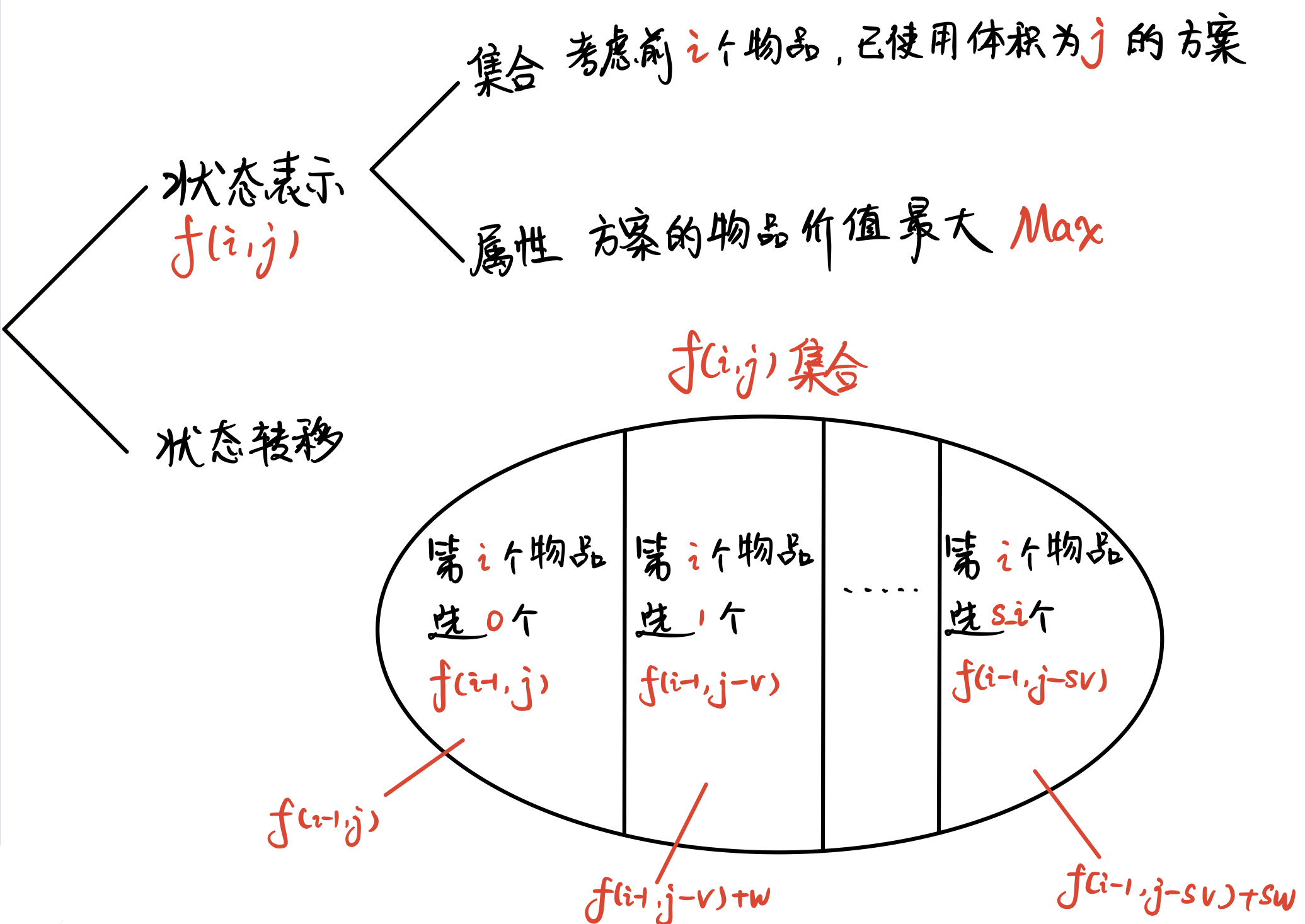
状态表示
集合:所有只从前\(i\)个物品中选,并且总体积不起过\(j\)的选法
属性:集合中每一个选法对应的总价值的最大值 -
状态计算
就是一个集合划分的过程,就是和完全背包很像,但不像完全背包有无穷多个,而是有数量限制 -
初始状态:
f[0][0] -
目标状态:
f[n][m]
状态转移方程
四、朴素算法
二维朴素
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int f[N][N];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
int v, w, s;
scanf("%d %d %d", &v, &w, &s);
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s && v * k <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v] + w * k);
}
printf("%d\n", f[n][m]);
return 0;
}
一维朴素
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int f[N];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
int v, w, s;
scanf("%d %d %d", &v, &w, &s);
for (int j = m; j >= v; j--)
//注意:此处k=0,k=1是一样的
//如果不要i物品 即 f[i][j]=f[i-1][j]
//转为一维表示法,就是f[j]=f[j],所以从0从1都一样
for (int k = 0; k <= s && k * v <= j; k++)
f[j] = max(f[j], f[j - v * k] + w * k);
}
printf("%d\n", f[m]);
return 0;
}
在可以考虑第\(i\)个物品时,前面\(i-1\)个物品已经做出了选择,前面怎么选择的我不管,我只管我现在面临的情况该怎么处理:
\(
\large \left\{\begin{array}{l}
第i个物品一个也不选择 & \\
第i个物品一个选1个& \\
第i个物品一个选2个& \\
... & \\
第i个物品一个选s_i个&
\end{array}\right.
\)
当然,你也不能真的一定从\(0\)选择到\(s_i\)个,因为可能你的背包装不上了,需要加上限制条件:\(v*k<=j\)
五、二进制优化
朴素多重背包做法的本质:将有数量限制的相同物品看成多个不同的\(0-1\)背包。
优化的思路:比如我们从一个货车搬百事可乐的易拉罐(因为我爱喝不健康的快乐水~),如果存在\(200\)个易拉罐,小超市本次要的数量为一个小于\(200\)的数字\(n\),搬的策略是什么呢?
A、一个一个搬,直到\(n\)为止。
B、在出厂前打成\(64\)个一箱,\(32\)个一箱,\(16\)个一箱,\(8\)个一箱,\(4\)个一箱,\(2\)个一箱,\(1\)个一箱,最后剩下的打成\(73\)个一箱。
为什么要把剩下的\(73\)个打成一个包呢?不是再分解成\(64\),\(32\)这样的组合呢?这是因为我们其实本质是化解为\(01\)背包,一来这么分解速度最快,二来可以表示原来数量的任何子集,这样就\(OK\)了!
二维二进制版本
#include <bits/stdc++.h>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[N][M]; //二维数组版本,AcWing 5. 多重背包问题 II 内存限制是64MB
//只能通过滚动数组或者变形版本的一维数组,直接二维数组版本MLE
//多重背包的二进制优化
int main() {
scanf("%d %d", &n, &m);
int idx = 0;
for (int i = 1; i <= n; i++) {
int a, b, s;
scanf("%d %d %d", &a, &b, &s);
//二进制优化,能打包则打包之,1,2,4,8,16,...
int k = 1;
while (k <= s) {
idx++;
v[idx] = a * k;
w[idx] = b * k;
s -= k;
k *= 2;
}
//剩下的
if (s > 0) {
idx++;
v[idx] = a * s;
w[idx] = b * s;
}
}
n = idx; //数量减少啦
// 01背包
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
printf("%d\n", f[n][m]);
return 0;
}
一维数组二进制版本
#include <bits/stdc++.h>
using namespace std;
const int N = 12010, M = 2010;
int n, m;
int v[N], w[N];
int f[M];
//多重背包的二进制优化
int main() {
scanf("%d %d", &n, &m);
int cnt = 0;
for (int i = 1; i <= n; i++) {
int a, b, s;
scanf("%d %d %d", &a, &b, &s);
//二进制优化,能打包则打包之,1,2,4,8,16,...
int k = 1;
while (k <= s) {
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
//剩下的
if (s > 0) {
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt; //数量减少啦
// 01背包
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
六、单调队列优化
使用朴素版本利用数据进行调试,找一下规律,看看哪个状态间存在转移关系:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int v, w, s;
int f[N];
/**
* 测试用例:
2 9
3 5 2
2 4 3
*/
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
cin >> v >> w >> s; //体积、价值、数量
scanf("%d %d %d", &v, &w, &s);
//一维是倒序,而且最小值可以到达v
for (int j = m; j >= v; j--)
for (int k = 0; k <= s && j >= k * v; k++) {
f[j] = max(f[j], f[j - k * v] + k * w);
//输出中间过程,用于调试,找规律
printf("f[%d]=%2d f[%d]+%d=%d\n", j, f[j], j - k * v, k * w, f[j - k * v] + k * w);
}
}
return 0;
}

二维版本
#include <bits/stdc++.h>
using namespace std;
const int N = 1010; // 物品种类上限
const int M = 20010; // 背包容量上限
int n, m;
int f[N][M]; // 前i个物品,在容量为j的限定下,最大的价值总和
int q[M]; // 单调优化的队列
// 二维朴素版+队列[k-s*v,k],队列长s+1
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) { // 枚举每个物品
int v, w, s; // 体积、价值、个数
cin >> v >> w >> s;
for (int j = 0; j < v; j++) { // 按余数分组,组内向前依赖
// 查找指定范围内的最大值,标准的单调队列
int hh = 0, tt = -1;
for (int k = j; k <= m; k += v) { // 分组内枚举每个可能的体积
// 1、超出窗口范围的队头出队列,左侧只保留到k-s*v
if (hh <= tt && q[hh] < k - s * v) hh++;
// 2、处理队尾,下一个需要进入队列的是f[i-1][k],它是后来的,生命周期长,可以干死前面能力不如它的所有老头子,以保证一个单调递减的队列
while (hh <= tt && f[i - 1][q[tt]] + (k - q[tt]) / v * w <= f[i - 1][k]) tt--;
// 3、k入队列
q[++tt] = k;
// 4、上面操作完,f[i-1][k]已经进入队列,f[i][k]需要的所有人员到齐,可以直接从队头取出区间最大值更新自己了
f[i][k] = f[i - 1][q[hh]] + (k - q[hh]) / v * w;
}
}
}
printf("%d\n", f[n][m]);
return 0;
}
一维版本
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 20010;
int n, m;
int f[M], g[M];
int q[M];
int v, w, s;
// 一维写法
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
memcpy(g, f, sizeof g);
cin >> v >> w >> s;
for (int j = 0; j < v; j++) {
int hh = 0, tt = -1;
for (int k = j; k <= m; k += v) {
if (hh <= tt && q[hh] < k - s * v) hh++;
while (hh <= tt && g[k] >= g[q[tt]] + (k - q[tt]) / v * w) tt--;
q[++tt] = k;
f[k] = max(g[k], g[q[hh]] + (k - q[hh]) / v * w);
}
}
}
printf("%d\n", f[m]);
return 0;
}
七、疑问解答
\(Q1\):为什么可以引入单调队列对多重背包进行优化?
\(A\):因为朴素版本三层循环,太慢了,要想办法优化?怎么优化的呢?因为发现每个新值要想更新\(f[i][j]\)值,第\(i\)件物品,最多有\(s_i\)件,我们可以选择\(0 \sim s_i\)个,同时,由于\(i\)物品的体积是\(v_i\),也就是我们在拿物品\(i\)时,有一个关系
| 拿\(0\)个 | 拿\(1\)个 | 拿\(2\)个 | ... | 拿\(s\)个 | |
|---|---|---|---|---|---|
| 体积 | \(k\) | \(k-v\) | \(k-2*v\) | ... | \(k-s*v\) |
| 价值 | \(f[i-1][k]\) | \(f[i-1][k-v]+w\) | \(f[i-1][k-2*v]+2*w\) | ... | \(f[i-1][k-s*v]+s*w\) |
总结:
- 往前最多看\(s\)个
- \(f[i][j]\) 跳跃性依赖 于\(f[i-1][j - x * v]\),想要求什么呢?求离我距离最多\(s\)个数的最大值。这数不用每次现去查找,可用单调队列动态维护来优化查询。
\(Q2\):单调队列中装的是什么?
\(A\):是体积,是\(f[i][j]\)可以从哪些 体积 转移而来。比如当前\(i\)物品的体积是\(v_i=2\),个数是\(3\),那么\(f[i][j]\)可以从
转移而来,当然,还需要判断一下是不是你的背包能装下那么多,一旦装不下了就别硬装了。
\(Q3\):只记录体积怎么计算最大价值?
\(A\):只记录了所关联的体积,最大价值是现用现算的,办法是
即,自己的最优解,可以通过前序当中最大值所在的体积q[hh]转移而来,产生的增量价值就是 \(\large \displaystyle (k - q[hh]) / v * w\)
\(Q4\):单调队列的使用场景在哪里?
\(A\):使用单调队列的唯一场景就是 离我在\(X\)的范围内,最大或最小值是多少?
它的任务是做到\(O(1)\)的时间复杂度进行快速查询结果,所以,只能是放在队首,不能再进行遍历或者二分,那样就不是\(O(1)\)了。
\(Q5\):单调队列是怎么样做到将最优解放到队首的呢?
\(A:\)单调队列优化有三步曲,按套路做就可以完成这样的任务:
-
将已经超过 窗口范围 的旧数据从单调队列中去掉,保证窗口中只有最近的、最多\(s\)个(或\(s+1\),这和具体的题意有关,后续会继续说明~)有效数据。
-
利用队首中保存的体积,我们知道最大值的前序体积\(q[hh]\),从这个体积转移而来就行。
\[\large f[i][k] = f[i - 1][q[hh]] + (k - q[hh]) / v * w \] -
滑动窗口是建立在前序数组\(f[i-1]\)上的,范围只能是前面一行\(f[i-1][j],f[i-1][j-v],f[i-1][j-2v],...,f[i-1][j-kv]\)
\(Q6:\)此处的单调队列,是递增还是递减的?
\(A:\)是一个单调递减的队列,队列头存储的是窗口中的最大值所对应的体积。
\(Q7\):为什么要先进队列,再更新答案呢?我看有些同学是先更新答案,再进队列啊?
\(A\):这个主要看\(f[i-1][k]\)是不是可以成为答案的备选项,如果是,那么就先进队列,再更新;如果不是,则先更新再进队列。以本题为例,\(f[i][k]\)可不可以从\(f[i-1][k]\)迁移而来呢?从实际含义出发,是可以的,这表示:第\(i\)个物品一个也不要,在空间最大是\(k\)的情况下,最大值如何表示?此时,当然最大值表示为\(f[i-1][k]\)了,即可以成为答案的备选项,需要先进队列再更新答案。
\(Q8\):if (hh <= tt && q[hh] < k - s * v) hh++;
不是应该是\(0\)~\(s\)个物品\(i\)吗,不应该是\((k-q[hh])/v>s+1\)个项吗?
答:好问题!确实是\(0\)~\(s\)共\(s+1\)个,按理说单调队列长度最长应该是\(s+1\),这里为什么只有\(s\)个长度呢?
\(DP\)问题都可以视为一个填表求解的过程,比如本题就是一个二维表格的填充过程:
\(f[i][j]\):前\(i\)个物品中选择,在体积上限是\(j\)的情况下,所能获取到的最大价值。
从上到下,从左到右去填表,我们发现了以下的事实:
- 每一个二维表中的位置,都是可以从上一行中的某些位置转移而来的。比如:
\(f[i-1][j] -> f[i][j]\)
\(f[i-1][j-v]+w -> f[i][j]\)
\(f[i-1][j-2v]+2w -> f[i][j]\)
\(f[i-1][j-3v]+3w -> f[i][j]\)
....
\(f[i-1][j-s*v]+s*w -> f[i][j]\)
当然,这也不一定都对,因为要保证\(j-s*v>=0\)
这些数据依赖是 跳跃性的前序依赖,所以,我们按对体积取模的余数分组,按组讨论,就可以把二维表填充满。
-
它的前序依赖单元格个数是\(s\)(指最大值)个,我们需要在这些个值中找出一个\(max\)。这是一个 距离我最近\(X\)个元素内找出最大值的典型问题:单调递减队列求区间最大值,队头元素即答案。
-
\(Q\):为什么是单调队列呢?如何运用单调队列求解呢?
就是维护一个队列,它是由大到小的顺序单调存在的。对于后面每一个加入进来的数据,因为它是最新出生的,就算是最小,当前面老家伙们死光后,它也可能成为掌门人(黄鼠狼下豆鼠子,一辈不如一辈,这种情况就是可能的~),它必须保留!而它前面的老家伙,即使再厉害,由于年龄到了,也需要去世。没有来的及去世的老家伙们,因为能力值小于最后加入的数据,也就没有存在下去的必要,因为后面向前找,肯定先找到新出生而且能力值高的嘛,这些老家伙去世算了。
好了,我们成功的为最后加入的家伙找到了存在下去的必要性,没它可不行!!!
所以,我们视f[i - 1][k]为新出生的家伙,用它与之前的老家伙们\(PK\),而且,它还必须要参与到单调队列中去,它不能去世!
\(Q\):为啥要视它为最新出生的家伙,咋不视别人呢?
\(A\):往前倒着看,离自己最近,谁最近?因为这里的距离其实是按体积看的,和自己一样体积的单元格,在自己的正上方,上可以转移到\(f[i][j]\)的吧,\(f[i-1][k]\)当然是最后一个啦。
如果被它占了一个名额后,就剩下\(s\)个位置了。
同时,我们也注意到,就是因为上面讨论到的原因,使得在执行f[i][k] = f[i - 1][q[hh]] + (k - q[hh]) / v * w; 之前,需要执行 q[++tt]=k,让新出生的家伙进入队列,凑齐s+1个


