AcWing 1023. 买书
\(AcWing\) \(1023\). 买书
一、题目描述
小明有 \(m\) 块钱，现有 \(10\) 元， \(20\) 元， \(50\) 元， \(100\) 元 的书
每本书可以购买多次，求小明有多少种买书方案
输入格式
一个整数 \(n\)，代表总共钱数。
输出格式
一个整数，代表选择方案种数。
数据范围
\(0≤n≤1000\)
输入样例1：
20
输出样例1：
2
输入样例2：
15
输出样例2：
0
输入样例3：
0
输出样例3：
1
二、分析
一共有 \(n\) 个物品，每个物品有体积 \(v_i\)，价值 \(w_i\)，每个物品能够选多次
求总体积恰好是\(m\)的方案数
这是一道 裸的完全背包问题求解方案数
闫氏\(DP\)分析法
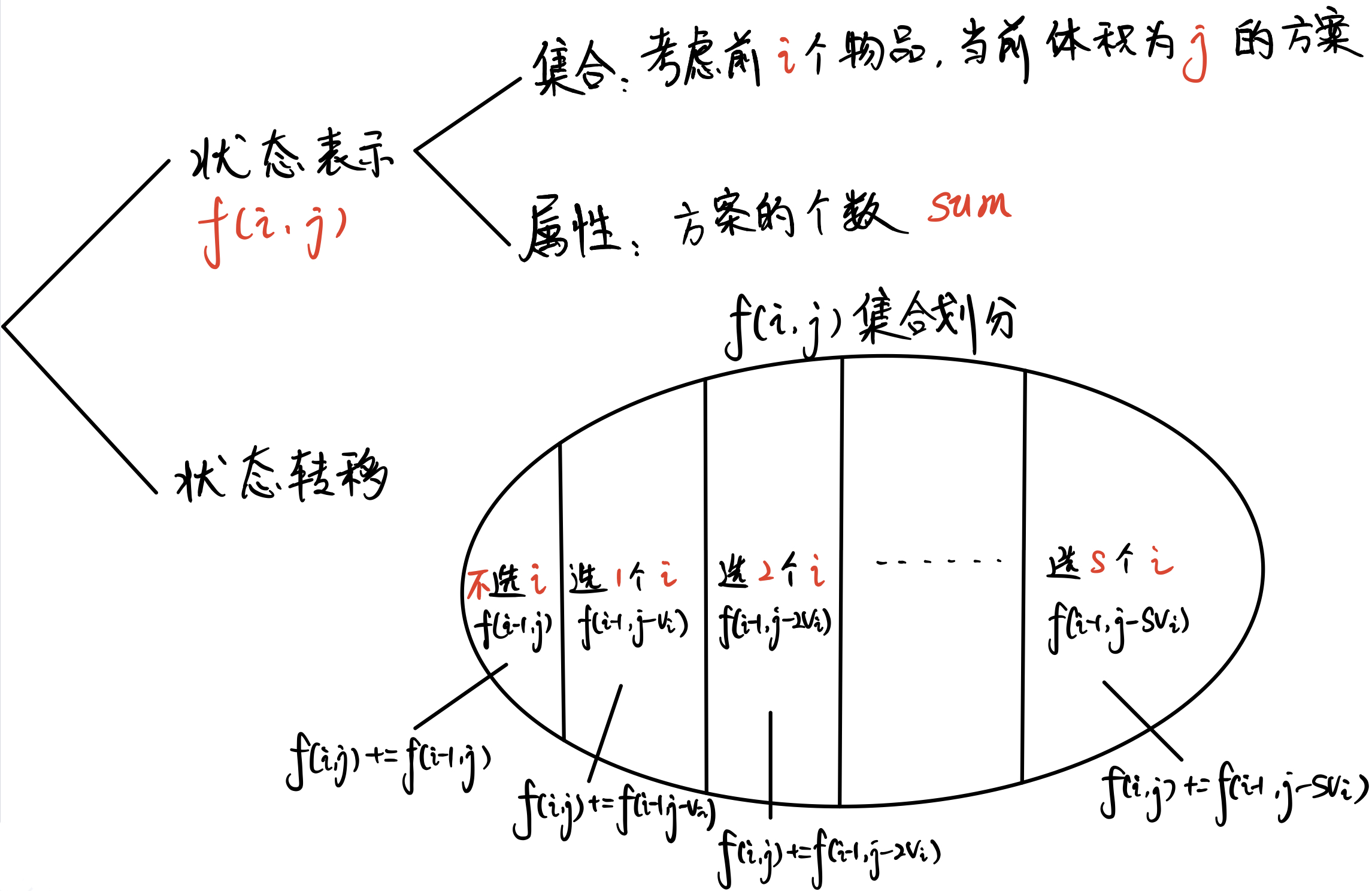
状态表示——集合：\(f[i][j]\) 表示考虑前\(i\)个数字，且总数字和恰好\(j\)的集合下能获得的方案数。
状态表示——属性：因为是求方案数，故为 \(count\)。
状态计算——集合划分：考虑第 \(i\) 个数选不选。
- 不选或选不了（剩余数量不够 \(j<a[i]\)）：\(f[i−1][j]\)。
- 选：\(f[i][j−a[i]]\)。
初始状态：\(f[0][0]\)
目标状态：\(f[n][m]\)
二、朴素版本
时间复杂度：\(O(n^2 \times m)\)
#include <bits/stdc++.h>
using namespace std;
const int N = 5;
const int M = 1010;
int v[N] = {0, 10, 20, 50, 100}; // 每种货币，下标从1开始
int n, m; // 货币种类，钱数
int f[N][M]; // 前i种物品，体积恰好是j的情况下的最大值
// 完全背包
int main() {
n = 4;
cin >> m;
// 前0种物品，体积是0的情况下只有一种方案
// 一般询问方案数的问题f[0]都会设置为1
// Q:那20元钱呢？不买；买两本10块的；每一本20的。三种呀
// A:题目说的全部，钱要花完
f[0][0] = 1;
for (int i = 1; i <= n; i++) // 每个物品
for (int j = 0; j <= m; j++) // 每个体积
for (int k = 0; v[i] * k <= j; k++) // 个数
f[i][j] += f[i - 1][j - v[i] * k];
printf("%d\n", f[n][m]);
return 0;
}
三、完全背包—经典优化
使用瞪眼大法，观察 \(f(i,j)\) 的 状态转移方程 进行变形
尝试找出\(f(i,j)\)与它的前序\(f(i,j-v_i)\)之间的关联关系，看看能不能实现\(f(i,j-v_i)->f(i,j)\)的迁移：
注：把体积\(j-v_i\)代入①式,就可以得到 ②式
\(Q:\)①和②中的\(s\)是一个值吗，为什么？
答：是一个值的。原因可以从事情本质出发，思考一下\(s\cdot v_i\)的含义是什么:就是在\(j\)这么大的空间限制下，最多可以装多少个\(i\)物品，当然是同一个个数值\(s\)了。
由上述两个等式可以获得如下递推式：
把这个等式作为 状态转移方程 ，就可以把时间复杂度优化到 \(O(n \times m)\)
同时，观察到该 转移方程 对于第 \(i\) 阶段的状态，只会使用第 \(i-1\) 层和第 \(i\) 层的状态
因此我们也可以采用 \(01\)背包 的 空间优化方案
时间复杂度：\(O(n×m)\)
空间复杂度：\(O(m)\)
二维优化版本
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int v[5] = {0, 10, 20, 50, 100};
int f[5][N];
int main() {
int m;
cin >> m;
// 前0种物品，体积是0的情况下只有一种方案
f[0][0] = 1;
for (int i = 1; i <= 4; i++)
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] += f[i][j - v[i]];
}
printf("%d\n", f[4][m]);
return 0;
}
一维优化解法
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int v[5] = {0, 10, 20, 50, 100};
int f[N];
// 体积限制是恰好是，因此需要初始化f[0][0]为合法解1，其他位置为非法解0。
int main() {
int m;
cin >> m;
// 前0种物品，体积是0的情况下只有一种方案
f[0] = 1;
for (int i = 1; i <= 4; i++)
for (int j = v[i]; j <= m; j++)
f[j] += f[j - v[i]];
// 输出
printf("%d\n", f[m]);
return 0;
}
