AcWing 275. 传纸条

\(AcWing\) \(275\). 传纸条

一、题目描述

给定一个 \(n×m\) 的矩阵，\(A\) 在矩阵左上角 \((1,1)\) 的位置，\(B\) 在矩阵右下角 \((n,m)\) 的位置

\(A\) 要向 \(B\) 传递一次纸条，且传递的过程只能向下或向右

\(B\) 也要向 \(A\) 传递一次纸条，且传递的过程只能向上或向左

两次过程中，经过的格子 不能重合

每个格子给定一个 好感度，其实就是这个格子的 价值

我们要找到一个 方案，使得两次传递的路线经过的所有格子的 价值最大

二、题目解析

这题明显不是一个裸题，我们需要一层一层的拆解分析

首先想到的是能不能往 方格取数 模型上靠

对于一个从 \((n,m)\) 出发到 \((1,1)\) 的路线，且只能向上或向左走，考虑将其方向调转，则必定对应一条从 \((1,1)\) 出发到 \((n,m)\) 的路线，且只能向下或向右走

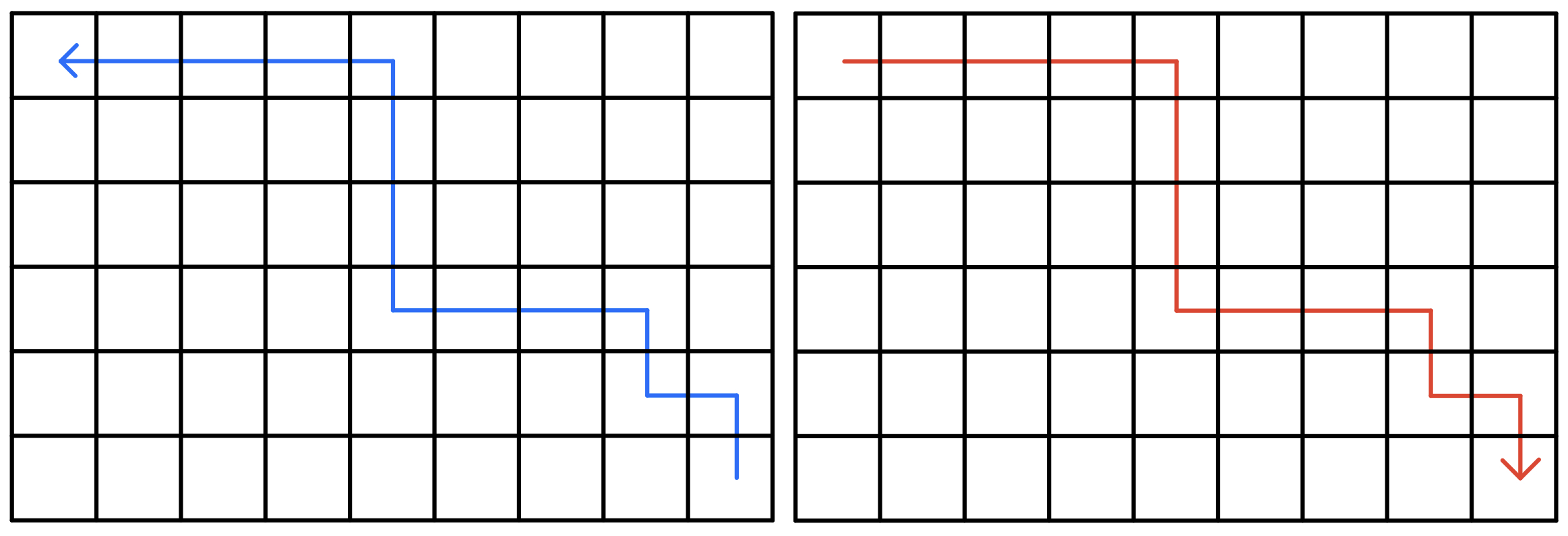
这两种走法的方案都是一一对应的（即任意一条路线都可以找到其对应的反向路线），因此该方案 映射合法

于是该问题就变成了寻找一条从 \((1,1)\) 出发到达 \((n,m)\)，每次只能向下或向右走，先后出发两次，且两次路线 不能经过重复格子 的 最大价值方案

这样就很靠近 方格取数 模型了

关于如何解决不能经过重复格子的问题

我们先给定一个结论： 方格取数 \(dp\)模型的最优方案可以是不经过重复格子的

证明：

情况一：最优解的两条路线是相互交叉经过的

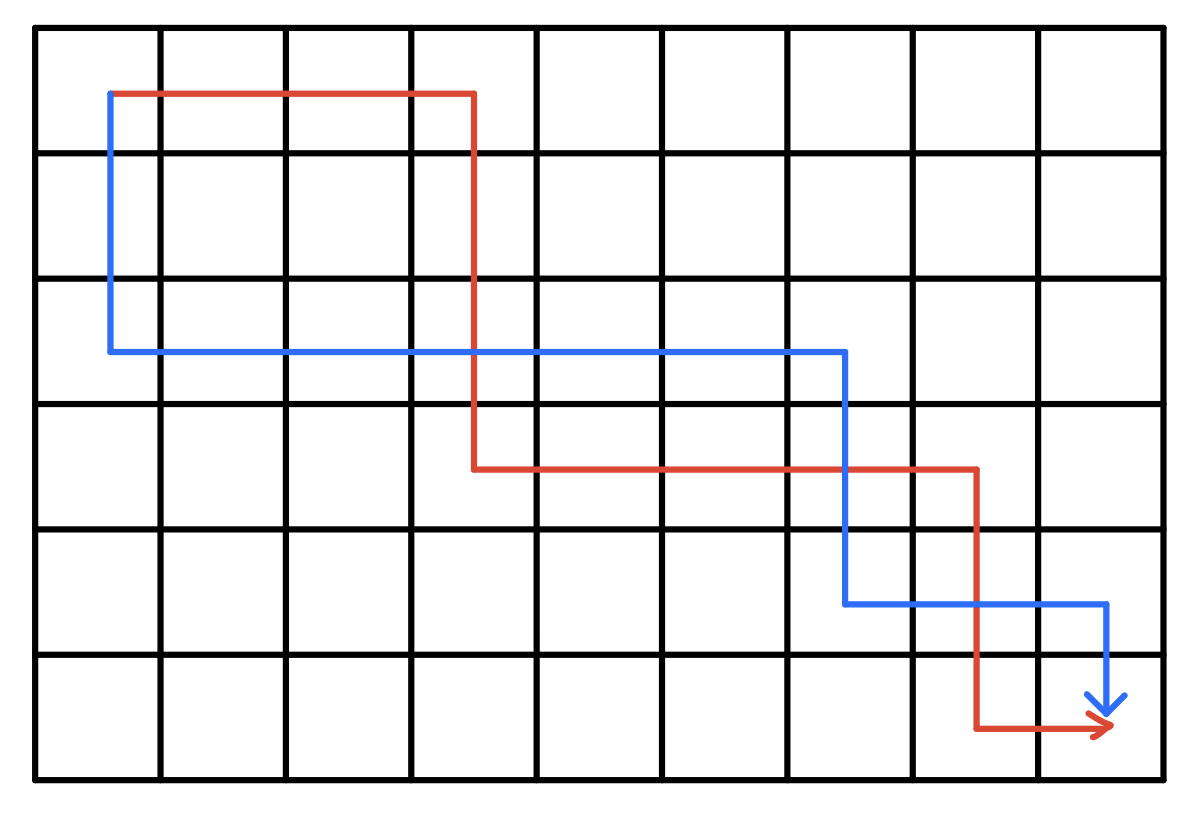
则我们可以对交叉出来的部分进行路线交换，如下图的操作

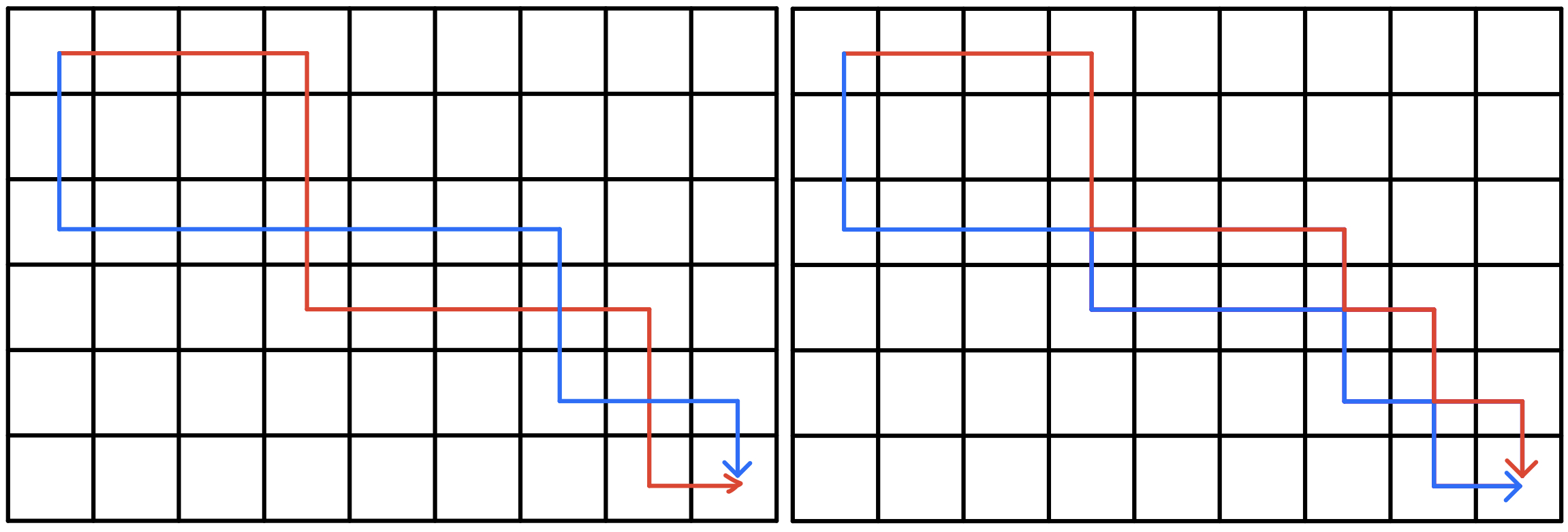
于是，我们可以发现，所有的交叉路线都会映射成一种一条路线 只在下方走，一条路线 只在上方走 的 不交叉路线

因此我们只需集中解决情况二即可

情况二：最优解的两条路线不交叉，但在某些点有重合

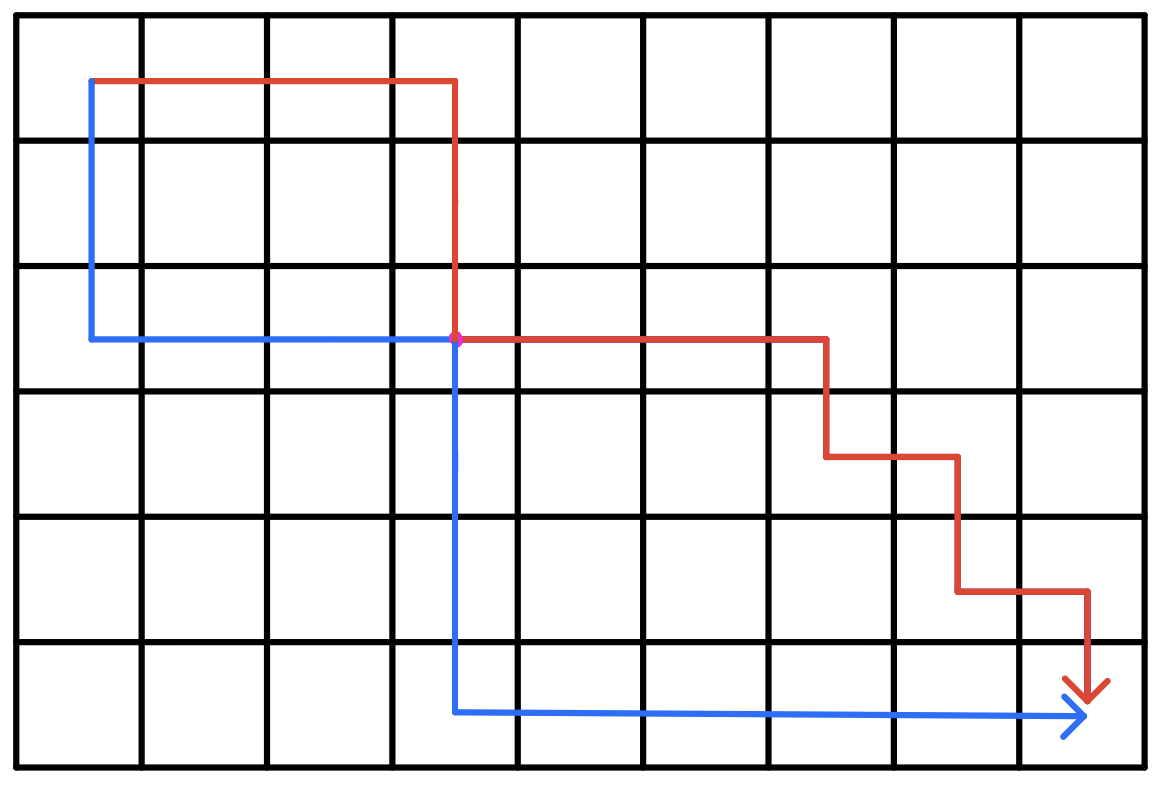
由于方格取数，对于走到相同格子时，只会累加一次格子的价值

于是我们可以使用 贪心 中的 微调法 来进行这部分的证明

对于 重合 的格子，我们必然可以在两条路线中找到额外的一条或两条路线，使得新的路线不发生重合

具体参照下图：

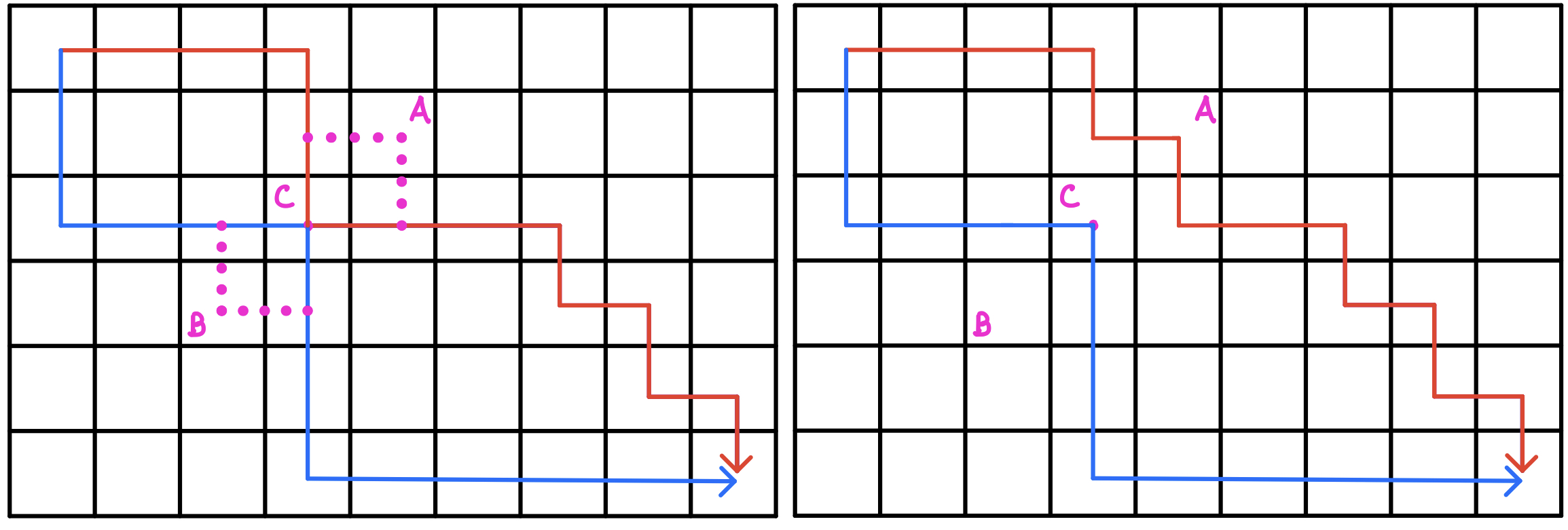
由于原路线是最优解，则必然 \(w_A=w_B=0\)，否则最优解路线必然是经过 \(A\) 或 \(B\) 的

因此，我们可以通过微调其中的一条路线，使之不经过重合点 \(C\)，同时路线的总价值没有减少

得证：最优解路线可以是不经过重复路线的 （部分证明方法参照了 第一赞的题解了）

接下来就是完全参照 \(AcWing\) \(1027\). 方格取数 的\(DP\)分析了

关于 重合格子 判断一些条件都在这篇博客里详细写了

这里我偷个懒，直接用我上篇博客的内容了 （既然是我自己写的应该不算抄袭吧！）

Code(三重迭代写法)

集合划分

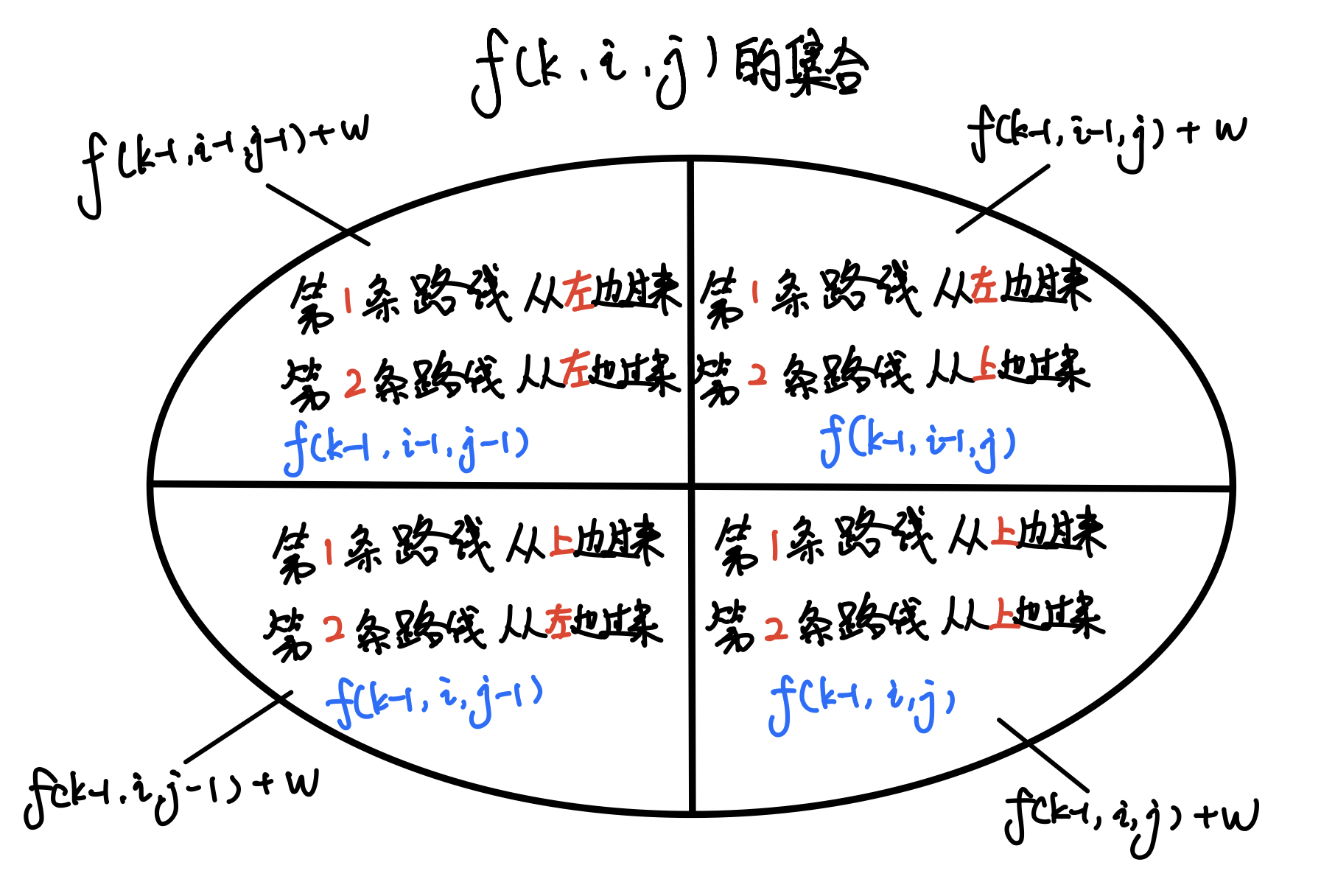
状态的初值: \(f[2][1][1]\)

目标的状态: \(f[n + m][n][m]\)

#include <bits/stdc++.h>

using namespace std;
const int N = 55;

int n, m;
int w[N][N];
int f[N * 2][N][N];

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> w[i][j];

    // 左上角是(1,1),k表示两个小朋友所在位置的x+y的和，最多是n+m
    for (int k = 2; k <= n + m; k++)
        for (int x1 = 1; x1 <= n; x1++)       // 第一个小朋友竖着走的距离
            for (int x2 = 1; x2 <= n; x2++) { // 第二个小朋友竖着走的距离
                int y1 = k - x1, y2 = k - x2; // 计算横着走的距离
                // 不能出界，只走有效的位置
                if (y1 < 1 || y1 > m || y2 < 1 || y2 > m) continue;

                // 将本位置的数值加上
                int &x = f[k][x1][x2];
                x = max(x, f[k - 1][x1 - 1][x2] + w[x1][y1]);
                x = max(x, f[k - 1][x1 - 1][x2 - 1] + w[x1][y1]);
                x = max(x, f[k - 1][x1][x2 - 1] + w[x1][y1]);
                x = max(x, f[k - 1][x1][x2] + w[x1][y1]);

                // 如果不是重复的位置，还可以继续加上
                if (x1 != x2) f[k][x1][x2] += w[x2][y2];
            }
    // 输出DP的结果
    printf("%d\n", f[n + m][n][n]);
    return 0;
}