AcWing 905. 区间选点
\(AcWing\) \(905\). 区间选点
一、题目描述
给定 \(N\) 个闭区间 \([a_i,b_i]\)，请你在数轴上 选择尽量少的点，使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
输入格式
第一行包含整数 \(N\)，表示区间数。
接下来 \(N\) 行，每行包含两个整数 \(a_i,b_i\)，表示一个区间的两个端点。
输出格式
输出一个整数，表示所需的点的最小数量。
数据范围
\(1≤N≤10^5\),
\(−10^9≤a_i≤b_i≤10^9\)
输入样例：
3
-1 1
2 4
3 5
输出样例：
2
二、题目解读
-
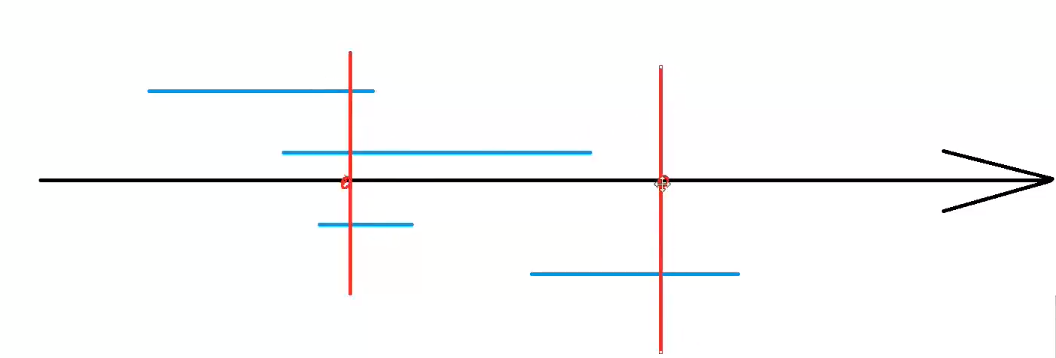
每个线段上最少要选择一个点
-
如果一个点同时出现在两个线段上，就可以节约掉一个点
给\(N\)个区间，问最少可以选择几个点,上图可以选择两个点。
三、解题思路
贪心问题，区间问题无外乎就是排序
- 按左端点排序
- 按右端点排序
- 双关键字排序（先按右端点，再按左端点）
如果没有思路就先试一下，举一些例子，感受一下是不是有问题，看看有什么规律没有。
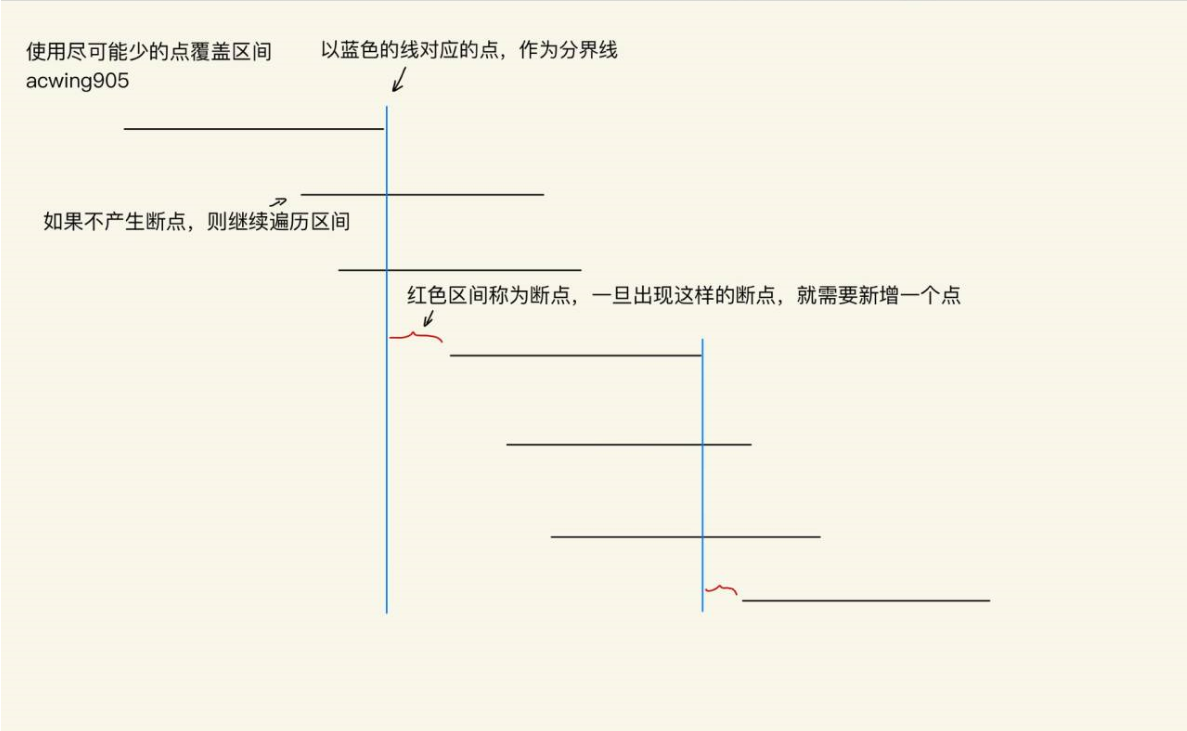
\(Q\):为啥要按右端点排序呢？
\(A\):选择右端点，就是想获取到本个线段的最大可以达到哪个位置，能获得最大的利益。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int n; // 线段数量
int res; // 结果
int ed = -INF; // 当前覆盖区间的结束边界，即右端点位置
// 结构体
struct Node {
int l, r;
// 按每个区间的右端点从小到大排序
const bool operator<(const Node &b) const {
return r < b.r;
}
} range[N];
int main() {
cin >> n;
// 注意这里的数组下标是从0开始的
for (int i = 0; i < n; i++) cin >> range[i].l >> range[i].r;
// 右端点从小到大排序，排序也需要从数组下标1开始
sort(range, range + n);
// 思想：① 所有区间按右端点从小到大排序
//② 遍历每一个区间，如果当前区间的左与前一个区间的右有交集，则只需要一个点就可以覆盖掉两个区间
for (int i = 0; i < n; i++)
if (range[i].l > ed) {
res++;
ed = range[i].r;
}
cout << res << endl;
return 0;
}
四、\(PII\)简化版本
#include <bits/stdc++.h>
using namespace std;
#define l second
#define r first
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
int n;
PII a[N];
/*
由于pair会自动以first升序排列所以用pair就不用自己重载小于运算符，至于first和second的先后关系其实没什么意义。
只要在输入/存储时交换一下x,y顺序即可，如果觉得容易混可以直接定义l为second,r为first就不会混了，同理以左端点排序的题一样
*/
int res, ed = -INF;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
a[i] = {y, x};
}
sort(a, a + n);
for (int i = 0; i < n; i++) {
if (a[i].l > ed) {
res++;
ed = a[i].r;
}
}
cout << res << endl;
return 0;
}
五、贪心思路证明
要想看懂\(Y\)总的证明，关键是要弄清楚\(cnt\)的含义究竟是什么，其实\(cnt\)有两个含义:
①是指，按照各区间按右端点从小到大排，再从前往后枚举各区间，若当前区间中已包含之前被选的区间右端点，则直接跳过该区间；否则，选择当前区间的右端点这样的贪心思路所选出来的右端点的数量。
②是指，所有区间中一定存在\(cnt\)个两两之间没有交集的区间。因为各区间按照右端点排序后，每一个被选择的区间右端点（共\(cnt\)个）都是没有被 （被选择的排序位置更靠前的区间的右端点） 覆盖到的区间的 右端点。
证明
①假设最优解为\(ans\)个，以上述贪心思路选出来的点为\(cnt\)个。即证明\(ans == cnt\)，等价于证\(ans >= cnt\) 同时 \(ans <= cnt\)
②首先，以上述贪心思路选择出的\(cnt\)个点，是一组可行方案。其覆盖了所有区间，满足题目要求。又因为\(ans\)是最优解，即为所有可行方案的最小值，那么最优解\(ans <= cnt\)成立
③其次由于所有区间中一定存在\(cnt\)个两两之间没有交集的区间，那么至少需要\(cnt\)个点才能将这些两两不交的区间进行覆盖，又因为题目要求选的点还要能覆盖所有别的区间，故最优解\(ans >= cnt\)成立
