AcWing 291. 蒙德里安的梦想
\(AcWing\) \(291\). 蒙德里安的梦想
一、题目描述
求把 \(N×M\) 的棋盘分割成若干个 \(1×2\) 的长方形，有多少种方案。
例如当 \(N=2，M=4\) 时，共有 \(5\) 种方案。当 \(N=2，M=3\) 时，共有 \(3\) 种方案。
如下图所示：
输入格式
输入包含多组测试用例。
每组测试用例占一行，包含两个整数 \(N\) 和 \(M\)。
当输入用例 \(N=0，M=0\) 时，表示输入终止，且该用例无需处理。
输出格式
每个测试用例输出一个结果，每个结果占一行。
数据范围
\(1≤N,M≤11\)
输入样例：
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例：
1
0
1
2
3
5
144
51205
二、核心思想
1、先放横的，再放竖的
理由：如果把横的全部放完，其它的空位用竖的放就行啦,此时，竖的放法只有一种。
2、总方案数等于只放横的 合法方案数
\(Q\):如何判断方案是否合法？
当前摆完横着的小方块之后，剩余的位置，如果能用竖着的小方块 填满 就合法，否则不合法。
具体的办法按列看：
- 如果每一列所有连续空着的小方块个数是偶数个,可以用竖的填满
- 如果每一列所有连续空着的小方块个数存在奇数个,必然填充不满
三、动态规划
1、状态表示
\(\large f[i][j]\):已经摆完前\(i\)列并且第\(i\)列的状态为\(j\)的所有方案。
对于\(j\)这个二进制数中的\(1\)是指我在这个小方格 新 放置了一个横条。也就是这个小方格是一个横条的起始位置。
\(j\)是一个二进制数，用来表示哪一行的小方块是横着放的，其位数和棋盘的行数一致。
具体的实现：用一个\(N\)位(\(N\)是指行数)的二进制数，每一位\(0/1\)表示不同的状态,\(0 → 2^N − 1\) （ \(N\) 二 进 制 对 应 的 十 进 制 数 ）中的所有数来枚举全部的状态。
解释：上图中 \(i=2\)，\(j =10101\)（二进制数，但是存的时候用十进制 ） 所以这里的\(f[i][j]\) 表示的是所有前\(i-1\)列摆完之后，从第 \(i-1\)列伸到第\(i\)列的状态是\(10101\)（第\(1\)行伸出来，第\(3\)行伸出来，第\(5\)行伸出来，其他行没伸出来）的方案数。
2、初始化
初始化\(f[0][0]=1\)也好理解一些。因为我们正常摆第一列的时候是随便自由摆放的，所以\(f[0][i]\)中除了\(f[0][0]\)其他的都应该是非法的，赋值为\(0\)（因为如果\(i\)不是\(0\)，就代表有些小方格会放置横条，就会影响到第一列的摆放），而对于\(f[0][0]\)其含义是已经摆完了前\(0\)列并且第\(0\)列的状态是\(0\)，也就是这一列没有任何一个小方格放置了横条。其摆法只有一种所以赋值为\(1\)。
3、答案在哪
对于\(f[m][0]\)也就是已经摆完第\(m\)列，并且第\(m\)列的状态为\(0\)，也就是第\(m\)列没有任何一个小方格新去摆放横条，这正好就是我们想要的结果。
4、状态转移
第\(i-1\)列的某种状态，与第\(i\)列的某种状态之间，可能能转移，也可能无法转移。
思考：什么情况下会不存在转换关系?
(1)、寻找兼容状态
如果\(i-2\)想在当前行 伸出 一个小方格，而\(i-1\)列也想向下一列 伸出 一个小方格，就是冲突。
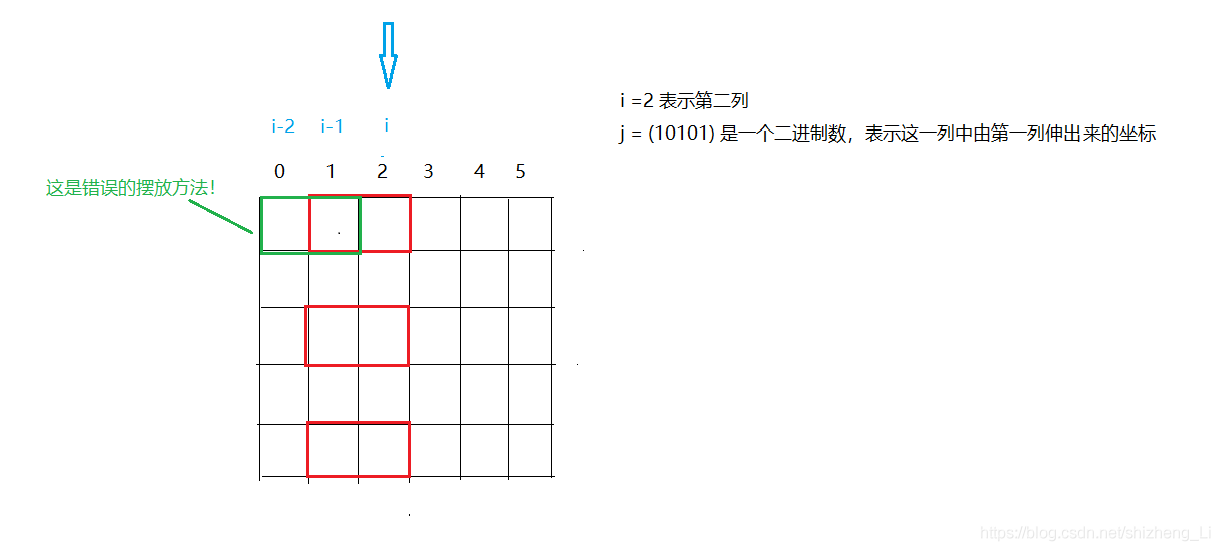
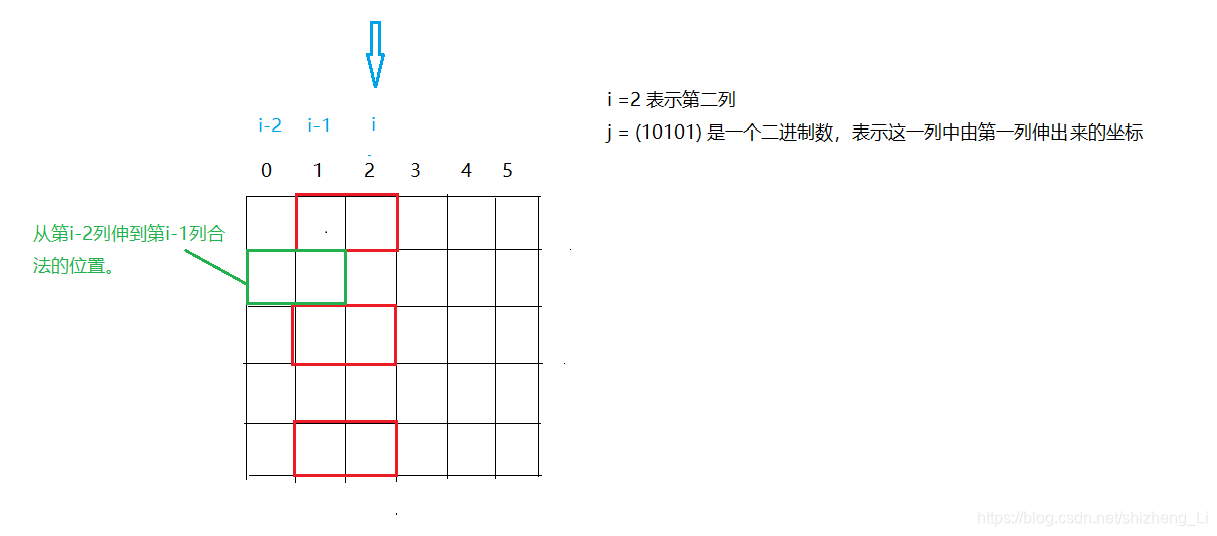
代码解读：对应的代码为
(i & j ) ==0，表示 \(i\)和\(j\)没有\(1\)位相同，即没有\(1\)行有冲突。此处的位运算大大提高了两种状态冲突检测的效率！，如果不用位运算，循环应该是跑不了的！
结论：通过分析判断出冲突状态，也就是找出了所有状态间的兼容关系，每个状态，只能从与自己兼容的状态转移过来，这是可以提前预处理出来的。
(2)、无效状态检查
是不是状态不冲突就可以转化了呢？不是的，举个栗子吧：两种状态不冲突:
\(i-2\)列有一个状态：\(00100\),\(i-1\)列有一个状态：\(01010\),它们两个之间是没有重叠的，不违反上面的第一条规则，但依然是有问题的：
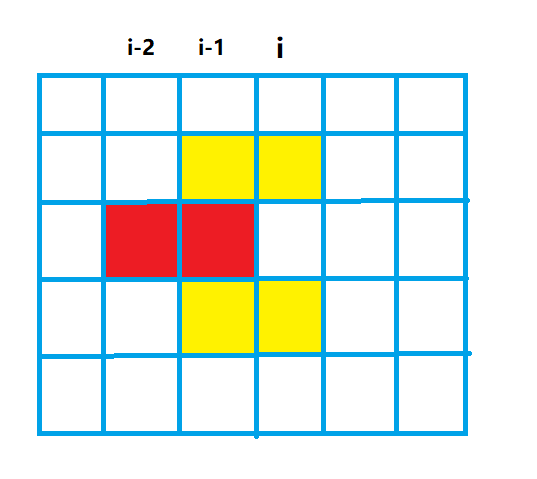
它会造成\(i-1\) 列无法继续用竖着的小方格填充满！！！
既然从第\(i-1\)列到第\(i\)列横着摆的，和第\(i-2\)列到第\(i-1\)列横着摆的都确定了，那么第\(i-1\)列 空着的格子就确定了，这些空着的格子将来用作竖着放。如果某一列有这些空着的位置，那么该列所有连续的空着的位置长度 必须是偶数 。
结论：啥样的状态是有效的，啥样的状态是无效的，是可以提前处理出来的。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 12;
const int M = 1 << N;
int n, m;
LL f[N][M]; // 已经摆完前i列并且第i列的状态为j的所有方案
vector<int> v[M]; // 对于每个状态而言，能转转移到它的状态有哪些，预处理一下(二维数组)
int ok[M]; // 某种状态是否合法，就是是不是存在奇数个连续0
int main() {
while (cin >> n >> m, n + m) {
// ① 预处理：枚举行数n的每个二进制位,可以枚举出每种可能出现的状态对应的二进制表示，这些状态有些是不合法的
// 只有不存在连续奇数个数字0的状态才是合法的，一旦n确定了，这个有效状态是可以预处理出来的
for (int i = 0; i < 1 << n; i++) {
int cnt = 0; // 连续0的个数
ok[i] = 1; // 初始设置此状态是合法的
for (int j = 0; j < n; j++) // 遍历此状态的每一个二进制位,开始检查
if (i >> j & 1) { // 如果本位是1,表示连续0发生中断，需要统计连续0的个数，并且记得清空cnt
if (cnt & 1) { // 奇数个连续0, (cnt & 1) = (cnt % 2 >0)
ok[i] = 0; // 连续0发生中断,此状态为不合法状态
break; // 不用再往后看了，一次失足就不挽救
}
cnt = 0; // 连续个零计数重新开始
} else
cnt++; // 连续0的计数器++
// 最后一个cnt++后，依然可能有连续奇数个，举个栗子：n=4=(0100)_2，完成数位枚举后，cnt=1,也就是高位存在奇数个0
if (cnt & 1) ok[i] = 0;
}
// ② 预处理：枚举每个状态，获取可能是从哪些有效状态转移过来
for (int i = 0; i < 1 << n; i++) {
// 多组数据，每次预处理时清空一下
// vector<int> v[M] 是一个二维数组，初始化比较麻烦，需要用循环遍历第一维，然后再v[i].clear()进行清空
v[i].clear();
// 状态i,从哪些状态转化而来？
for (int j = 0; j < 1 << n; j++) // j为前序状态
// (1) i & j==0 同一行不能同时探出小方格，那样会有重叠
// (2) 解释一下ok[i | j]
// 比如: 01000 | 10101 = 11101,描述当前完成状态叠加后的最终状态，在预处理的数组中找一下，是不是合法状态
if ((i & j) == 0 && ok[i | j]) v[i].push_back(j);
}
// 多组数据，每次清零
memset(f, 0, sizeof f);
// 初始方案数
f[0][0] = 1; // 可以理解为 从虚拟的第0开始（第一个0），还没有向右探出小方格（第二个0），此时的方案数只有1种。
// 如果你想为什么不是0种，下面的递推关系就会让你明白，0做为基底，就啥也递推不出来了。
// DP正式开始
for (int i = 1; i <= m; i++)
for (int j = 0; j < 1 << n; j++) // 遍历第i列的所有状态j
for (auto k : v[j]) // 遍历第i-1列的所有状态k
f[i][j] += f[i - 1][k]; // 每个合法状态，均需从它的前序有效状态转移而来
// 输出答案
cout << f[m][0] << endl;
}
return 0;
}
