AcWing 893. 集合-Nim游戏

$AcWing$ $893$. 集合-$Nim$游戏

一、题目描述

给定 $n$ 堆石子以及一个由 $k$ 个不同正整数构成的数字集合 $S$。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 $S$，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 $k$，表示数字集合 $S$ 中数字的个数。

第二行包含 $k$ 个整数，其中第 $i$ 个整数表示数字集合 $S$ 中的第 $i$ 个数 $s_i$。

第三行包含整数 $n$。

第四行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 堆石子的数量 $h_i$。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
$1≤n,k≤100,1≤s_i,h_i≤10000$

输入样例：

2
2 5
3
2 4 7

输出样例：

Yes

二、理论知识

理解题意：
集合$S$中有两个数($k=2$),分别是$2$和$5$。也就是拿一次不是任意个，是必须$2$或$5$个。
有$3$堆石子，个数分别是$2,4,7$。问我们是先手必胜还是先手必败。

• $mex$函数

  对于集合$S$,$mex(S)=mex(\{x_1,x_2…\})$表示$S$中没有出现的最小非负整数。

  例如:$S=\{0,1,2,4\}$,那么$mex(S)=3$。

• $sg$函数
  $sg(n)=mex(\{sg(i_1),sg(i_2),sg(i_3)...\})$。 $n$为结点；$i_1,i_2,i_3$…是$n$的后继结点。

• 规定
  $sg(G)=sg(head)$。 $G$是一个有向图,$head$是$G$的头结点。

• 结论
  $sg(G1)$ ^ $sg(G2)$ ^ $sg(G3)$ ^ $…$ ^ $sg(Gn)$为$n$个有向图的异或和,对于$n$个有向图游戏,这个异或和就是它的答案。

三、实例解析

$SG$函数是解决博弈论问题的一把利器。

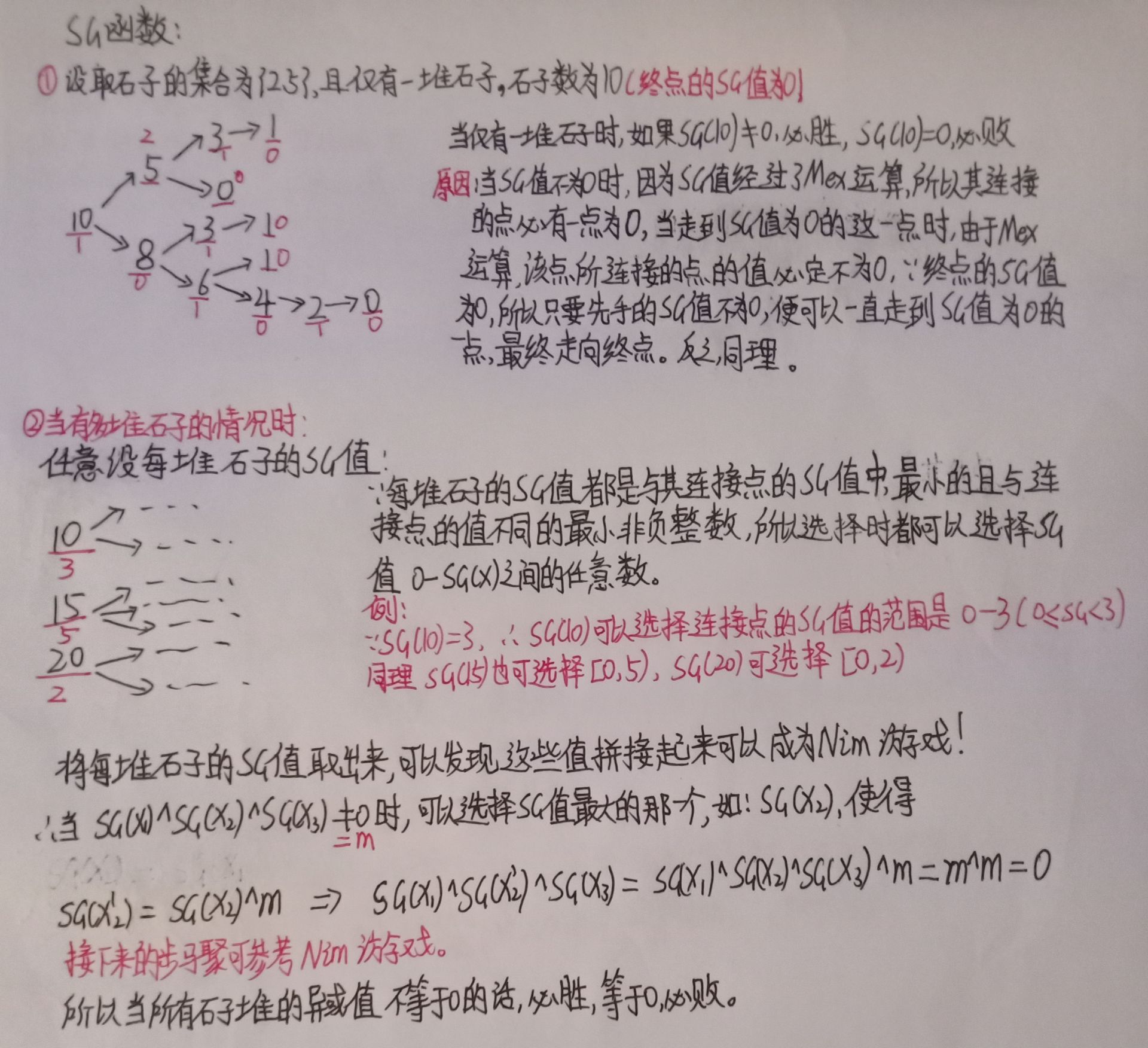
四、$SG$函数复用的原因

五、实现代码

#include <bits/stdc++.h>

using namespace std;

const int N = 110;
const int M = 10010;

int n, k;
int a[N]; // 一共几种取法，比如一次取2个或5个。
int f[M]; // SG函数的值
int res;

int sg(int x) {
    if (~f[x]) return f[x]; // 记忆化搜索

    unordered_set<int> S;
    for (int i = 0; i < k; i++)
        if (x >= a[i]) S.insert(sg(x - a[i])); // x-s[i]:x的可行路径中终点有哪几个; sg(x-s[i]):这个终点它的sg值

    for (int i = 0;; i++)
        if (!S.count(i)) return f[x] = i;
}

int main() {
    memset(f, -1, sizeof f); // 初始化数组值为-1
    cin >> k;                // 表示数字集合S中数字的个数
    for (int i = 0; i < k; i++) cin >> a[i];

    cin >> n; // 一共几堆
    // n堆石子，每堆石子都取SG值，然后异或在一起
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x; // 每堆里多少个
        res ^= sg(x);
    }
    if (res)
        puts("Yes"); // 如果不是零，必胜
    else
        puts("No"); // 如果是零，必败

    return 0;
}