AcWing 889. 满足条件的01序列

\(AcWing\) \(889\). 满足条件的01序列

一、题目描述

给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，它们将按照某种顺序排成长度为 \(2n\) 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 \(0\) 的个数都不少于 \(1\) 的个数的序列有多少个。

输出的答案对 \(10^9+7\) 取模。

输入格式
共一行，包含整数 \(n\)。

输出格式
共一行，包含一个整数，表示答案。

数据范围
\(1≤n≤10^5\)

输入样例：

3

输出样例：

5

二、卡特兰数

卡特兰数（\(Catalan\) \(number\)）是 组合数学 中一个常出现在各种 计数问题 中的 数列。

数列的前几项为：\(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862，...\)

下面将会选取几个 经典的卡特兰问题，难度先易后难，带领同学们逐个击破解决，最后给出相关的解题模板。

1、进出栈序列

这是一道 最经典 的入门级卡特兰数题目，如果能把这题看懂，相信后面的题目也能迎刃而解。

题目描述
\(n\) 个元素 进栈序列 为：\(1，2，3，4，...，n\)，则有多少种 出栈序列。

思路
我们将进栈表示为 \(+1\)，出栈表示为 \(-1\)，则 \(1->3->2\) 的出栈序列可以表示为：\(+1 -1, +1, +1, -1, -1\)。

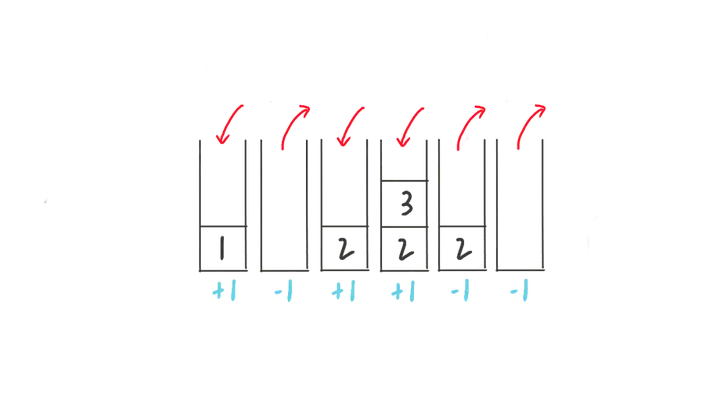
根据栈本身的特点，每次出栈的时候，必定之前有元素入栈，即对于每个\(-1\)前面都有一个\(+1\) 相对应。因此，出栈序列的 所有前缀和 必然大于等于 \(0\)，并且 \(+1\) 的数量 等于\(-1\) 的数量。

接下来让我们观察一下 \(n = 3\) 的一种出栈序列：\(+1, -1, -1, +1, -1, +1\)。序列前三项和小于 \(0\)，显然这是个 非法的序列 。

如果将 第一个 前缀和小于 \(0\) 的前缀，即前三项元素都进行取反，就会得到：\(-1, +1, +1, +1, -1, +1\)。此时有 \(3 + 1\) 个 \(+1\) 以及 \(3 - 1\) 个 \(-1\)。

因为这个小于 \(0\) 的前缀和必然是 \(-1\)，且 \(-1\) 比 \(+1\) 多一个，取反后，\(-1\) 比 \(+1\) 少一个，则 \(+1\) 变为 \(n + 1\) 个，且 \(-1\) 变为 \(n - 1\) 个。进一步推广，对于 \(n\)个元素的每种非法出栈序列，都会对应一个含有 \(n + 1\) 个 \(+1\) 以及 \(n - 1\)个 \(-1\) 的序列。

解读：

• 非法序列\(A\) 满足\(+1\)和\(-1\)的数量一样,这样不好处理，需要转化
• 转化思路是将第一个 前缀和 为\(-1\)的前\(m\)项取反,得到新序列\(B\)
• \(A\)和\(B\)是一一对应的，求出\(B\)序列数量，也就是求出了\(A\)序列数量
• 新序列\(B\)中存在一个规律，就是包含\(n\)个元素的序列，长度应该是\(2n\),存在\(n+1\)个\(+1\),\(n-1\)个\(-1\)

\(Q\):如何证明这两种序列是一一对应的？
假设非法序列为 \(A\)，对应的序列为 \(B\)。每个 \(A\) 只有一个 第一个前缀和小于\(0\)的前缀，所以每个 \(A\) 只能产生一个 \(B\)。而每个 \(B\) 想要还原到 \(A\)，就需要找到 第一个前缀和大于 \(0\) 的前缀，显然 \(B\) 也只能产生一个 \(A\)。

每个 \(B\) 都有 \(n + 1\) 个 \(+1\) 以及 \(n - 1\) 个 \(-1\)，因此 \(B\) 的数量为 \(C_{2n}^{n+1}\) ，相当于在长度为 \(2n\) 的序列中找到\(n + 1\)个位置存放 \(+1\)。相应的，非法序列的数量也就等于 \(C_{2n}^{n+1}\)。

出栈序列的总数量共有 \(C_{2n}^n\) ，因此，合法的出栈序列的数量为\(\large C_{2n}^n-C_{2n}^{n+1}=\frac{C_{2n}^n}{n+1}\) 。

此时我们就得到了卡特兰数的通项 \(\large \frac{C_{2n}^n}{n+1}\) ，至于具体如何计算结果将会在后面进行介绍。

2、括号序列

题目描述
\(n\) 对括号，则有多少种 括号匹配 的括号序列

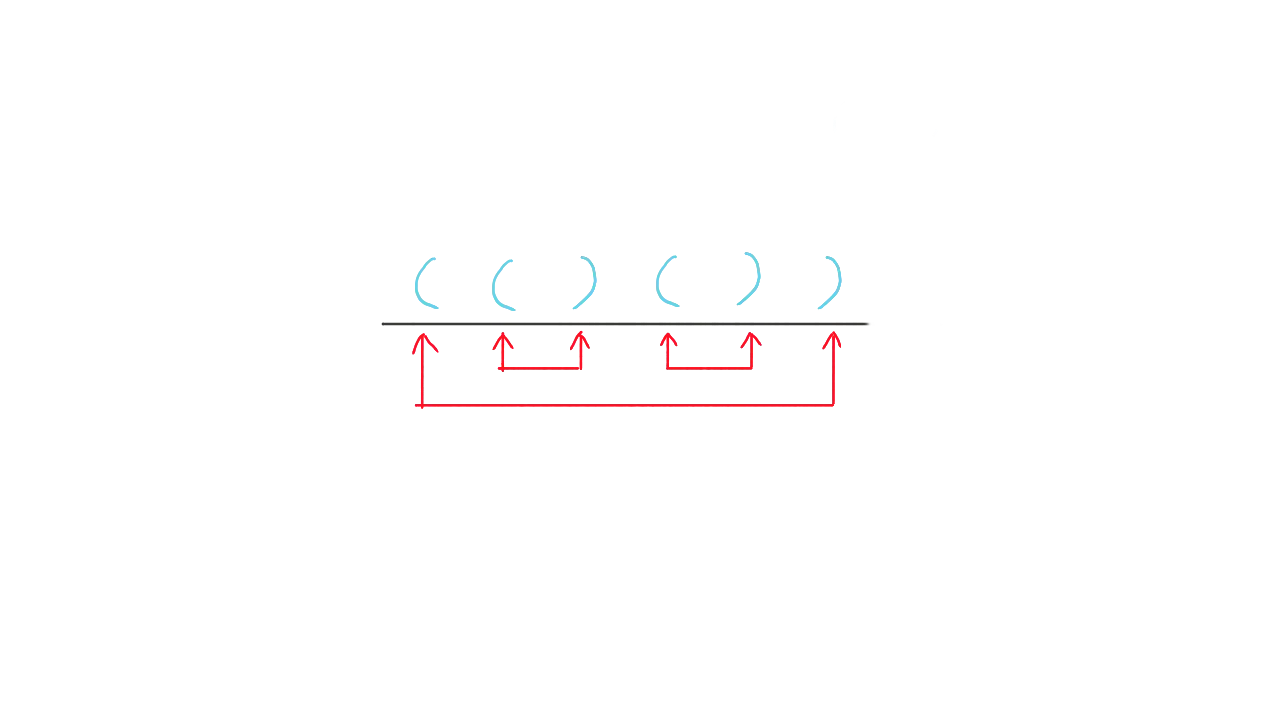
思路

左括号看成 \(+1\)，右括号看成 \(-1\)，那么就和上题的进出栈一样，共有 \(\large \frac{C_{2n}^n}{n+1}\) 种序列。

3、二叉树

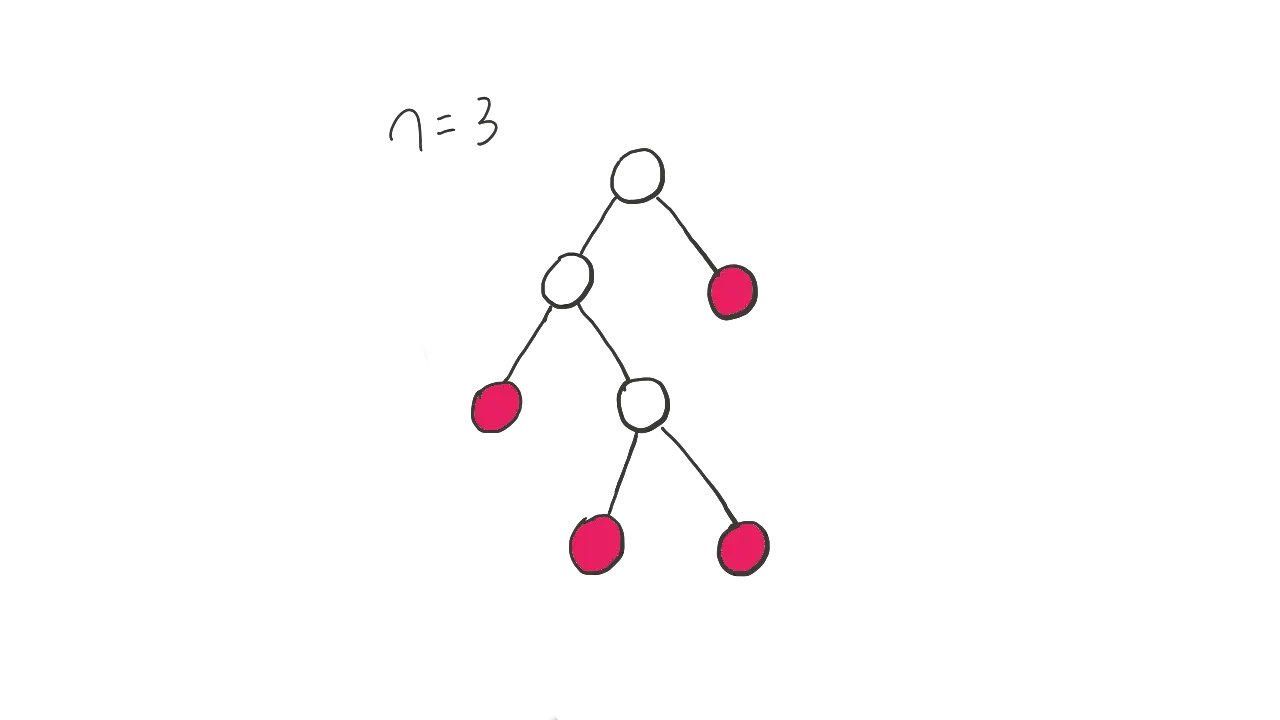
题目描述

\(n + 1\) 个叶子节点能够构成多少种形状不同的（国际）满二叉树

（国际）满二叉树定义：如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。

思路

使用深度优先搜索这个 满二叉树，向左扩展时标记为 \(+1\)，向右扩展时标记为 \(-1\)。

由于每个非叶子节点都有两个左右子节点，所有它必然会 先向左扩展，再向右扩展。总体下来，左右扩展将会形成匹配，即变成进出栈的题型。\(n + 1\)个叶子结点会有 \(2n\) 次扩展，构成 \(\large \frac{C_{2n}^n}{n+1}\) 种形状不同的满二叉树。

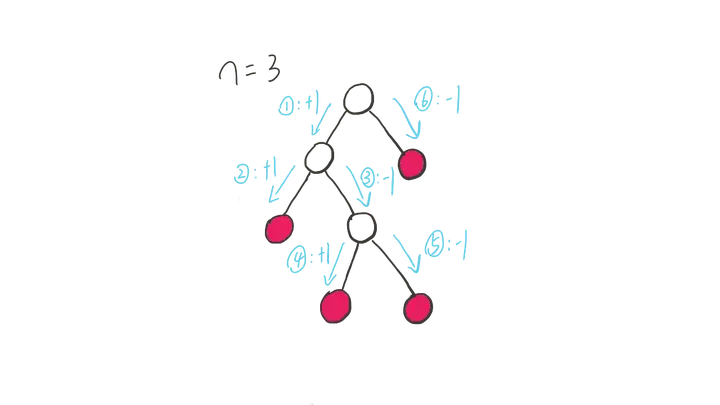
解读：

• 国际满二叉树与国内教材的满二叉树不一样，详细区别看 这里
• 国际满二叉树中，如果有\(n+1\)个叶子节点，则有\(n\)个非叶子节点，每个非叶子节点引出两条边，共\(2n\)条边
• \(2n\)条边，应该是先左，后右，即\(+1\)与\(-1\)和栈的那个一样，归到第一题的思路上去

4、电影购票

电影票一张 \(50\) \(coin\)，且售票厅没有 \(coin\)。\(m\) 个人各自持有 \(50\) \(coin\)，\(n\) 个人各自持有 \(100\) \(coin\)。

则有多少种排队方式，可以让每个人都买到电影票。

思路

持有 \(50\) \(coin\) 的人每次购票时不需要找零，并且可以帮助后面持有 \(100\) \(coin\) 的人找零；而对于持有 \(100\) \(coin\) 的人每次购票时需要找零，但 \(100\) \(coin\) 对后面的找零没有任何作用。

因此，相当于每个持有 \(100\) \(coin\) 的人都需要和一个持有 \(50\) \(coin\) 的人进行匹配。我们将持有 \(50\) \(coin\) 的标记为 \(+1\)，持有 \(100\) \(coin\) 的标记为 \(-1\)，此时又回到了进出栈问题。

不同的是，\(m\) 并一定等于 \(n\)，且排队序列是一种排列，需要考虑先后顺序，例如各自持有 \(50\) \(coin\) 的甲和乙的前后关系会造成两种不同的排队序列。所以，将会有 \((C_{m+n}^m-C_{m+n}^{m+1})*m!*n!\)

第二项为什么是 \(C_{m+n}^{m+1}\) ，其实很简单，我们每次把第一个前缀小于\(0\) 的前缀取反后，会造成 \(+1\) 多了一个而 \(-1\) 少了一个。这里 \(+1\) 有 \(m\) 个，\(-1\) 有 \(n\) 个，取反后 \(+1\) 变成\(m + 1\)个，\(-1\) 变成\(n - 1\)个，总和不变。

三、图形化推导

华罗庚:数缺形时少直观,形少数时难入微

下图表示所有在\(n×n\)格点中 不越过对角线的单调路径的个数（只向上向右走）

\(\large \frac{C_{2n}^n}{n+1}=C_{8}^{4} ÷ 5=(8*7*6*5)÷(5*4*3*2*1)=14\)

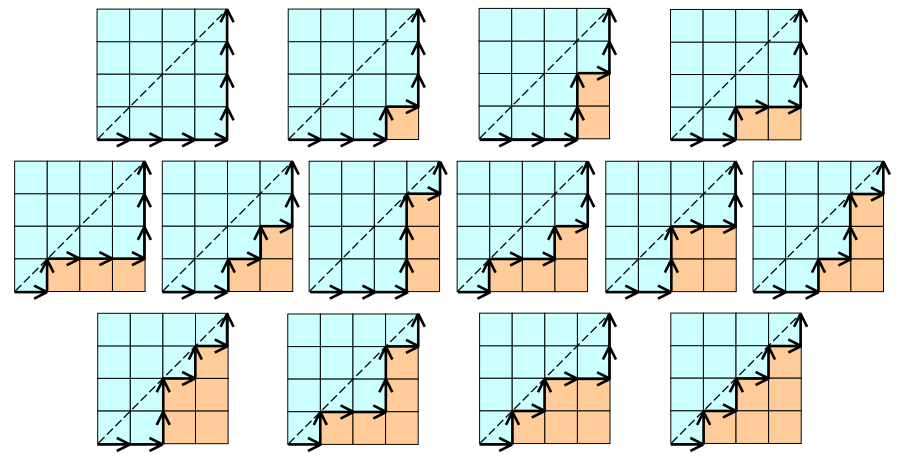
• 不考虑不越过对角线这个条件，有\(C_{2n}^{n}\)种方案

  解释：联想一下上面的\(-1,+1\)的序列摆上，共\(2n\)个，然后找出\(n\)个位置使用\(+1\)

• 对每个越过对角线的不合法方案，一定经过\(y=x+1\)这条直线，从路径与该直线的第一个交点处开始，剩余路径进行镜像处理（关于直线对称），终点一定是\((n,n)\)关于直线的对称点\((n−1,n+1)\)
  每一条\((0,0)−>(n−1,n+1)\)的路径，对应一条计数的非法路径，所以合法路径数为\(C_{2n}^{n}-C_{2n}^{n-1}\)

没看懂？理解一下:

假设\(n=6\):

1、方案总数

从\((0,0)\)到\((6,6)\)共有多少种合法走法?

因为从\((0，0)\)到\((6,6)\) 共需要向上共走\(6\)步，向右共走\(6\)步，一共\(12\)步。

每步两种选择，向上或向右，共\(2\)种选择。

如果在其中某\(6\)个步骤中选择向上走，那么剩下的\(6\)个步骤就是向右走。

向上走的方案数就是\(\large C_{12}^6\),向上的方案数定了，其它的步骤只能是向右的，最终的方案数是\(\large C_{12}^6\) 。

2、灰线数量计算

每一条黑线，一旦越过红线的部分，都可以根据红线做轴对称，画出对称的灰线。这样，所有到\((6，6)\)的黑线，都可以找到一条到\((5,7)\)的灰线，换句话说，只要计算出从\((0,0)\)到\((5,7)\)的方案数，也就是到\((0,0)\)到\((6,6)\)的越红线（也就是黑线）的方案数个数,从\((0,0)\)到\((5,7)\)的方案数：\(\large C_{12}^5\)。

3、合法方案数

\(C_{12}^{6} - C_{12}^{5}\)

这是以\((6，6)\)为例子，推广到\(n\)后就是 $ \large C_{2n}^{n} - C_{2n}^{n-1}$

四、公式推导变形

\[\large C_{2n}^{n}-C_{2n}^{n-1}=\frac{(2n)!}{n! \times n!}-\frac{(2n)!}{(n+1)!\times (n-1)!} \\ =\frac{(2n)!\times (n+1)}{n!\times (n+1)!}-\frac{(2n)!\times n}{n! \times (n+1)!} \\ =\frac{(2n)!\times (n+1)-(2n)!\times n}{n!\times (n+1)!} \\ =\frac{(2n)!}{n!\times (n+1)!}=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!} =\frac{C_{2n}^n}{n+1} \]

五、取模怎么办？

$ \large C_{2n}^{n} - C_{2n}^{n-1}= \frac{C_{2n}^{n}}{n+1} = \frac{2n \times (2n-1) \times ... \times (n+1) }{n \times (n-1) \times (n-2) \times ... \times 1} \ mod (m) \times inv(n+1)$

$ = 2n \times (2n-1) \times ... \times (n+1) \times inv(n+1) \times inv(n) \times inv(n-1) \times inv(n-2) \times ... \ mod(m)$

六、总结

需要注意的是，由于卡特兰数增长速度较快，当 \(n\) 等于 \(17\) 时，卡特兰数将会超过 \(int\) 最大值，造成溢出。对于 \(C++\) 语言来说，可以使用 高精度 来计算大整数。

七、实现代码

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int p = 1e9 + 7;
int n;

int qmi(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = (LL)res * a % p;
        b >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}

int main() {
    cin >> n;
    int res = 1;

    // ① 分子,2n*(2n-1)*(2n-2)*...*(n+1)
    for (int i = 2 * n; i > n; i--) res = (LL)res * i % p;
    // ② 分母,inv(n+1)*inv(n)*inv(n-1)*...*inv(1) %p
    for (int i = n + 1; i; i--) res = (LL)res * qmi(i, p - 2) % p;
    // 输出
    cout << res << endl;
    return 0;
}

八、牛刀小试

比如\(2016\)年全国三卷数学选择题压轴题让求解的就是卡特兰数，问题如下：

卡特兰数结论：

\[\large \frac{C_{2n}^n}{n+1} \]

题目结果:

\[\large \frac{C_{2m}^{m}}{m+1}=\frac{C_8^4}{4+1}=\frac{70}{5}=14 \]

因此选择\(C\)。