AcWing 883. 高斯消元解线性方程组

$AcWing$ $883$. 高斯消元解线性方程组

一、题目描述

输入一个包含 $n$ 个方程 $n$ 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 $m$ 个方程 $n$ 个未知数的线性方程组示例：

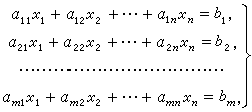
输入格式
第一行包含整数 $n$。

接下来 $n$ 行，每行包含 $n+1$ 个实数，表示一个方程的 $n$ 个系数以及等号右侧的常数。

输出格式
如果给定线性方程组存在唯一解，则输出共 $n$ 行，其中第 $i$ 行输出第 $i$ 个未知数的解，结果保留两位小数。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围
$1≤n≤100$,所有输入系数以及常数均保留两位小数，绝对值均不超过 $100$。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

二、线性方程组知识

三、高斯消元法

求解线性方程组的办法，是高斯消元法:

• 通过一系列的加减消元，得到类似 $kx=b$ 的式子，求得最后一个未知量的结果

• 然后逐一回代求解 整个 $x$ 向量

以下列方程为例：

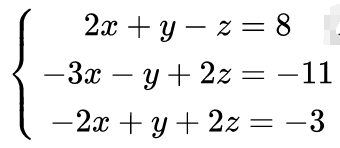
第一次加减消元，用第$1$式子消去后面所有的$x$得到：

方法：第$①$式左右两边除以$2$,然后左右两边乘以$②,③$式中$x$的系数,再分别加(减)到$②,③$式中,我称之为系数清零消元法

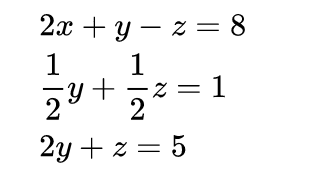
第二次加减消元，用第$2$个式子消去后面所有的$y$得到：

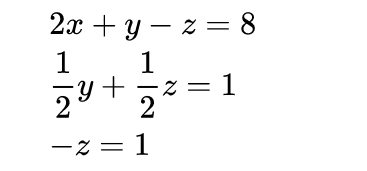
这样就完成了高斯消元的步骤$1$，形成了一个倒三角形的形状，接下来逐一回代即可。

用矩阵表示高斯消元

（1）消元过程：

（2）无解： 当消元完毕后，发现有一行系数都为 $0$，但是常数项不为 $0$，此时无解

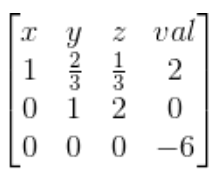
（3）多解： 当消元完毕后，发现有多行系数、常数项均为 $0$，此时多解，有几行为全为 $0$，就有几个自由元，即变量的值可以任取，有无数种情况可以满足给出的方程组

此时自由元为$2$个

常见问题

问题一: 为什么化简为 $1$的操作，和清零的操作都要倒着推?

当然也可以正着推，不过要用一个变量来记录一下开头的元素的值。化简都除以这个值就行了,不过有点麻烦，倒着推时要以省一个变量~

问题二：if (abs(a[t][c]) < eps) continue;如何理解?

假设 $c$表示列，$r$表示行，此时我们进行到了 $c=2$ $r=2$

1 0 2 3
0 0 3 2
0 0 2 3

你会发现此时$r$行之下 的$c$列的绝对值最大值就是$0$.
说明此时的第$c$列已经化简好了，那么不需要再进行后面的化简操作，
但是此时第$r$行不用变，此时$c$加$1$ 就接着从 第二行 第三列 开始找绝对值最大的数。
如果我们的$r$向后移动了，那么此时我们的第$2$行是没有化简的，这显然是不对的。
以此为例，$r$如果向后移动了，此时$r=3,c=3$但是此时我们的 第二行 第三列 是 $3$ 并不是$1$这种最简的形态。

问题三：倒着推解是如何来的

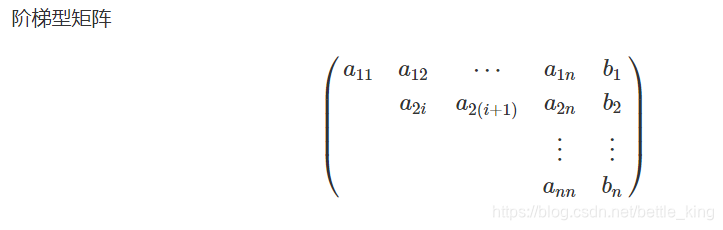
当有唯一解的时候，我们最后的化简一定是这种。
解的最终形式，如下所示:

我们倒着将每一行都简成每一行只有一个$1$ 的形式。 这里模拟一下，代码就懂了。

5、手绘流程

$Code$ 下标从$1$开始 【推荐】

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                    // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 1;                                                   // 先按行后按列进行计算，当前行是第1行
    for (int c = 1; c <= n; c++) {                               // 枚举每一列
        int t = r;                                               // 防破坏r,复制出t
        for (int i = r; i <= n; i++)                             // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;              // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                        // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n + 1; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n + 1; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i <= n; i++)                         // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n + 1; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                    // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                     // 下一行
    }
    if (r <= n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i <= n; i++)
            if (abs(a[i][n + 1]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                                 // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 1; i; i--)                   // 行,倒序
        for (int j = i + 1; j <= n; j++)          // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n + 1] -= a[i][j] * a[j][n + 1]; // 系数消为0
    return 1;                                     // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)         // n个方程
        for (int j = 1; j <= n + 1; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0)
        puts("No solution");
    else if (t == 2)
        puts("Infinite group solutions");
    else
        for (int i = 1; i <= n; i++) printf("%.2lf\n", a[i][n + 1]); // 保留两位小数
    return 0;
}

$Code$ 下标从$0$开始【不推荐】

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 0;                                               // 先按行后按列进行计算，当前行是第1行
    for (int c = 0; c < n; c++) {                            // 枚举每一列
        int t = r;                                           // 防破坏r,复制出t
        for (int i = r; i < n; i++)                          // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;          // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                    // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i < n; i++)                      // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                 // 下一行
    }
    if (r < n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i < n; i++)
            if (abs(a[i][n]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                             // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 2; i >= 0; i--)      // 行,倒序
        for (int j = i + 1; j < n; j++)   // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n] -= a[i][j] * a[j][n]; // 系数消为0
    return 1;                             // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++)      // n个方程
        for (int j = 0; j <= n; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0)
        puts("No solution");
    else if (t == 2)
        puts("Infinite group solutions");
    else
        for (int i = 0; i < n; i++) printf("%.2lf\n", a[i][n]); // 保留两位小数
    return 0;
}

五. 经验教训

练习题：$P3389$ 【模板】高斯消元法
1、一定要复制题目中输出的字符串，我就是因为No Solution -> No solution挂了第一个点
2、$Luogu$的模板题中，没有强制区分无解和无穷多组解。

#include <bits/stdc++.h>
using namespace std;

const int N = 110;
const double eps = 1e-8; // 小数的精度值
int n;                   // n个方程
double a[N][N];          // 系数+结果矩阵

int gauss() {                                                    // 高斯消元，答案存于a[i][n]中，0 <= i < n
    int r = 1;                                                   // 先按行后按列进行计算，当前行是第1行
    for (int c = 1; c <= n; c++) {                               // 枚举每一列
        int t = r;                                               // 防破坏r,复制出t
        for (int i = r; i <= n; i++)                             // 当前行需要找它的后续行
            if (abs(a[i][c]) > abs(a[t][c])) t = i;              // t的任务是找出c列中系数最大值是哪一行
        if (abs(a[t][c]) < eps) continue;                        // 如果c列绝对值最大的系数是0, 那么处理下一列
        for (int i = c; i <= n + 1; i++) swap(a[t][i], a[r][i]); // 将绝对值最大的行与当前行交换
        for (int i = n + 1; i >= c; i--) a[r][i] /= a[r][c];     // a[r][c]:行首系数，将当前行的行首通过除法变为1,倒序
        for (int i = r + 1; i <= n; i++)                         // 用当前行r的c列，通过减法将后续行c列消成0
            for (int j = n + 1; j >= c; j--)                     // 倒序,需要保留行首，逻辑和上面是一样的，行首值是变更系数，如果正序就把系数变成1了，后面就不对了
                a[i][j] -= a[r][j] * a[i][c];                    // a[i][c]:需要变化的乘法系数，减法：对位相消
        r++;                                                     // 下一行
    }
    if (r <= n) { // 如果没有成功执行完所有行，意味着中间存在continue,也就是某一列的系数都是0
        for (int i = r; i <= n; i++)
            if (abs(a[i][n + 1]) > eps) return 0; // 系数是0，但结果不是0，无解
        return 2;                                 // 系数是0，结果也是0，x取啥都对，有无穷多组解
    }
    // 代回求每个变量值
    for (int i = n - 1; i; i--)                   // 行,倒序
        for (int j = i + 1; j <= n; j++)          // 列,倒三角,右上角应该都是0,对角线全是1
            a[i][n + 1] -= a[i][j] * a[j][n + 1]; // 系数消为0
    return 1;                                     // 有唯一解
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)         // n个方程
        for (int j = 1; j <= n + 1; j++) // 每行n+1个数据，因为最后一列是等号右侧值
            cin >> a[i][j];

    int t = gauss();
    if (t == 0 || t==2)
        puts("No Solution");
    else
        for (int i = 1; i <= n; i++) printf("%.2lf\n", a[i][n + 1]); // 保留两位小数
    return 0;
}